И жесткость.
Задается: схема нагружения вала (рис. 7), длины участков вала: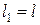 
; 
; 
; 
; 
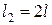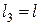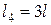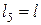, величины распределенных моментов: 
; 
; 
; 
; 
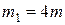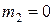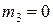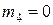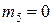, величины сосредоточенных моментов: 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
.
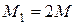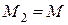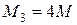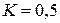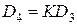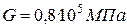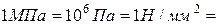
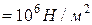Требуется:
1) построить эпюру крутящих моментов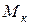 
;
2) из расчета на прочность, приняв 
, определить размеры поперечных сечений бруса;
3) построить эпюру касательных напряжений 
;
4) построить эпюру углов закручивания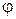 
;
5) произвести проверку условия жесткости на отдельных участках вала (при невыполнении условия жесткости подобрать соответствующие размеры из последнего);
6) выполнить эскиз вала в соответствии с назначенными размерами.
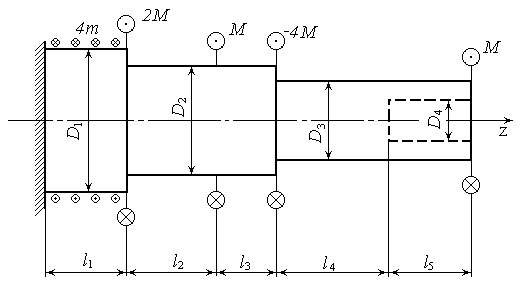
Рис. 7. Схема нагружения вала
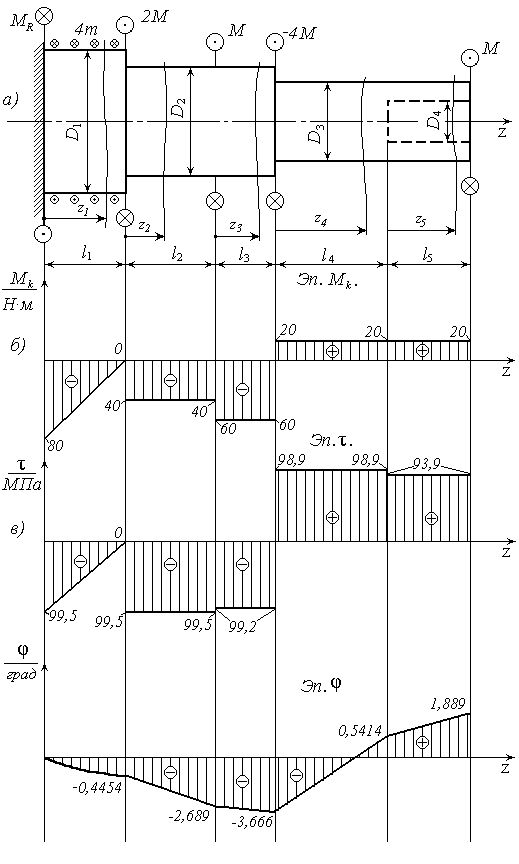
Рис. 8. Расчетная схема вала, эпюры крутящих моментов, касательных напряжений и углов закручивания
РЕШЕНИЕ
1. Определение реактивного момента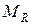 
в заделке (рис. 8,а).
Для определения реактивного момента составляется уравнение равновесия вала:
.
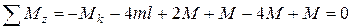Учитывая, что , определяется реактивный момент:
.
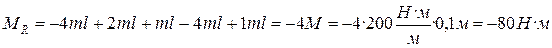2. Разбивка вала на участки.
Для построения эпюры крутящих моментов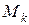 
по длине вала необходимо рассмотреть пять участков с координатами: 
, 
, 
, 
, 
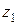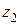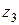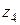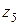(рис. 8,а).
3. Определение законов изменения крутящего момента по участкам вала.
3.1. Первый участок (рис. 9).
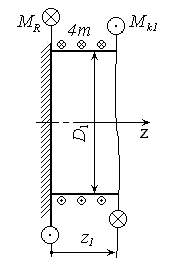
Рис. 9. К определению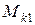 
на первом участке
Координата 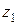для первого участка изменяется в пределах 
.
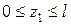Уравнение равновесия для отсеченной (левой) части вала имеет вид:
; 
.
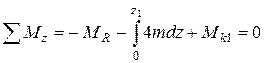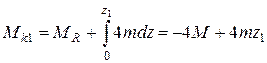Крутящий момент на границах участка принимает значения:
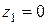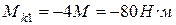при 
; 
, при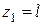 
; 
.
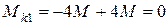3.2. Второй участок (рис. 10).
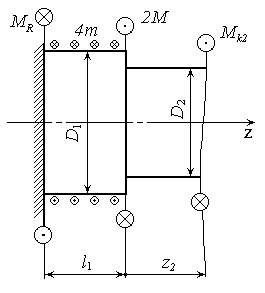
Рис. 10. К определению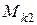 
на втором участке
На втором участке координата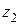 
изменяется в пределах 
.
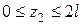Уравнение равновесия для отсеченной части вала записывается в виде:
,
.
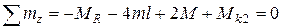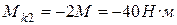На втором участке крутящий момент постоянен по длине участка и равен .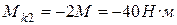
3.3. Третий участок (рис. 11).
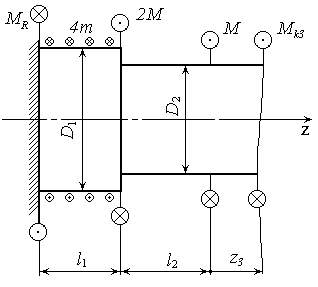
Рис. 11. К определению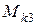 
на третьем участке
Координата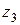 
для третьего участка изменяется в пределах 
.
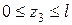Уравнение равновесия для отсеченной части вала и значения крутящего момента в граничных сечениях участка соответственно равны:
.
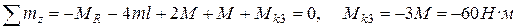На третьем участке крутящий момент постоянен по длине участка и равен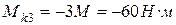 
.
3.4. Четвертый участок (рис. 12).
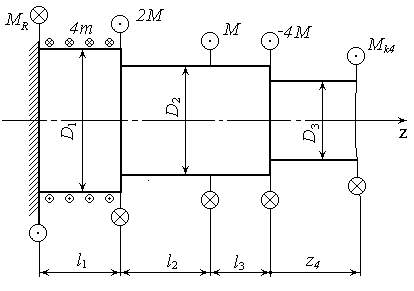
Рис. 12. К определению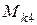 
на четвертом участке
Координата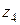 
для третьего участка изменяется в пределах 
.
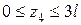Уравнение равновесия для отсеченной части вала и значения крутящего момента в граничных сечениях участка соответственно равны:
.
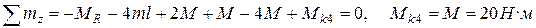На третьем участке крутящий момент постоянен по длине участка и равен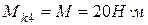 
.
3.5. Пятый участок (рис. 13).
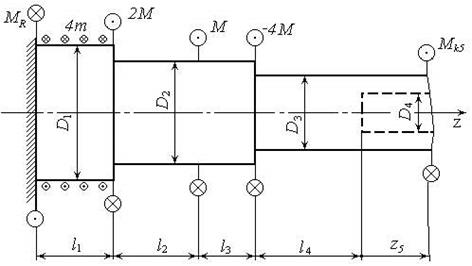
Рис. 13. К определению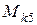 
на пятом участке
Координата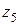 
на пятом участке изменяется в пределах 
.
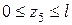Уравнение равновесия для отсеченной (левой) части вала имеет вид:
.
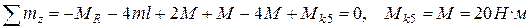На пятом участке крутящий момент постоянен по длине участка и равен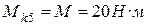 
.
4. Из условия прочности определяем размеры поперечных сечений бруса (приняв ).
.
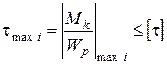4.1. Первый участок:
; 
;
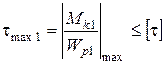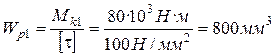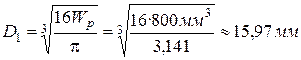. Примем 
.
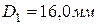4.2. Второй участок:
; 
,
.
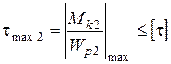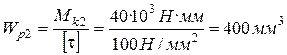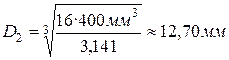4.3. Третий участок:
; 
,
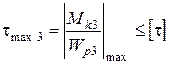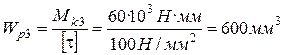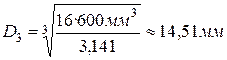. Примем 
.
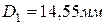4.4. Четвертый участок:
; 
,
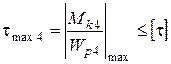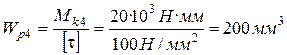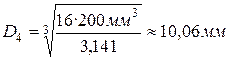. Примем 
.
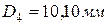4.5. Пятый участок:
; 
,
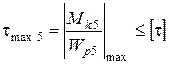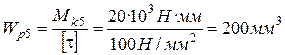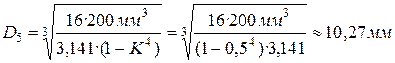. Примем 
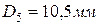, следовательно 
.
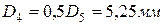5. Определение закона изменения касательного напряжения по участкам вала.
5.1. На первом участке закон изменения касательного напряжения в соответствии с формулой (3) имеет вид:
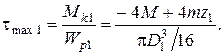
Касательное напряжение линейно зависит от координаты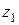 
и на границах участка принимает значения:
при ;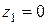 
;
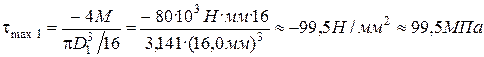при ;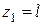 
.
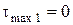5.2. На втором участке касательное напряжение на границах участка принимает значения:
.
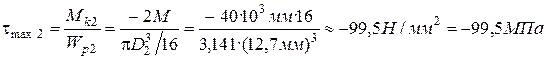5.3. На третьем участке касательное напряжение равно:
.
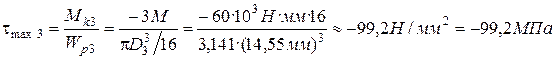5.4. Касательное напряжение на четвертом участке равно:
.
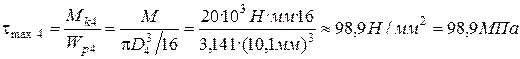5.5. На пятом участке касательное напряжение равно:
.
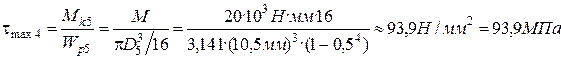По результатам вычислений строится эпюра касательных напряжений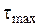 
(рис.8, в).
6. Определение закона изменения углов закручивания на участках вала.
6.1. На первом участке угол закручивания в соответствии с законом Р. Гука равен:
.
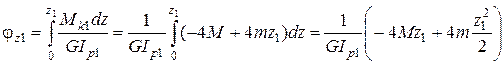Угол закручивания изменяется по кривой второго порядка и на границах участка принимает значения:
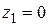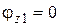при 
; 
, при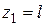 
; 
.
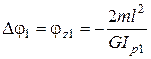Определим выпуклость кривой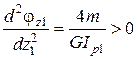 
, следовательно, кривая 
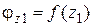выпукла вниз.
Условие экстремума кривой –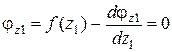 
,
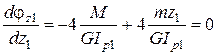, следовательно, функция 
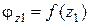имеет экстремум на границе участка при .
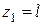Вычислим угол закручивания при :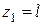
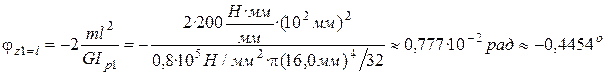
6.2. На втором участке угол закручивания равен:
;
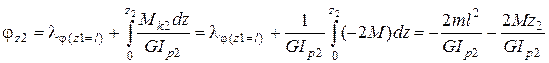при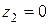 
; 
,
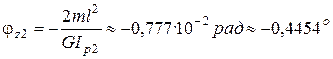при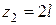 
; 
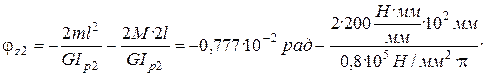
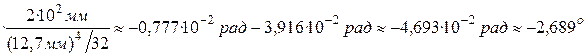
6.3. На третьем участке угол закручивания равен:
;
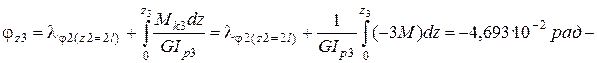
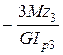при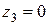 
; 
;
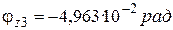при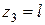 
; 
.
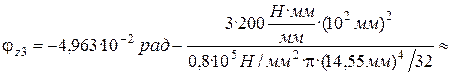
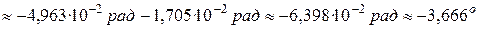6.4. На четвертом участке угол закручивания равен:
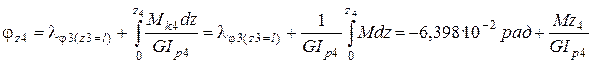
при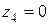 
; 
;
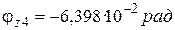при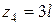 
; 
.
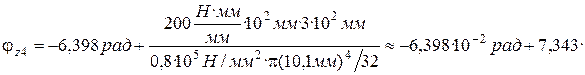
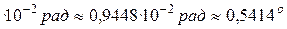6.5. На пятом участке угол закручивания равен:
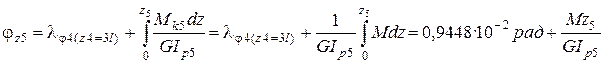при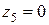 
; 
;
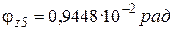при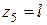 
; 
.
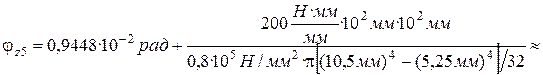
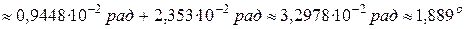7. Выполняется проверка условия жесткости на каждом участке вала. Условие жесткости имеет вид:
,
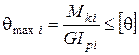где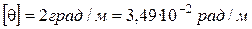 
.
;
;
;
;
.
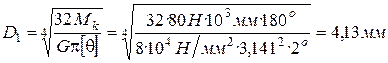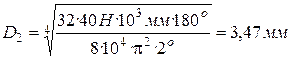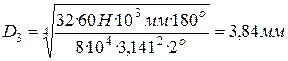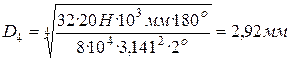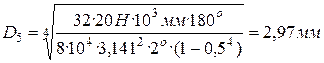Так как размеры сечений бруса, выбранные из условия жесткости меньше, чем размеры, выбранные из условия прочности, то принимаются такие размеры, которые будут удовлетворять условию прочности.
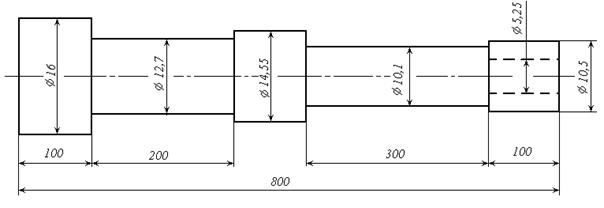
Рис. 14. Эскиз проектируемого вала
Вопросы и задания для самопроверки
1. При каком нагружении брус испытывает деформацию кручения?
2. Что называется валом?
3. Какое правило знаков принято для крутящих моментов?
4. Какие напряжения возникают в поперечных сечениях вала круглого сечения при кручении? Закон его распределения по высоте сечения вала?
5. Как записывается условие прочности при кручении?
6. Напишите выражения полярных моментов инерции и полярных моментов сопротивления круглого (сплошного и кольцевого) сечения.
7. Как выбираются допускаемые напряжения при кручении?
8. Как записываются условия жесткости при кручении?
9. Что называется жесткостью сечения вала?
10. Приведите примеры реальных конструкций, работающих в условиях кручения, применительно к вашей специальности.
ВАРИАНТЫ РАСЧЕТНО-ПРОЕКТИРОВОЧНОЙ РАБОТЫ
