Цель работы: разработка мероприятий по контролю качества продукции.
Теоретическая часть
Федеральный институт качества (США) при разработке мероприятий по контролю качества рекомендует выполнять следующие действия.
1. Создать образ организации через 3-5 лет.
2. Предложить принципы организации, соответствующие образу, то есть характеристики, на основе которых в организации будут приниматься ключевые решения.
3. Создать рабочую группу, которая будет направлять усилия по повышению качества.
4. Разработать план по осуществлению контроля качества на местах. При этом продумать:
· способы определения превалирующих норм, ценностей и убеждений, потенциальных барьеров и движущих сил в процессе борьбы за качество;
· возможности наделения полномочиями рядовых работников и обеспечения входящей информации по основным вопросам;
· методы оценки и вознаграждения за вклад в достижение целей организации, связанных с качеством;
· пути воспитания чувства локтя и духа соперничества среди работников, между начальниками и подчиненными;
· возможности получения работниками необходимых знаний, постоянного совершенствования;
· направления сбора информации о клиентах, их потребностях и степени их удовлетворенности;
· способы определения и анализа основных процессов;
· пути создания команд и освоения инструментарии для решения возникающих вопросов.
Практическая часть
Студенты разрабатывают мероприятия по контролю качества продукции на машиностроительных предприятиях с учетом предложенных рекомендаций.
Выводы
В выводах обосновываются предлагаемые мероприятия.
Контрольные вопросы
1. На чем акцентирует внимание при разработке мероприятий по контролю качества Федеральный институт качества США?
2. Сравните программы качества США и Японии.
3. Как согласуются мероприятия по контролю качества Федерального института качества США с принципами TQM?
Практическая работа № 7
ПРИЕМОЧНЫЙ КОНТРОЛЬ ПРОДУКЦИИ ПО АЛЬТЕРНАТИВНОМУ ПРИЗНАКУ
Цели работы:
1. Построить кривые вероятности приемки (КВП). По КВП при заданных значениях риска поставщика и риска потребителя определить величину приемлемого уровня дефектности и бракуемого уровня дефектности.
2. Построить кривые среднего уровня выходной дефектности (КСУВД) и определить его максимальные значения.
Теоретическая часть
1. Как известно из курса теории вероятностей, вероятность обнаружить d дефектных изделий в выборке объема n, взятой из партии в N изделий, среди которых D дефектных, равна
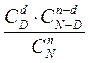 |
(1)
Поэтому партия будет принята с вероятностью P(q), равной сумме величин (1), где суммирование ведется для d = 0.1,…, c. Выражение (1) может быть приближенно вычислено с помощью распределения Пуассона и, следовательно
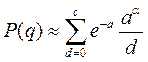 |
, (2)
где a = n W.
Эти значения содержатся в таблице 2 для различных c и a. Соотношение q = W . 100 легко позволяет получить формулу q = a/n . 100.
1. Критерием принятия решения при контроле является число дефектных изделий d в выборке:
при d £ c партию принимают;
при d > c партию бракуют.
Однако потребитель может требовать, чтобы партия с высоким уровнем входной дефектности могла пройти процедуру контроля и быть принятой лишь с малой вероятностью (не большей числа b). Аналогично поставщик заинтересован, чтобы достаточно "хорошие" партии (с небольшим q) браковались при контроле только с малой вероятностью (не большей, чем a). В этом случае на основании КВП как раз и найдены те значения qa и qb, которые гарантируются данной процедурой контроля:
потребителю гарантируется, что вероятность того, что в принятой партии уровень дефектности превосходит qb - меньше b;
поставщику гарантируется, что если уровень входной дефектности не превышает qa, то такая партия может быть забракована с вероятностью не большей, чем a.
2. С вероятностью, определяемой формулой (2), партия, имеющая уровень входной дефектности q, будет принята. При этом потребитель получит (D - d) дефектных деталей. Выходную дефектность (по аналогии с входной) определяют соотношением
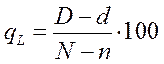 |
Математическое ожидание этой случайной переменной будет равно
 |
(3)
но при n много меньше, чем N, полагают
 |
и тогда
 |
откуда следует формула (2).
Очевидно, практический интерес представляет максимальное значение, которое может принимать qL и которое находится при помощи кривой среднего уровня выходной дефектности (КСУВД).
Практическая часть
В работе используются обозначения:
1. Известные величины:
N - число изделий каждой партии, предъявляемой на контроль;
n - объем выборки (число контролируемых изделий) n < N;
d - число дефектных изделий, обнаруженных в выборке при контроле;
c -приемочное число:
партия принимается, если d £ c, и бракуется, если d > c
a - риск поставщика (максимально допустимая вероятность браковки партии с низкой дефектностью);
b - риск потребителя (максимально допустимая вероятность приемки партии с высоким уровнем дефектности).
2. Неизвестные величины:
D - число дефектных изделий во всей контролируемой партий;
W = D/N - - доля дефектных изделий в партии;
q= W . 100 - дефектность (входная) партии, %
qa - приемлемый уровень входной дефектности, %;
qb - бракуемый уровень входной дефектности, %;
a = n W - среднее число дефектных изделий в выборке;
P (q) - вероятность приемки партии, имеющей входную дефектность q;
qL - средняя выходная дефектность в принятых партиях, т.е. математическое ожидание невыявленной дефектности в партиях, успешно прошедших процедуру контроля.
Работа выполняется индивидуально каждым студентом (бригадой 2-3 человека) по вариантам заданий, представленным в табл. 1.
Таблица 1
Варианты заданий
| Номер варианта | Приемочное число c | Объем выборки n | Риск поставщика a | Риск потребителя b |
| 0,10 | 0,05 | |||
| 0,05 | 0,10 | |||
| 0,05 | 0,05 | |||
| 0,10 | 0,10 | |||
| 0,05 | 0,10 | |||
| 0,10 | 0.05 | |||
| 0,05 | 0,10 | |||
| 0,10 | 0,10 | |||
| 0,05 | 0,05 | |||
| 0,05 | 0,05 |
1. Построение КВП заключается в графическом изображении функциональной зависимости вероятности Р приемки партии от входной дефектности q: Р = f(q)
1.1. 3начения P при заданном приемочном числе c выбирается через желаемый интервал из табл.2.
Таблица 2
Значения P в зависимости от приемочного числа c для различного среднего числа дефектных изделий в выборке a = n W
| Среднее число дефектных изделий в выборке a = n W | Приемочное число c, равное | ||||
| 0,0 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
| 0,05 | 0,95 | 1,00 | 1,00 | 1,00 | 1,00 |
| 0,10 | 0,90 | 0,99 | 1,00 | 1,00 | 1,00 |
| 0,20 | 0,82 | 0,98 | 1,00 | 1,00 | 1,00 |
| 0,30 | 0,74 | 0,96 | 1,00 | 1,00 | 1,00 |
| 0,50 | 0,61 | 0,91 | 0,99 | 1,00 | 1,00 |
| 1,00 | 0,37 | 0,74 | 0,92 | 0,98 | 1,00 |
| 2,00 | 0,14 | 0,41 | 0,68 | 0,86 | 0,95 |
| 3,00 | 0,05 | 0,20 | 0,42 | 0,65 | 0,82 |
| 4,00 | 0,02 | 0,09 | 0,24 | 0,43 | 0,63 |
| 5,00 | 0,01 | 0,04 | 0,12 | 0,26 | 0,44 |
| 8,00 | 0,00 | 0,00 | 0,01 | 0,04 | 0,1 |
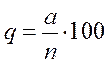 |
1.2. По таблице 2 для соответствующего значения P при заданном c определяется a (среднее число дефектных изделий в выборке), откуда по формуле
находится q. В таблице 3 представлен пример расчетов для c =1 и n =50. Данные по величинам N, d, D задаются преподавателем.
Таблица 3
Данные для расчета величины входной дефектности партии q при
c = 1 и n = 50
| P | 1,00 | 0,96 | 0,74 | 0,41 | 0,20 | 0,09 | 0,04 |
| a = n W | 0,0 | 0,3 | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 |
| q, % | 0,0 | 0,6 | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 |
1.3. По заполненной таблице (аналогичной таблице 3) строится КВП. Примерный вид КВП изображен на рис. 1, где P = f(q).

Рис.1. Кривая вероятности приемки партии при c = 1 и n = 50.






