37. Алгебраїчні конгруенції другого степеня.
Конгруенція 
, 
називається квадратною конгруенцією за модулем 
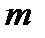. Число 
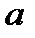називається квадратичним лишком за модулем 
, якщо конгруенція 
має розв’язки. Число 
називається квадратичним нелишком за модулем 
, якщо конгруенція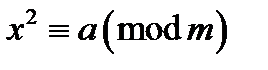 
розв’язків не має.
Якщо число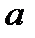 
є квадратичним лишком за модулем 
, то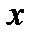 
називається квадратним коренем з числа 
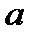за модулем 
.
Задача знаходження розв’язків квадратичної конгруенції має важливе значення в криптографії.
Виявляється, що у загальному випадку не тільки ця задача, а навіть питання про розв’язуваність квадратичної конгруенції за модулем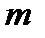 
, який є складеним числом, факторизація якого невідома, є нерозв'язною проблемою. Але для модулів, які є простими числами, ця проблема досить легко розв’язується.
Теорема 1. Якщо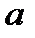 
– квадратичний лишок за модулем 
, то конгруенція 
, 
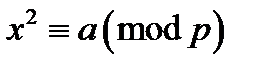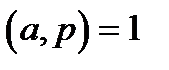, має два розв’язки.
Теорема 2. Зведена система лишків за простим модулем 
складається з 
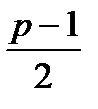квадратичних лишків, конгруентних числам 
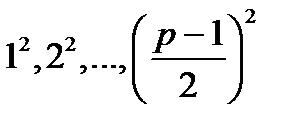і 
квадратичних нелишків.
У разі простого модуля 
питання про наявність розв’язків конгруенції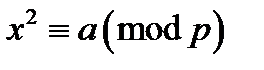 
, 
, можна з’ясувати за допомогою наступного критерію Ейлера.
Теорема. (критерій Ейлера для визначення квадратичних лишків і нелишків). Нехай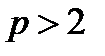 
– просте непарне число. Число 
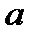, взаємно просте з 
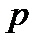, буде квадратичним лишком за модулем 
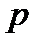тоді і тільки тоді, коли 
, і буде квадратичним нелишком за модулем 
тоді і тільки тоді, коли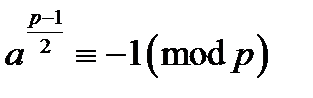 
.
38. Символи Лежандра і Якобі.
Існують алгоритми для визначення, чи є дане число квадратичним лишком за простим модулем чи ні. Один з алгоритмів позв'язаний з обчисленням значення символу Лежандра, якій для непарного простого 
визначається так:
Значення 
називається квадратичним характером числа 
за простим модулем 
.
Основні властивості символу Лежандра.
1) 
;
2) Критерій Ейлера: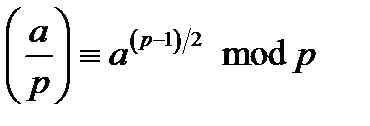 
;
3) 
;
4) 
;
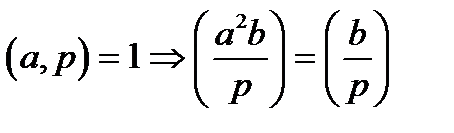5) 
, 
;
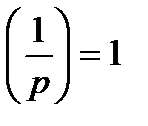6) 
.
7) Квадратичний закон взаємності Гаусса: для будь-яких простих непарних чисел 
і 
виконується рівність 
.
Символ Лежандра 
можна обчислити за допомогою наступної послідовності дій. (1) Якщо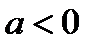 
, те виділяємо співмножник 
;
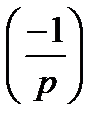(2) приводимо 
за модулем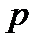 
;
(3) розкладаємо 
в добуток ступенів простих чисел, використовуючи мультипликативность символу Лежандра: 
, потім видаляємо співмножники які є квадратами;
(4) виділяємо двійки, наприклад, якщо 
, обчислюємо 
;
(5) для кожного непарного співмножника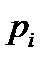 
застосовуємо квадратичний закон взаємності (зменшуємо величини чисел, що беруть участь в обчисленнях,);
(6) при необхідності переходимо до п.(1).
Приклад. 
.
Символ Якобі числа 
за модулем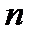 
, при 
, визначається як добуток значень символів Лежандра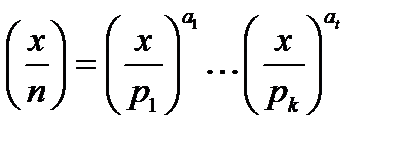 
.
Символ Якобі має практично всі ті ж властивості, що і символ Лежандра, але за значенням символу Якобі, рівному одиниці, не можна стверджувати, що відповідний лишок – квадратичний.
Для квадратичного лишку символ Якобі, проте, дорівнює одиниці. Отже, коли 
, то 
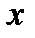– квадратичний нелишок за модулем 
.
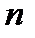39. Добування квадратного кореня за простим модулем.
Даний алгоритм призначений для розв’язання відносно 
порівняння виду 
за простим модулем 
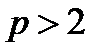. Перед тим як приступити до обчислень, необхідно переконатися внаявності розв'язків порівняння, тобто в тім, що 
.
Алгоритм розбивається на 3 випадки, в залежності від представлення 
у виді 
, 
, 
. В алгоритмі істотно використовується критерій Ейлера, який для розв'язного порівняння дає: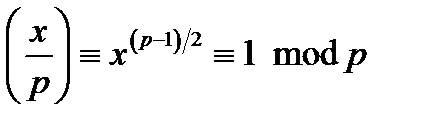 
.
Випадок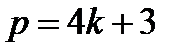 
. Маємо 
. Помножимо на 
ліву і праву частину порівняння, одержимо: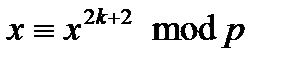 
. Показник праворуч парний, отже, одне з рішень 
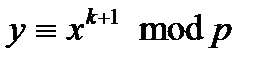. Оскільки рішень не може бути більш двох, те остаточна відповідь: 
.
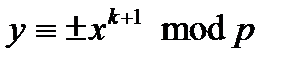Випадок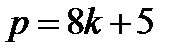 
. Оскільки 
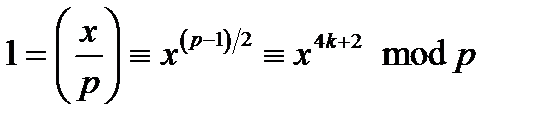, те 
.
Таким чином, вірно одне з двох співвідношень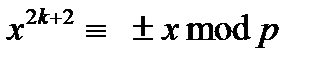 
. Оскільки 
і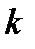 
відомі, то можна перевірити, яке зі співвідношень виконується. Таким чином, можливі наступні два підвипадки.
Якщо вірно 
, то, очевидно,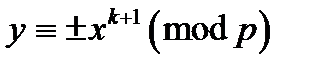 
. Інакше, 
.
Якщо обидві частини останнього порівняння помножити на число у відомому парному степені, то квадратний корінь з його лівої частини легко записати явно. Ми підберемо зазначений множник так, щоб, крім того, змінився знак у правої частини порівняння.
Таким множником може бути число 
, оскільки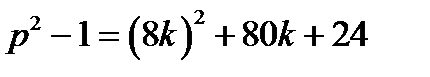 
. Отже, 
Випадок, 
. Насамперед, для роботи алгоритму необхідна наявність (довільного) квадратичного нелишку 
за модулем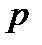 
. Щоб його знайти, приходиться вибирати навмання число, скажемо, 
і перевіряти співвідношення 
.
Уточнимо вигляд числа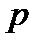 
: 
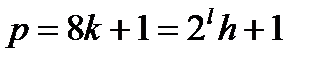, де 
- непарне, очевидно, 
.
Основна ідея алгоритму – побудувати співвідношення виду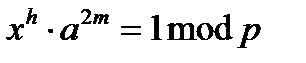 
.
У випадку успіху, досить помножити обидві частини порівняння на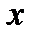 
і витягти корінь з обох частин (враховуючи, що число 
парне). Тому, виходячи з порівняння 
, ми будемо будувати співвідношення, у яких показник при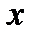 
буде знижуватися вдвічі, поки не стане рівним 
. Ділення показників на двійки це - послідовне здобуття квадратних коренів з одиниці. На кожнім кроці може з’явитися лише один з коренів: 1 або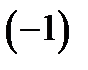 
. При цьому в нас буде досить даних, щоб з'ясувати, який випадок реально має місце. Змінювати знак у 
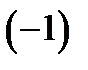ми будемо за допомогою множення частин порівняння на степені числа 
, причому так, щоб показник степеня в добутку таких додаткових множників завжди залишався парним.
