Відношення конгруентності записується у виді: 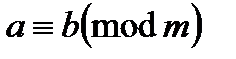 ,
,  ,
,  . Замість знака конгруентності часто використовується знак рівності. Числа, що мають однакові остачі від ділення на
. Замість знака конгруентності часто використовується знак рівності. Числа, що мають однакові остачі від ділення на  , конгруентні за модулем
, конгруентні за модулем  .
.
Стандартні значення лишків за модулем  належать множині
належать множині  (система найменших додатних лишків).
(система найменших додатних лишків).
Лишок суми за модулем  дорівнює сумі лишків, зведеної, якщо необхідно, ще раз за модулем
дорівнює сумі лишків, зведеної, якщо необхідно, ще раз за модулем  . Аналогічну властивість має лишок добутку.
. Аналогічну властивість має лишок добутку.
18. Кільце класів лишків.
Відношення конгруентності дозволяє розбити множину  цілих чисел на класи. Елементи одного класу мають однакові лишки за модулем
цілих чисел на класи. Елементи одного класу мають однакові лишки за модулем  . Очевидно, класи не перерізаються. Кожному класу відповідає один найменший додатний лишок і навпаки.
. Очевидно, класи не перерізаються. Кожному класу відповідає один найменший додатний лишок і навпаки.
Лишок суми або добутку за модулем  елементів
елементів  і
і  не залежить від вибору цих елементів, а залежить лише від вибору класів
не залежить від вибору цих елементів, а залежить лише від вибору класів  і
і  .
.
Можна побудувати кільце, елементами якого є класи, а операції виконуються через дії над відповідними найменшими додатними лишками.
Наприклад, якщо  , те клас, що містить
, те клас, що містить  , є множиною виду
, є множиною виду  . Оскільки множина
. Оскільки множина  цілих чисел є кільцем, то наша відповідність між класами і лишками
цілих чисел є кільцем, то наша відповідність між класами і лишками  є гомоморфізмом кілець. Образ цього гомоморфізму (кільце класів лишків за модулем
є гомоморфізмом кілець. Образ цього гомоморфізму (кільце класів лишків за модулем  ) називається фактором-кільцем кільця цілих чисел за модулем
) називається фактором-кільцем кільця цілих чисел за модулем  і звичайно позначається
і звичайно позначається  . Зауважимо, що нулем у кільці лишків у кільці
. Зауважимо, що нулем у кільці лишків у кільці  є клас
є клас  .
.
При зашифруванні інформації використовуються взаємно однозначні перетворення даних. Для знаходження обернених елементів у кільці  можна використовувати розширений алгоритм Евкліда
можна використовувати розширений алгоритм Евкліда
Алгоритм Евклида показує, що для взаємно простих чисел  і
і 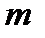 завжди існує число
завжди існує число  таке, що
таке, що  . Таке число називається оберненим до
. Таке число називається оберненим до  за модулем
за модулем  і позначається
і позначається  .
.
Дійсно, якщо  , то відносно
, то відносно  і
і  розв'язуване рівняння
розв'язуване рівняння  . Приводячи за модулем
. Приводячи за модулем  обидві частини зазначеної рівності, одержимо порівняння
обидві частини зазначеної рівності, одержимо порівняння  , тобто
, тобто  .
.
Якщо модуль є простим числом  , усі ненульові лишки за модулем
, усі ненульові лишки за модулем  взаємно прості з модулем. Отже, кільце
взаємно прості з модулем. Отже, кільце  .
.
19. Кільце класів лишків многочленів над полем.
За аналогією з кільцем лишків за модулем  , можна побудувати кільце лишків поліномів за модулем нормованого незвідного полінома
, можна побудувати кільце лишків поліномів за модулем нормованого незвідного полінома  над полем
над полем  .
.
Для цього досить розглянути множину залишків від ділення всіх поліномів із коефіцієнтами з  та помітити, що розширений алгоритм Евкліда може бути переформульований для розв’язування рівняння аналогічного
та помітити, що розширений алгоритм Евкліда може бути переформульований для розв’язування рівняння аналогічного  , а саме:
, а саме: 

 .
.
Якщо покласти  , то, при
, то, при  ,
, 
 і співвідношення
і співвідношення  , після зведення за модулем
, після зведення за модулем  дає
дає  . Тому всі ненульові елементи нашого кільця оборотні тобто воно є полем.
. Тому всі ненульові елементи нашого кільця оборотні тобто воно є полем.
Оскільки коефіцієнти поліномів обчислюються за правилами арифметики  , то число
, то число  є характеристикою нашого поля
є характеристикою нашого поля  . Очевидно, що кількість елементів
. Очевидно, що кількість елементів  поля
поля  дорівнює кількості поліномів, степеня меншої
дорівнює кількості поліномів, степеня меншої  .
.
Для визначення  зауважимо, що набору коефіцієнтів кожного полінома степеня меншого
зауважимо, що набору коефіцієнтів кожного полінома степеня меншого  , відповідає вектор, кількість координат якого дорівнює
, відповідає вектор, кількість координат якого дорівнює  . Кожна координата може приймати лишь значення
. Кожна координата може приймати лишь значення  . Отже,
. Отже,  . Таким чином,
. Таким чином,  .
.
Довільний вектор можна розглядати як набір коефіцієнтів деякого полінома. При цьому сумі поліномів буде відповідати сума зазначених векторів. Результатом добутку векторів є вектор коефіцієнтів залишку від ділення добутку поліномів на  .
.
У підсумку, елементи поля  можна розглядати як
можна розглядати як  - вимірні вектори з координатами з підполя
- вимірні вектори з координатами з підполя  .
.
Число  називається степенем розширення
називається степенем розширення  .
.
Елемент  поля
поля  представляється в поле
представляється в поле 
 - вимірним вектором (розширеним числом) виду
- вимірним вектором (розширеним числом) виду  .
.
20. Функція Ейлера та її властивості.
Порядки чисел за модулем  різні. Існують числа, що є порядком одночасно для всіх чисел, взаємно простих с.
різні. Існують числа, що є порядком одночасно для всіх чисел, взаємно простих с.  Одне з них дорівнює значенню функції Ейлера
Одне з них дорівнює значенню функції Ейлера  , що визначається як число чисел, взаємно простих з
, що визначається як число чисел, взаємно простих з  .
.
Функція Ейлера є мультиплікативною: якщо  , те
, те  і
і  .
.
Нехай 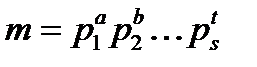 , тоді
, тоді  .
.
Число  називається первісним коренем (первісним елементом) за модулем
називається первісним коренем (первісним елементом) за модулем  , якщо його порядок за модулем
, якщо його порядок за модулем  дорівнює
дорівнює  .
.
При  первісні корені завжди існують.
первісні корені завжди існують.
Відомо, що в кожному скінченному полі також існує первісний елемент (генератор поля). Степені первісного елемента  представляють усі ненульові елементи поля.
представляють усі ненульові елементи поля.
Зокрема, якщо  первісний елемент поля
первісний елемент поля  , то конгруенція
, то конгруенція  розв'язувана для ненульових лишків
розв'язувана для ненульових лишків  за модулем
за модулем  .
.
Показник  у цій конгруенції називається дискретним логарифмом числа
у цій конгруенції називається дискретним логарифмом числа  за основою
за основою  . Дискретні логарифми часто називають індексами і позначають
. Дискретні логарифми часто називають індексами і позначають  або
або  .
.
21. Теореми Ейлера і Ферма.
Теорема Ейлера. Якщо  , то
, то  .
.
З теореми Ейлера випливає
Мала теорема Ферма:  , де
, де  - просте,
- просте,  .
.
Ці теореми інтенсивно використовуються в асиметричній криптографії і, крім того, дуже корисні для скорочення обчислень.
Як наслідок, з теореми Ейлера випливає, що елемент  є первісним коренем за модулем
є первісним коренем за модулем  тоді і тільки тоді, коли виконуються співвідношення:
тоді і тільки тоді, коли виконуються співвідношення:  , де
, де  .
.
Зауважимо, що в кожному скінченному полі  , при
, при  ,
,  , виконується співвідношення
, виконується співвідношення  . Це зв'язано з тим, що число
. Це зв'язано з тим, що число  є порядком мультиплікативної групи поля.
є порядком мультиплікативної групи поля.
Щоб врахувати значення  , помножимо обидві частини зазначеного співвідношення на
, помножимо обидві частини зазначеного співвідношення на  . Одержимо, що для будь-якого елемента
. Одержимо, що для будь-якого елемента  кінцевого поля вірне співвідношення
кінцевого поля вірне співвідношення  .
.
Нагадаємо, що розширення скінченного поля може бути представлене як кільце лишків многочленів за модулем незвідного многочлена,  над простим полем:
над простим полем:  .
.
Для деяких незвідних многочленів послідовність  пробігає всі можливі лишки, тобто всі елементи поля. Такі многочлени називаються примітивними.
пробігає всі можливі лишки, тобто всі елементи поля. Такі многочлени називаються примітивними.
22. Лінійні конгруенції.
Конгруенції виду  можуть мати декілька розв’язків, мати єдиний розв’язок або не мати розв’язків взагалі.
можуть мати декілька розв’язків, мати єдиний розв’язок або не мати розв’язків взагалі.
Якщо  , то розв’язок єдиний:
, то розв’язок єдиний: 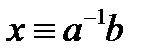 .
.
Відзначимо, що якщо модуль і коефіцієнти конгруенції  розділити або помножити як цілі числа на одне й те саме число, те отримана конгруенція буде істинною. Це випливає з того, що якщо
розділити або помножити як цілі числа на одне й те саме число, те отримана конгруенція буде істинною. Це випливає з того, що якщо  ділиться на
ділиться на  , а
, а  ділиться на
ділиться на  , те
, те  ділиться на
ділиться на  .
.
Теорема. Розв’язки конгруенції  існують тоді і тільки тоді, коли
існують тоді і тільки тоді, коли 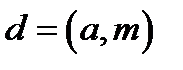 ділить
ділить  .
.
У цьому випадку, крім вихідної конгруенції, розв'язувані конгруенції виду 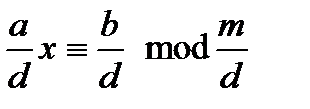 з єдиним розв’язком
з єдиним розв’язком  .
.
Очевидно, всі розв’язки вихідної конгруенції в діапазоні  є числами виду
є числами виду 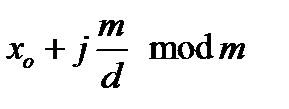 ,
,  .
.
Зокрема, якщо  просте, то конгруенція
просте, то конгруенція  має не більш одного розв’язку.
має не більш одного розв’язку.
23. Китайська теорема про остачі.
Нехай числа  попарно взаємно прості і
попарно взаємно прості і  . Тоді існує єдиний за модулем
. Тоді існує єдиний за модулем  розв’язок системи порівнянь
розв’язок системи порівнянь  ,
,  .
.
При цьому,  , де
, де  ,
,  .
.
Дійсно, у зазначеному вирзі для  , один доданок порівнянний з
, один доданок порівнянний з  за модулем
за модулем  , а всі інші порівнянні з нулем.
, а всі інші порівнянні з нулем.
Коефіцієнти  можна обчислити заздалегідь і розв’язувати кілька систем, підставляючи їхні праві частини в лінійну форму.
можна обчислити заздалегідь і розв’язувати кілька систем, підставляючи їхні праві частини в лінійну форму.
Китайська теорема про остачі показує, що розв’язок конгруенції  можна знайти, якщо знати розв’язки цієї конгруенції за модулями, рівними степеням простих чисел, що входять у канонічний розклад числа
можна знайти, якщо знати розв’язки цієї конгруенції за модулями, рівними степеням простих чисел, що входять у канонічний розклад числа  на співмножники.
на співмножники.






