53. Означення та властивості хеш-функцій, побудованих на однокрокових стискуючих функціях.
Означення. Хеш-функцією (hash-function) називається однонапрямлена функція 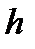 , яка відображає множину
, яка відображає множину  відкритих повідомлень в множину
відкритих повідомлень в множину  двійкових векторів фіксованої довжини:
двійкових векторів фіксованої довжини:  , і має наступні властивості:
, і має наступні властивості:
1) її значення достатньо легко обчислити, тобто знаючи відкрите повідомлення  , легко обчислити
, легко обчислити  ;
;
2) відновити відкрите повідомлення  за відомим значенням
за відомим значенням  неможливо протягом реального часу, тобто знаючи
неможливо протягом реального часу, тобто знаючи 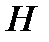 , важко визначити
, важко визначити  , для якого
, для якого  ;
;
3) знайти довільну пару відкритих повідомлень 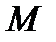 ,
,  ,
,  , таку, що
, таку, що  , неможливо протягом реального часу (подія, яка полягає в тому, що
, неможливо протягом реального часу (подія, яка полягає в тому, що  називається колізією).
називається колізією).
Значення хеш-функції для даного аргументу називається хеш-значенням, або хеш-кодом. Хеш-код, тобто образ повідомлення 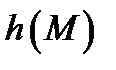 буде значно менше, ніж початкове повідомлення.
буде значно менше, ніж початкове повідомлення.
Однокрокові стискуючі функції є вектор-функціями від двох змінних вигляду 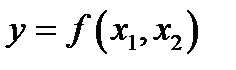 , де аргументи
, де аргументи 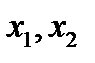 є двійковими векторами довжини
є двійковими векторами довжини  , а значення функції
, а значення функції  – двійковий вектор довжини
– двійковий вектор довжини  . Величина
. Величина  є довжиною хеш-коду.
є довжиною хеш-коду.
Для обчислення хеш-коду  повідомлення
повідомлення  розбивається на
розбивається на  блоків
блоків  довжини кратної
довжини кратної 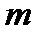 . Якщо довжина повідомлення
. Якщо довжина повідомлення  не кратна
не кратна 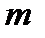 , то останній блок спеціальним способом доповнюють до довжини
, то останній блок спеціальним способом доповнюють до довжини  .До блоків
.До блоків  застосовують наступну послідовну процедуру обчислення хеш-коду:
застосовують наступну послідовну процедуру обчислення хеш-коду:
 ;
;
 ,
,  ;
;
 .
.
де  – деякий фіксований початковий вектор.
– деякий фіксований початковий вектор.
54. Типи криптографічних хеш-функцій.
Хеш-функції поділяються на два основних типи – ключові та безключові.
Для ключової хеш-функції, тобто такої, при обчисленні значень якої використовується додатковий секретний параметр, скажімо, 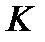 , значення її хеш-коду
, значення її хеш-коду  називається кодом аутентифікації повідомлення (імітовставкою) і має загальноприйняту абревіатуру МАС (message authentification code). Відповідні процедури обчислення значення ключової хеш-функції називаються алгоритмами обчислення коду аутентифікації повідомлення.
називається кодом аутентифікації повідомлення (імітовставкою) і має загальноприйняту абревіатуру МАС (message authentification code). Відповідні процедури обчислення значення ключової хеш-функції називаються алгоритмами обчислення коду аутентифікації повідомлення.
Основні вимоги до безключових хеш-функцій: односторонність, стійкість до колізій та складність заміни одного повідомлення з відомим хеш-кодом іншим повідомленням з тим самим хеш-кодом.
55. Принципи побудови та властивості генераторів псевдовипадкових чисел.
Генератор псевдовипадкових чисел (ГПВЧ) (Pseudorandom number generator, PRNG (англ.)) – алгоритм, що генерує послідовність чисел, якій характерні всі частотні (статистичні) властивості, типові для послідовності реалізацій якої-небудь випадкової величини із заданим законом розподілу. Найбільш поширені випадкові числа, які рівномірно розподілені на відрізку  .
.
Ці послідовності виходять за допомогою математичних алгоритмів із скінченним числом параметрів. Тому не кожен спосіб вибору елементів числової послідовності дає сукупність чисел з бажаними характеристиками.
При побудові генераторів ПВЧ висуваються лише необхідні вимоги до типів вибірок елементів, для яких статистичні властивості відповідають властивостям рівноймовірності і незалежності. Наприклад, можна зажадати, щоб розподіли будь-яких вибірок від одного до десяти чисел на відрізку послідовності не більше 100 практично не відрізнялися від випадкових.
Більшість простих арифметичних генераторів хоча і мають велику швидкість, але страждають від багатьох серйозних недоліків:
- Дуже короткий період/періоди;
- Послідовні значення не є незалежними;
- Деякі біти «менш випадкові», чим інші;
- Нерівномірний одновимірний розподіл;
- Оборотність.
Тому, в криптографії до псевдовипадкових послідовностей чисел висувають наступні вимоги:
1) Великий період;
2) Непередбачуваність зліва, тобто неможливість визначення члена 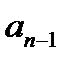 числової послідовності на основі її відомого наступного фрагменту
числової послідовності на основі її відомого наступного фрагменту  скінченної довжини
скінченної довжини  ;
;
3) Непередбачуваність справа, тобто неможливість визначення члена 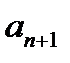 числової послідовності на основі її відомого попереднього фрагменту
числової послідовності на основі її відомого попереднього фрагменту 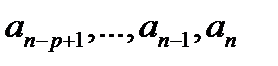 скінченної довжини
скінченної довжини  ;
;
56. Лінійні конгруентні генератори.
Найбільш відомий на сьогодні ГПВЧ являє собою окремі види алгоритму, який був запропонований Лехмером (Деррік Генрі Лехмер (1905–1991) – американський вчений, працював в університеті Беркли) ще у 1948 році і відомий як метод лінійного конгруента. Послідовність псевдовипадкових чисел  отримується за допомогою лінійного рекурентного рівняння
отримується за допомогою лінійного рекурентного рівняння
 (1)
(1)
де  – початкове значення (ключ);
– початкове значення (ключ);  – множник;
– множник;  – приріст;
– приріст; 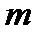 – модуль,
– модуль,  ,
,  ,
,  . Якщо
. Якщо  ,
, 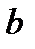 ,
,  – цілі числа, то утворюється послідовність цілих чисел в діапазоні
– цілі числа, то утворюється послідовність цілих чисел в діапазоні  .
.
Послідовність, що є розв’язком рівняння (1), називається лінійною конгруентною послідовністю.
57. Генератори псевдовипадкових чисел на основі однонапрямлених функцій з лазівкою. Генератор Блюма–Блюм–Шуба (ВВS).
Принцип роботи генератора BBS:
1. Навмання вибираються два великих псевдовипадкових простих числа  і
і  з властивістю
з властивістю  ,
,  та обчислюється ціле числом Блюма
та обчислюється ціле числом Блюма  . (числа
. (числа 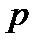 і
і  зберігаються у таємниці).
зберігаються у таємниці).
2. З мультиплікативної групи лишків  випадково вибирається інше ціле число
випадково вибирається інше ціле число  , взаємно просте з числом Блюма
, взаємно просте з числом Блюма  :
:  .
.
3. Обчислюється число 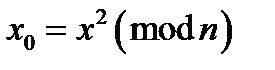 , яке буде початковим значенням генератора.
, яке буде початковим значенням генератора.
4. За законом 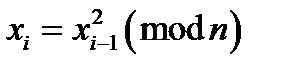 утворюється послідовність чисел
утворюється послідовність чисел 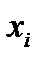 .
.
5. Шуканою псевдовипадковою двійковою послідовністю  буде послідовність молодших бітів чисел
буде послідовність молодших бітів чисел  , тобто
, тобто  ,
,  .
.
Псевдовипадкову двійкову послідовністю, згенеровану за цим алгоритмом, позначають як  .
.






