Елемент 
називається одиничним (або нейтральним) відносно розглянутої бінарної операції 
, якщо 
для усіх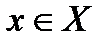 
. Якщо 
- ще один одиничний елемент, то 
.
Моноїдом називається напівгрупа 
з одиничним елементом 
.
Елемент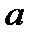 
моноида 
називається оборотним, якщо знайдеться елемент 
, для якого 
. Обернений до 
позначається через 
. Обернений елемент єдиний: 
. Запис операції у виді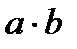 
називається мультиплікативною.
Групи
Моноїд, всі елементи якого оборотні, називається групою.
Аксіоми групи.
1. на множині 
визначена бінарна операція 
;
2. операція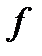 
асоціативна;
3. в множині 
відносно 
існує нейтральний елемент;
4. для кожного 
існує зворотний.
Кількість елементів скінченої групи називається її порядком.
Підмножина 
, групи 
називається підгрупою групи 
, якщо 
також є групою. Аналогічно визначаються підструктури інших алгебраїчних структур.
Теорема (Лагранж). Порядок скінченої групи ділиться на порядок будь-якої її підгрупи.
Група 
називається комутативною (абелевою) якщо 
. Абелевы групи виду 
називаються адитивними. Для 
запис 
позначає: 
. Аналогічним образом,: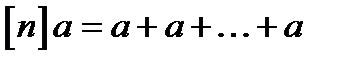 
.
Групи 
і 
гомоморфні, якщо існує відображення 
, таке, що 
. Відображення 
називається гомоморфізмом груп. Ядром гомоморфізму 
називається множина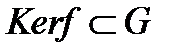 
, що є прообразом одиниці 
. Групи 
й 
ізоморфні, якщо існує гомоморфізм 
з 
у 
, причому відображення 
є взаємно однозначним. Відображення 
є автоморфізмом групи 
, якщо відображення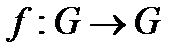 
- ізоморфізм. Відображення 
є эндоморфизмом групи 
, якщо відображення 
- гомоморфізм.
Кільця
Асоціативним кільцем називається множина 
з двома операціями, що називаються додаванням і множенням і для яких виконуються наступні аксіоми.
1.Ассоциативнось додавання: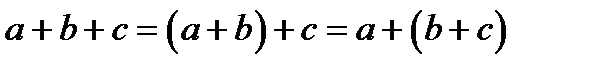 
.
2. Коммутативность додавання: 
.
3. Можливість розв'язання рівняння 
для усіх 
.
4. Ассоциативнось для множення: 
.
5. Дистрибутивность при множенні зліва: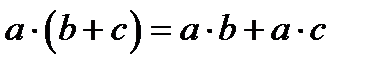 
.
6. Дистрибутивность при множенні зправа: 
.
Звичайно під назвою «кільце» розуміється асоціативне кільце.
Кільце називається неасоціативним, якщо операція множення не є асоціативною. Кільце називається комутативним, якщо коммутативна операція множення.
У кільці існує нуль - одиничний елемент відносно додавання. Одиничний елемент 
відносно множення, з властивістю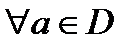 
, не обов'язково існує.
Прикладом комутативного кільця без одиниці є множина парних чисел зі звичайними операціями додавання і множення.
У кільці з одиницею можливе існування елемента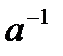 
, оберненого до елемента 
, з умовою 
. Такі елементи називаються оборотними.
Множина оборотних елементів кільця з одиницею складає групу - т.зв. мультиплікативну групу кільця. Мультиплікативна група кільця 
називається групою одиниць і позначається 
або 
.
Прикладом комутативного кільця з одиницею є множин цілих чисел. Група одиниць цього кільця складається з двох елементів: 
.
Поля.
