Примеры определения средних ошибок средних и относительных величин

 

mM = s √ n
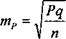
У 49 больных гипертиреозом исследован уровень пепсина n=49 М=1.0 г% s = 0,35 г% mм =?   mм = 0,35 = ± 0,05 г % √49	Исследовано 110 больных с абсцес­сом легкого, из них у 44 обнаруже­ны дистрофические изменения пародонта n=110   Р = 44*100 = 40%     лиц с дистрофиче­скими изменениями пародонта q= 100 - 40=60% лиц без дистрофи­ческих изменений пародонта mр=?   mр= √ 40*60 = ± 4,7%

 

 

Каждая средняя арифметическая или относительная величина, полу­ченная на выборочной совокупности, должна быть представлена со своей средней ошибкой. Это дает возможность рассчитать доверительные грани­цы средних и относительных величин, а также определить достоверность разности сравниваемых показателей (резултатов исследования).

6.2 Определение доверительных границ генеральной совокупности.

Определяя для средней арифметической (или относительной) величи­ны два крайних значения: минимально возможное и максимально возмож­ное, находят пределы, в которых может быть искомая величина генераль­ного параметра. Эти пределы называют доверительными границами.

Доверительные границы — это то максимальное и минимальное зна­чение, в пределах которого, при заданной степени вероятности безоши­бочного прогноза, может колебаться искомая средняя величина генераль­ного параметра.

Доверительные границы средней арифметической в генеральной со­вокупности определяют по формуле:

 

М ген = М выб ± tm_М

 

Доверительные границы относительной величины в генеральной со­вокупности определяют по следующей формуле:

Р ген = Р выб ± tm_Р

где Мген и Рген — значения средней и относительной величин, полу­ченных для генеральной совокупности; Мвы6 и Рвы6 — значения средней и относительной величин, полученных для выборочной совокупности; т_М и т_Р — ошибки репрезентативности выборочных величин; t — доверитель­ный критерий (критерий точности, который устанавливают при планиро­вании исследования; tm — доверительный интервал; tm=∆, где ∆ предель­ная ошибка показателя, полученного при выборочном исследовании.

Размеры предельной ошибки (∆) зависят от коэффициента t, который избирает сам исследователь, исходя из необходимости получить результат с определенной степенью точности.

Величина критерия t связана определенными отношениями с вероят­ностью безошибочного прогноза — р и численностью наблюдений в выбо­рочной совокупности.

Зависимость доверительного критерия t от степени вероятности безошибочного прогноза (при n>30)

 

Степень вероятности безошибочного прогноза в %	Доверительный критерий - t
95,0
99,0

 

Для большинства медико-биологических и социальных исследований достоверными считаются доверительные границы, установленные с веро­ятностью безошибочного прогноза р = 95% и более. Чтобы найти критерий t при числе наблюдений n<30, необходимо воспользоваться специальной таблицей, в которой слева показано число наблюдений без единицы (n-1), а сверху (р) — степень вероятности безошибочного прогноза.

 

Значение критерия t для трех степеней вероятности (по Н А. Плохинскому)

 

	Р		Р
n=n— 1	95%	99%	99,9%	n=n— 1	95%	99%	99,9%
	12,7	63,7	37,0		2,2	3,2	4,6
	4,3	9,9	31,6		2,2	3,1	4,4
	3,2	5,8	12,9		2,2	3,1	4,3
	2,8	4,6	8,6		2,2	3,0	4,1
	2,6	4,0	6,9	14—15	2Д	3,0	4,1
	2,4	3,7	6,0	16—17	2,1	2,9	4,0
	2,4	3,5	5,3	18—20	2Д	2,9	3,9
	2,3	3,4	5,0	21—2,4	2,1	2,8	3,8
	2,3	3,3	4,8	25—29	2,0	2,8	3,7

 

При определении доверительных границ сначала надо решить вопрос о том, с какой степенью вероятности безошибочного прогноза необходимо представить доверительные границы средней или относительной величи­ны. Избрав определенную степень вероятности, соответственно этому на­ходят величину доверительного критерия t при данном числе наблюдений. Таким образом, доверительный критерий t устанавливается заранее, при планировании исследования.

Любой параметр (средняя величина или относительная величина) мо­жет оцениваться с учетом доверительных границ, полученных при расчете.

Для ознакомления с методикой определения доверительных границ Мвыб и Рвы6 рекомендуется записать исходные данные и провести расчеты в определенной логической последовательности:

Пример 1. Определить доверительные границы среднего уровня пеп­сина у больных гипертиреозом с 95% вероятностью безошибочного про­гноза (р = 95%).

Условие задачи: n=49

Мвы6 = 1 г%

m_м = ±0,05 г%

р = 95% (следовательно при n = 49 t = 2).

Определяем доверительные границы средней величины в генеральной совокупности.

Формула Мген = Мвыб ± tm_M

Решение: Мген = 1 г% ± 2 х 0,05 г%

Мген не более 1 г%+0,1 г%= 1,1 г%,

Мген не менее 1 г%—0,1 г% =0,9 г%.

Вывод: Установлено с вероятностью безошибочного прогноза (р = 95%>, что средний уровень пепсина в генеральной совокупности у боль­ных с гипертиреозом не превышает 1,1 г% и не ниже 0,9 г%.

Пример 2. Определить доверительные границы показателя частоты дистрофии пародонта у больных с абсцессом легкого с вероятностью без­ошибочного прогноза р = 95%.

Условие задачи:

n=110

Рвы6 =40%

m_p = ±4,7%

р =95% (следовательно, при n=110 t=2).

Определяем доверительные границы относительного показателя в ге­неральной совокупности.

Формула: Рген = Рвыб ± tm_p,

Решение: Pген = 49% ±2 х 4,7%

Рген не более 40% + 9,4 = 49,4%

Рген не менее 40% -9,4 = 30,6%

Вывод: Установлено с 95% вероятностью безошибочного прогноза (р = 95%), что дистрофические изменения пародонта в генеральной совокуп­ности наблюдаются у больных с абсцессом легкого не чаще, чем в 49,4%, и не реже, чем в 30,6% случаев.

Как видно, доверительные границы зависят от размера доверительно­го интервала (tm=∆).

Анализ доверительных интервалов указывает, что при заданных сте­пенях вероятности (р) и n >30 t имеет неизменную величину и при этом доверительный интервал зависит от величины ошибки репрезентативности (m_M или m_Р).

С уменьшением величины ошибки суживаются доверительные грани­цы средних и относительных величин, полученных на выборочной сово­купности, т. е. уточняются результаты исследования, которые приближа­ются к соответствующим величинам генеральной совокупности.

Если ошибка большая, то получают для выборочной величины боль­шие доверительные границы, которые могут противоречить логической оценке искомой величины в генеральной совокупности.

Например, при определенном режиме питания и тренировок спорт­сменов средняя годовая прибавка массы тела у 80 спортсменов составила Мвы6=1 кг; m_M= ±0,8 кг. При степени вероятности р = 95,0% и t = 2 Мген = 1 кг ± 2 х 0,8 кг. Следовательно:

Мген не более + 2,6 кг,

Мген не менее - 0,6 кг.

Эти противоречивые данные означают, что при указанном режиме спортсмены могут дать большую среднюю прибавку массы тела (до +2,6 кг), но могут и убавить массу тела в среднем на 600 г. Таким образом, ос­тается по-прежнему невыясненным вопрос о степени влияния данного ре­жима спортсменов на массу их тела.

В подобном случае надо искать резервы сокращения размаха довери­тельных границ в размере величины ошибки репрезентативности. Прежде всего надо проанализировать уровень разнообразия признака по среднему квадратическому отклонению (s) с позиций однородности группы. Необ­ходимо также иметь в виду, что большое влияние на величину средней ошибки, а следовательно, и на доверительные границы оказывает числен­ность наблюдений.

Доверительные границы Мвыб и Рвыб зависят не только от средних ошибок этих величин (m_м или m_Р), но и от избранной исследователем сте­пени вероятности безошибочного прогноза (р). При большой степени ве­роятности размах доверительных границ увеличивается.