Тема 7: Корреляционно-регрессионный анализ.

Для расчета параметров уравнения регрессии (в основном используется линейное уравнение регрессии у = а₀ + а₁х) применятся, как уже упоминалось выше, метод наименьших квадратов, решая систему нормальных уравнений:

п а₀ + a₁Σх = Σу

а₀ Σt + a₁Σх² = Σх y

Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии. Значимость коэффициента регрессии осуществляется с помощью t-критерия Стьюдента:

,

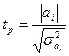где σ²_{а i} - дисперсия коэффициента регрессии.

Параметр модели признается статистически значимым, если 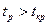(a; v=n-k-1), где a - уровень значимости, v=n-k-1 – число степеней свободы. Критическое значение коэффициента Стьюдента определяется по таблицам (приложение 4).

Величина σ²_{а i} может быть определена по выражению

,

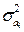
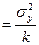где σ²_y - дисперсия результативного признака;

k – число факторных признаков в уравнении.

 

Оценка тесноты связи измеряется различными способами:

· при линейной зависимости - с помощью линейного коэффициента корреляции.

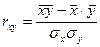или

.

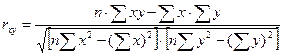Линейный коэффициент корреляции изменяется в пределах от –1 до 1: - 1 < r < 1.

· при криволинейной зависимости измеряется с помощью эмпирического корреляционного отношения.

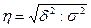
где 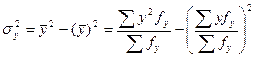дисперсия результативного признака;

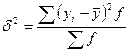- факторная дисперсия.

Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным.

a	b	a + b
c	d	c + d
a + c	b + d	a + b + c + d

Коэффициенты вычисляются по формулам:

ассоциации: ;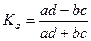

контингенции: .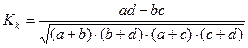

Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если К_а > 0.5 или К_k > 0.3.

Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова, которые вычисляются по следующим формулам:

,

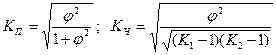где j² – показатель взаимной сопряженности;

j² – определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки минус 1:

,

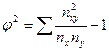где К₁ – число значений (групп) первого признака;

К₂ – число значений (групп) второго признака;

п_х , п_у - итоги по строкам и столбцам соответственно;

п_ху - значения признаков в ячейках таблицы.

Также коэффициенты Пирсона и Чупрова могут рассчитываться с использованием величины 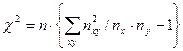, где n – число наблюдений.

; ,

 

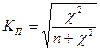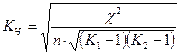Чем ближе величины К_П и К_Ч к 1, тем связь теснее.

 

Ранговые коэффициенты корреляции.

Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по формуле (для случая, когда нет связных рангов):

,

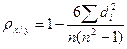где - квадраты разности рангов;

n – число наблюдений (число пар рангов).

При наличии связных рангов расчеты производятся по следующим формулам:

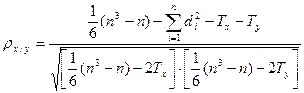
где 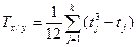, t_j – количество связных рангов.

Ранговый коэффициент корреляции Кендалла (τ) рассчитывается по формуле

,

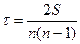где n – число наблюдений; S – сумма разностей между числом последовательностей и числом инверсий по второму признаку.

Расчет данного коэффициента выполняется в следующей последовательности:

1) значения х ранжируются в порядке возрастания или убывания;

2) значения у располагаются в порядке, соответствующем значениям х;

3) для каждого ранга у определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа, определяют величину Р как меру соответствия последовательностей рангов по х и у. Она учитывается со знаком «плюс»;

4) для каждого ранга у определяется число следующих за ним рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком «минус»;

5) определяется сумма баллов по всем членам ряда.

Если в изучаемой совокупности есть связные ранги, то расчеты необходимо проводить по следующей формуле:

,

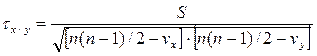где .

Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) W, который вычисляется по формуле:

,

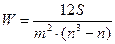где m – количество факторов; n – число наблюдений;

S – отклонение суммы квадратов рангов от средней квадратов рангов.

В случае наличия связных рангов коэффициент конкордации определяется по формуле:

,

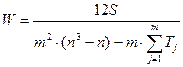где .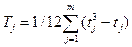

Приложение 1

Значения плотности φ(t) вероятности для нормированного нормального
закона распределения φ(t)=φ(-t)
t
0,0	0,3989	0,3989	0,3989	0,3988	0,3986	0,3984	0,3982	0,3980	0,3977	0,3973
0,1	0,3970	0,3965	0,3961	0,3956	0,3951	0,3945	0,3939	0,3932	0,3925	0,3918
0,2	0,3910	0,3902	0,3894	0,3885	0,3876	0,3867	0,3857	0,3847	0,3836	0,3825
0,3	0,3814	0,3802	0,3790	0,3778	0,3765	0,3752	0,3739	0,3725	0,3712	0,3697
0,4	0,3683	0,3668	0,3653	0,3637	0,3621	0,3605	0,3589	0,3572	0,3555	0,3538
0,5	0,3521	0,3503	0,3485	0,3467	0,3448	0,3429	0,3410	0,3391	0,3372	0,3352
0,6	0,3332	0,3312	0,3292	0,3271	0,3251	0,3230	0,3209	0,3187	0,3166	0,3144
0,7	0,3123	0,3101	0,3079	0,3056	0,3034	0,3011	0,2989	0,2966	0,2943	0,2920
0,8	0,2897	0,2874	0,2850	0,2827	0,2803	0,2780	0,2756	0,2732	0,2709	0,2685
0,9	0,2661	0,2637	0,2613	0,2589	0,2565	0,2541	0,2561	0,2492	0,2468	0,2444
1,0	0,2420	0,2396	0,2371	0,2347	0,2323	0,2299	0,2275	0,2251	0,2227	0,2203
1,1	0,2179	0,2155	0,2131	0,2107	0,2083	0,2059	0,2036	0,2012	0,1989	0,1965
1,2	0,1942	0,1919	0,1895	0,1872	0,1849	0,1826	0,1804	0,1781	0,1758	0,1736
1,3	0,1714	0,1691	0,1669	0,1647	0,1626	0,1604	0,1582	0,1571	0,1539	0,1518
1,4	0,1497	0,1476	0,1456	0,1435	0,1415	0,1394	0,1374	0,1354	0,1334	0,1315
1,5	0,1295	0,1276	0,1257	0,1238	0,1219	0,1200	0,1182	0,1163	0,1145	0,1127
1,6	0,1109	0,1092	0,1074	0,1057	0,1040	0,1023	0,1006	0,0989	0,0973	0,0957
1,7	0,0940	0,0925	0,0909	0,0893	0,0878	0,0863	0,0848	0,0833	0,0818	0,0804
1,8	0,0790	0,0775	0,0761	0,0748	0,0743	0,0721	0,0707	0,0694	0,0681	0,0669
1,9	0,0656	0,0644	0,0632	0,0620	0,0608	0,0596	0,0584	0,0573	0,0526	0,0551
2,0	0,0540	0,0529	0,0190	0,0508	0,0498	0,0488	0,0478	0,0468	0,0459	0,0449
2,1	0,0440	0,0431	0,0422	0,0413	0,0404	0,0396	0,0387	0,0790	0,0371	0,0363
2,2	0,0355	0,0347	0,0339	0,0332	0,0325	0,0317	0,0310	0,0303	0,0297	0,0290
2,3	0,0283	0,0277	0,0270	0,0264	0,0258	0,0252	0,0246	0,0241	0,0235	0,0229
2,4	0,0224	0,0219	0,0213	0,0203	0,0203	0,0198	0,0194	0,1890	0,0184	0,0180
2,5	0,0175	0,0171	0,0167	0,0163	0,0158	0,0154	0,0151	0,0147	0,0143	0,0139
2,6	0,0136	0,0132	0,0129	0,0126	0,0122	0,0119	0,0116	0,0113	0,0110	0,0107
2,7	0,0104	0,0101	0,0099	0,0096	0,0093	0,0091	0,0088	0,0086	0,0084	0,0081
2,8	0,0079	0,0077	0,0075	0,0073	0,0071	0,0069	0,0067	0,0065	0,0063	0,0061
2,9	0,0060	0,0058	0,0056	0,0055	0,0053	0,0051	0,0050	0,0048	0,0047	0,0046
3,0	0,0044	0,0043	0,0042	0,0040	0,0039	0,0038	0,0037	0,0036	0,0035	0,0034
4,0	0,0001	0,0001	0,0001	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000
Приложение 2     Значения χ2-критерия Пирсона при уровне значимости 0,10, 0,05, 0,01
к	0,1	0,05	0,01	к	0,1	0,05	0,01
	2,71	3,84	6,63		28,41	31,41	37,57
	4,61	5,99	9,21		29,62	32,67	38,93
	6,25	7,81	11,34		30,81	33,92	40,29
	7,78	9,49	13,28		32,01	34,17	41,64
	9,24	11,07	15,09		33,20	36,42	42,98
	10,64	12,59	16,81		34,38	37,65	44,31
	12,02	14,07	18,48		35,56	38,89	45,64
	13,36	15,51	20,09		36,74	40,11	46,96
	14,68	16,92	21,67		37,92	41,34	48,28
	15,99	18,31	23,21		39,09	42,56	49,59
	17,28	19,68	24,72		40,26	43,77	50,89
	18,55	21,03	26,22		51,80	55,76	63,69
	19,81	22,36	27,69		63,17	67,50	76,15
	21,06	23,68	29,14		74,40	79,08	88,38
	22,31	25,00	30,58		85,53	90,53	100,42
	23,54	26,30	32,00		96,58	101,88	112,33
	24,77	27,59	33,41		107,56	113,14	124,12
	25,99	28,87	34,81		118,50	124,34	135,81
	27,20	30,14	36,19

Значения функции Р(λ)
λ	Р	λ	Р
0,30		1,10	0,1777
0,35	0,9997	1,20	0,1122
0,40	0,9972	1,30	0,0681
0,45	0,9874	1,40	0,0397
0,50	0,9639	1,50	0,0222
0,55	0,9228	1,60	0,0120
0,60	0,8643	1,70	0,0062
0,65	0,7920	1,80	0,0032
0,70	0,7112	1,90	0,0015
0,75	0,6272	2,00	0,0007
0,80	0,5441	2,10	0,0003
0,85	0,4653	2,20	0,0001
0,90	0,3927	2,30	0,0001
0,95	0,3275	2,40	0,0000
1,00	0,2700	2,50	0,0000

Приложение 3

Приложение 4

Распределение Стьюдента

(t -распределение)

v	a=0,05	v	a=0,05
	12,706		2,101
	4,303		2,093
	3,182		2,066
	2,776		2,08
	2,571		2,074
	2,447		2,069
	2,365		2,064
	2,306		2,06
	2,262		2,056
	2,228		2,052
	2,201		2,048
	2,179		2,045
	2,16		2,042
	2,145		2,021
	2,131
	2,12		1,98
	2,11	бесконечность	1,96