при решении задач по данной теме примем некоторые обозначения.
N – объем генеральной совокупности (число входящих в нее единиц);
n – объем выборки (число обследованных единиц);
- генеральная средняя (среднее значение признака в генеральной совокупности);
– выборочная средняя;
p – генеральная доля (доля единиц, обладающих данным значением признака, в общем числе единиц генеральной совокупности), например, доля числа бракованных единиц в общем количестве единиц в данной партии изделий;
w – выборочная доля;
s2 – генеральная дисперсия (дисперсия признака в генеральной совокупности);
S2 – выборочная дисперсия того же признака;
s - среднее квадратическое отклонение в генеральной совокупности;
S – среднее квадратическое отклонение в выборке.
Между характеристиками выборочной совокупности и искомыми характеристиками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой выборки.
Задачи, решаемые в этой теме, обусловлены практическими вопросами, требующими своего решения при организации выборочного наблюдения и анализе его результатов. Такими вопросами являются определение способа отбора и процедуры выборки; вычисление ошибок выборки и построение доверительных интервалов выборочных характеристик, а также расчетов необходимого объема выборки.
Различают среднюю и предельную ошибки выборки. Эти два вида ошибок связаны следующим соотношением:
где Δ – предельная ошибка выборки;
μ – средняя ошибка выборки;
t – коэффициент доверия, определяемый в зависимости от уровня вероятности.
Чаще всего используют следующие сочетания:
| t | P |
| 1,0 | 0,683 |
| 1,5 | 0,866 |
| 1,96 | 0,950 |
| 2,0 | 0,954 |
| 2,5 | 0,988 |
| 2,58 | 0,990 |
| 3,0 | 0,997 |
| 3,5 | 0,999 |
Предельные ошибки выборки (
) определяются в зависимости от метода отбора по формулам:
| Метод отбора | Формулы объема выборки | |
| Для средней | Для доли | |
| Повторный | 
| 
|
| Бесповторный | 
| 
|
После вычисления предельных ошибок выборки находят доверительные интервалы для генеральных показателей. Для `Х это (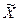
± Δх). Для Р это (W ± Δw), т.е.
Доля признака (W=m/n) – доля единиц, обладающих определенным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
Дисперсия доли находится следующим образом:
σw2 = W*(1 - W)
Формулы, приведенные выше, используются при определении ошибок выборки, осуществляемой собственно случайным или механическим методами. В случае с типической выборкой показателем вариации является средняя из внутригруппировочных дисперсий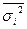 
; при серийной выборке - межгрупповая (межсерийная) дисперсия δ2 и т.д. Кроме того, в последнем случае вместо объема выборочной совокупности n используется показатель числа серий r.
· Для типической выборки предельная ошибка вычисляет следующим образом:
- при отборе, пропорциональном объему типических групп:
- повторный отбор,
- бесповторный отбор.
- при отборе, пропорциональном вариации признака (непропорциональном объему типических групп):
- повторный отбор,
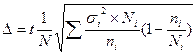- бесповторный отбор,
где Ni и ni – объемы i-ой типической группы и выборки из нее соответственно,
i2 – групповые дисперсии.
· При серийной выборке предельная ошибка определяется:
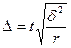- повторный отбор,
- бесповторный отбор,
где R и r – число серий в генеральной и выборочной совокупности соответственно,
δ2 – межгрупповая (межсерийная) дисперсия, которая находится по следующей формуле:
где 
- серийные средние,
- общая средняя.
Разрабатывая программу выборочного наблюдения, задают величину допустимой ошибки выборки и доверительную вероятность. Неизвестным остается тот минимальный объем выборки, который должен обеспечить требуемую точность. Формулы для определения численности выборки (n) зависят от метода отбора. Они различны для расчета средней и доли и следуют из формул предельных ошибок выборки:
| Метод отбора | Формулы объема выборки | |
| Для средней | Для доли | |
| Повторный | 
| 
|
| Бесповторный |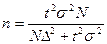 
| 
|
