Для характеристики интенсивности измерения во времени такими показателями будут:
1) абсолютный прирост; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста.
В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.
Расчет показателей динамики представлен в следующей таблице: Таблица 10.
| Показатель | Базисный | Цепной |
| Абсолютный прирост (Di баз; Di цеп)* | 
| 
|
| Коэффициент роста (Кр)** | 
| 
|
| Темп роста (Тр) |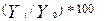 
| 
|
| Коэффициент прироста (Кпр) | Кр- 1;
 ;
| Кр- 1;
 ;
|
| Темп прироста (Тпр) |  ;
|  ;
|
| Абсолютное значение одного процента прироста (А) |
|  ;
 ;
|
* - 
** - 
.
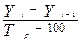
Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Средний уровень ряда расчитывается:
· интервальный ряд:
с равными периодами времени
где n – общая длина временного ряда или общее число равных временных отрезков.
с неравными периодами времени
· моментный ряд
с равными периодами
.
с неравными интервалами
где ti – число периодов, в течении которых уровень ряда не изменялся.
- среднегодовой абсолютный прирост
- среднегодовой темп роста,
где 
- средний коэффициент роста, рассчитанный как
.
Здесь Кцеп – цепные коэффициенты роста; Кбаз – базисный коэффициент роста;
т=п - 1 – число коэффициентов роста; п – количество периодов.
- среднегодовой темп прироста.
При выполнении смыкания рядов (при приведении рядов к сопоставимому виду) можно применить два способа:
1. определяют коэффициент смыкания Ксмык по тому периоду, в котором произошли изменения. Данный коэффициент равен отношению уровня ряда после изменения к уровню ряда до изменения. Чтобы получить недостающие уровни после изменения, необходимо уровни до изменения умножить на коэффициент смыкания.
2. уровни года (периода), в котором произошли изменения, как до так и после изменения принимаются за 100%, а остальные пересчитываются в процентах по отношению к этим уровням соответственно. В результате получается сомкнутый ряд.
Выявление тренда может проводится несколькими способами:
1. Укрупнение интервалов.
2. Скользящая средняя. Суть метода в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средней ведется способом скольжения, т.е. постепенным исключением из примятого периода первого уровня и включением следующего.
Для 3–членной Ŷi = 
;
При нахождении скользящей средней по четному числу членов средняя относится к середине между двумя датами. Затем проводится центрирование, т.е. нахождение средней из средних для отнесения полученного уровня к определенной дате.
3. Аналитическое выравнивание. При этом уровни ряда выражаются в виде функции времени: 
Чаще всего при выравнивании используются следующие зависимости:
Линейная f(t) = a0 + a1t;
Параболическая f(t) = a0 + a1t + a2t2;
Экспоненциальнaя f(t) = exp (a0 + a1t).
Оценка параметров (а0, а1, а2, …) осуществляется чаще методом наименьших квадратов (МНК). Так, при выравнивании ряда по прямой для нахождения параметров прямой решается система нормальных уравнений вида
п а0 + a1Σt = Σу
а0 Σt + a1Σt2 = Σt y
Для упрощения счета при выравнивании динамических рядов условное обозначение временных точек (t) можно вести так, чтобы Σt=0. В этом случае системы нормальных уравнений значительно упрощаются.
Так, при выравнивании по прямой система будет иметь вид:
п а0 = Σу
а1 Σt2 = Σty
При выравнивании по параболе второго порядка (если Σt=0) система имеет следующий вид:
п а0 + a2Σt2 = Σу
а1 Σt2 = Σty
а0 Σt2 + a2Σt4 = Σt2 y
При изучении сезонных колебаний используются индексы сезонности Is:
где уi – уровни ряда;
- средний уровень ряда.
Однако данные одного года могут быть случайными и не отражать общей закономерности колебаний. Поэтому на практике для выявления закономерности пользуются помесячными данными за ряд лет. Тогда для каждого месяца рассчитывается средний уровень, и формула принимает следующий вид:
,
где 
- средняя для каждого месяца за 3 года;
- общий средний месячный уровень за 3 года.
