Индивидуальный индекс цены рассчитывается по формуле: 
, где
р1 – цена товара в текущем периоде;
р0 – цена товара в базисном периоде.
Индивидуальный индекс физического объема реализации: 
, где
q1 – количество товара, реализованное в текущем периоде,
q0 – количество товара, реализованное в базисном периоде.
Индивидуальный индекс товарооборота: 
.
Сводный индекс товарооборота:
.
Сводный индекс цен по методу Пааше 
,
В данном случае фиксируется количество проданного товара на текущем уровне.
- с водный индекс цен по методу Ласпейреса, здесь фиксируется количество проданного товара на базисном уровне. В случае, когда не указано, по какому методу рассчитать сводный индекс цен, его рассчитывают по методу Пааше.
Сводный индекс физического объема реализации.
.
Разность числителя и знаменателя сводного индекса цен будет отражать величину экономии (если знак "-") или перерасхода ("+") покупателей от изменения цен: Е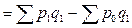 
Между данными индексами существует следующая взаимосвязь:
.
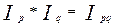Следующая группа индексов включает индексы затрат на производство, себестоимости и физического объема продукции, которые представлены ниже соответственно:
где z1 и z0 - себестоимость продукции в текущем и базисном периоде соответственно;
q1 и q0– количество продукции, произведенное в текущем и базисном периоде.
Разность числителя и знаменателя сводного индекса себестоимости показывает сумму экономии предприятия от снижения себестоимости:
Е = Σz1q1 - Σ z0q1
Между данными индексами существует следующая взаимосвязь:
В зависимости от условий применения средний арифметический или средний гармонический индексы, тождественные агрегатной форме индекса. Индексы качественных показателей (цен, себестоимости и др.) определяются по средней гармонической из индивидуальных индексов. Так, агрегатный индекс цен преобразуется в среднегармонический индекс цен:
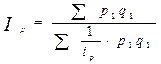
Индексы объемных, количественных показателей (физического объема реализации, продукции и др.) определяются по средней арифметической из индивидуальных индексов. Так, агрегатный индекс количествва реализованных товаров преобразуется в среднеарифметический индекс:
Все рассмотренные выше индексы рассчитывались по нескольким товарам, реализуемым в одном месте, или видам продукции, производимым на одном предприятии. Рассмотрим теперь случай, когда один товар реализуется в нескольких местах или вид продукции производится на ряде предприятий.
Если реализуется только один вид продукции, вполне правомерно рассчитывать его среднюю цену в каждом периоде. Индекс переменного состава представляет собой отношение двух полученных средних значений:
.
Следующий индекс характеризует не только изменение индивидуальных цен в местах продажи, но и изменение структуры реализации по предприятиям розничной или оптовой торговли, рынкам, городам и регионам. Для оценки воздействия этого фактора рассчитывается индекс структурных сдвигов:
.
Последним в данной системе является рассмотренный выше индекс цен фиксированного состава, который не учитывает изменение структуры:
.
Между данными индексами существует следующая взаимосвязь: 
.
Территориальные индексы. Территориальные индексы служат для сравнения показателей в пространстве, т.е. по предприятиям, округам, городам, районам и пр. Существует 2 способа расчета таких индексов.
1. данный способ заключается в том, что в качестве весов принимаются объемы проданных товаров по двум регионам, вместе взятым:
Q = qa + qb.
Тогда индекс цен в этом случае рассчитывается по следующей формуле:
2. здесь учитывается соотношение весов сравниваемых территорий. При этом способе первый шаг заключается в расчете средней цены каждого товара по двум территориям, вместе взятым:
.
После этого непосредственного рассчитывается территориальный индекс:
.
Задача 75.
Имеются следующие данные о реализации товаров:
| товар | 1 полугодие | 2 полугодие | ||
| p0 | q0 | p1 | q1 | |
| А | ||||
| Б | ||||
| В | ||||
| Г |
Определить: сводные индексы цен Пааше и Ласпейреса, физического объема реализации, товарооборота.
