Средняя ошибка выборки при случайной повторной выборке (формула П.Л.Чебышева) (m):
.
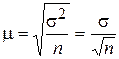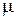уменьшается при уменьшении колеблемости признака, а также при увеличении объема выборочной совокупности. Следовательно, при уменьшении колеблемости признака можно уменьшить объем выборочной совокупности.
Средняя ошибка выборки при определении доли признака:
,
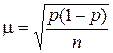где 
– доля признака в генеральной совокупности;
– число единиц в выборочной совокупности;
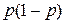– дисперсия доли признака.
Для бесповторного отбора:
· для определения ошибки выборочной средней:
,
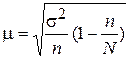где 
– число единиц в генеральной совокупности.
· для определения ошибки выборочной доли
.
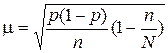Предельной ошибкой выборки принято называть максимально возможное расхождение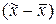 
, т.е. максимум ошибки при заданной вероятности ее появления.
Предельная ошибка при повторном отборе:
· для средней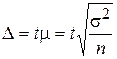 
,
где t – заданный коэффициент доверия (критерий кратности ошибки выборки).
t = 1 Р = 0,683
t = 2 Р = 0,954
t = 3 Р = 0,997
· для доли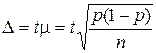 
.
При бесповторном отборе предельные ошибки выборки должны определяться:
· для средней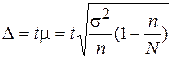 
;
· для доли 
.
Предельная ошибка выборки позволяет определять предельные значения характеристик генеральной совокупности при заданной вероятности и их доверительные интервалы:
.
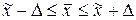
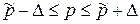Это значит, что с заданной вероятностью можно утверждать, что значение генеральной средней можно ожидать в пределах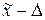 
до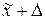 
.
Рассчитывается также относительная ошибка выборки:
.
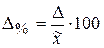Одной из важных задач при проведении выборочного наблюдения является установление необходимой численности выборочной совокупности, т.е. такой ее численности, которая обеспечивала бы получение данных, достаточно полно отражающих изучаемые свойства генеральной совокупности.
Необходимая численность выборки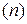 
устанавливается в зависимости от размеров предельной ошибки (
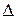), от величины коэффициента доверия (t) и от размеров величины дисперсии (
).
При повторном отборе:
· для средней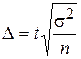 
обе стороны возводим в квадрат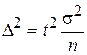 
, следовательно:
;
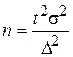· для доли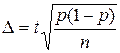 
обе стороны возводим в квадрат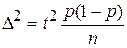 
,
тогда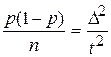 
, 
.
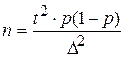При бесповторном отборе:
· для средней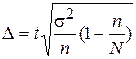 
,
следовательно: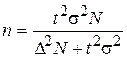 
;
· для доли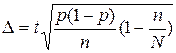 
,
следовательно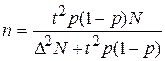 
.
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основании выборки. При этом на генеральную совокупность распространяют не только средние и относительные величины, но производят и расчет объемных показателей по всей генеральной совокупности на основании полученных в результате выборочного наблюдения данных. Применяют следующие способы распространения выборочных данных на всю генеральную совокупность:
1. Способ прямого пересчета основан на том, что средние величины или соотношения отдельных частей, полученные в результате выборочного наблюдения, умножают на число единиц генеральной совокупности.
2. Способ коэффициентов основан на том, что, сопоставляя данные сплошного наблюдения с данными выборочного обследования, устанавливают коэффициент, который служит для внесения поправок в данные сплошного наблюдения.
Контрольные вопросы к теме №7
1. Сущность выборочного отбора.
2. Назовите основные виды выборочного наблюдения.
3. Понятие «репрезентативности» выборочного наблюдения.
4. Как определить среднюю ошибку выборки для бесповторного отбора?
5. Как определить доверительный интервал для генеральной средней?
6. Назовите основные способы распространения выборочных данных на генеральную совокупность.
