Общий индекс физического объема продукции

где – индексируемая величина;

– вес;

– цены сопоставимые (базисные).

К индексам качественных показателей относятся индексы цен, индексы себестоимости продукции, индексы средней заработной платы, индексы производительности труда, индексы удельных расходов материалов. Эти индексы характеризуют показатели, которые носят расчетный характер. Они измеряют интенсивность, эффективность явления и являются либо средними, либо относительными величинами.

Рассмотрим расчет индивидуального и общего индекса качественных показателей на примере индекса цен.

Индивидуальный индекс цен характеризует изменение цены по каждому виду продукции:

где и – соответственно цена отчетного и базисного периода.

Перед общим (агрегатным) индексом качественного показателя ставится задача измерить не только относительное изменение уровня, но и абсолютную величину того экономического эффекта, который получен в текущем периоде в результате этого изменения. В данном случае сумму экономии покупателей за счет снижения цен, или сумму их дополнительных расходов, если цены повысились.

Для получения общего индекса цен нужно построить его так, чтобы отразилось влияние только фактора изменения цен, и было бы исключено влияние изменения количества проданных товаров. Это возможно в том случае, если для обоих сравниваемых периодов количество проданных товаров будет взято одинаковое. Количество проданных товаров следует брать в текущем периоде, так как только на приобретении этого количества потребитель может экономить в результате снижения цен или перерасходовать в результате их повышения.

Общий индекс цен:

– индекс цен Пааше,

где – индексируемая величина; – веса.

В числителе индекса дана суммарная стоимость проданных в текущем периоде товаров по ценам текущего периода, а в знаменателе – стоимость того же количества товаров, но рассчитанная по ценам базисного периода.

Экономия (перерасход) от изменения цен: .

В статистике используются и другие формы представления общих индексов цен – Ласпейреса и Фишера:

– индекс цен Ласпейреса,

– индекс цен Фишера.

Если при исчислении индексов сравниваемых периодов три и более, то возникает вопрос о выборе базы сравнения. В зависимости от базы сравнения различают цепные и базисные индексы.

Цепные индексы получают путем сопоставления индексируемого показателя любого периода с показателем предшествующего ему периода. Базисные индексы вычисляются путем сравнения индексируемого показателя каждого периода с соответствующим показателем периода, принятого за базу сравнения.

Цепные и базисные индексы могут быть как индивидуальные, так и общие.

Между цепными и базисными индексами существует определенная взаимосвязь, которая для индивидуальных индексов проявляется всегда, а для агрегатных индексов – лишь при определенных условиях.

Базисные индивидуальные индексы:

; ; .

Цепной индивидуальный индекс:

; ; .

Последовательное перемножение цепных индивидуальных индексов дает возможность получить базисный индекс:

Базисный агрегатный индекс физического объема продукции:

; .

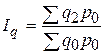Цепной агрегатный индекс физического объема продукции:

; .

Последовательно перемножение цепных агрегатных индексов физического объема продукции дает возможность получить базисный индекс:

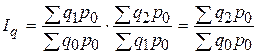Агрегатные индексы качественных показателей всегда являются индексами с переменными весами, так как при их исчислении всегда используются веса отчетного периода. Поэтому цепной метод исчисления базисных индексов для них не приемлем.

Таблица 24

Цепные и базисные индексы

Индексы	Базисные	Цепные
физического объема продукции		; ; ;	; ; ;
	; ; ;	; ; ;
цен		; ; ;	; ; ;
	; ;	; ;
стоимости		; ;	; ;
	; ;	; ;

Агрегатный способ исчисления общих индексов является основным, но не единственным в статистике. В ряде случаев из-за отсутствия некоторых данных нельзя произвести расчет по формуле агрегатного индекса. Это может иметь место в том случае, если нет данных об абсолютном значении индексируемой величины, т.е. величины показателя, характеризующего ту сторону явления, изменение которой изучается (например, при исчислении индекса физического объема продукции нет данных об объеме производства в целом). В этом случае применяются средние индексы.

Мы знаем, что индивидуальный индекс физического объема выражается , следовательно, . Если в формуле агрегатного индекса заменить на выражение , то получим формулу среднего арифметического индекса физического объема:

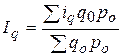Пример.

Таблица 25

Наименование товара	Изменение объема продаж в отчетном периоде по сравнению с базисным, %	Товарооборот в базисном периоде, млн.руб.
Картофель	+25
Капуста	+75
Молоко	без изменения

Определить общий индекс физического объема продукции.

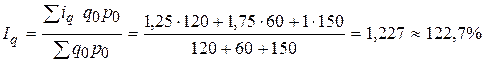(объем выпуска увеличился на 22,7%).

В тех случаях, когда нет данных о количестве проданных товаров, нельзя исчислить агрегатный индекс цен, но если известны индивидуальные индексы цен, а также имеются данные о продажах в текущем периоде в ценах текущего периода, таким образом, можно исчислить средний гармонический индекс цен.

Из формулы индивидуального индекса цен 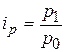, определим . Если в агрегатном индексе цен заменить в знаменателе на , то получим формулу среднего гармонического индекса цен: .

Пример.

Таблица 26

Наименование товара	Изменение цены в отчетном периоде по сравнению с базисным, %	Товарооборот в текущем периоде, млн.руб.
Картофель	-25	112,5
Капуста	-17	87,5
Молоко	+17	175,0

Определить общий индекс цены:

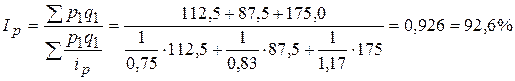
(цены снижены на 7,4%).

Изменение структуры изучаемой совокупности оказывает влияние на динамику экономических явлений. Рассмотрим это положение на примере изменения цен на всех рынках на какой-то один товар. Изменение цен может быть результатом двух факторов: изменения уровня цен на отдельных рынках и изменения в соотношении количества данного товара, реализованного на отдельных рынках с разным уровнем цен на этот товар.

Во-первых, определим результат совместного действия обоих факторов. В этом случае индекс цен на какой-то товар определяется, как отношение средней цены текущего периода к средней цене базисного периода. Для определения средних цен текущего и базисного периода в качестве весов принимается количество реализованного товара в соответствующих периодах:

Отношение двух взвешенных средних с изменяющимися (переменными) весами, показывающее изменение индексируемой величины, принято называть индексом переменного состава.

Чтобы определить изменение уровня цен в чистом виде, надо устранить влияние изменения структуры продаж:

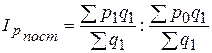Отношение средних взвешенных с одними и теми же весами называется индексом постоянного (фиксированного) состава.

Для определения влияния изменения соотношения количества проданного товара на разных рынках необходимо устранить влияние изменения цен на отдельных рынках, т.е. зафиксировать их на базисном уровне. Для этих целей рассчитывается индекс структурных сдвигов:

Все экономические явления находятся во взаимосвязи друг с другом. Так, стоимость выработанной продукции зависит от количества выработанной продукции и цены за единицу продукции. Также связаны и индексы, характеризующие изменения этого явления:

; .

Перемножим данные индексы:

Следовательно, .

На основании двух индексов при единстве методологии их построения может быть исчислен третий. Так, если объем производства возрос на 10%, а цена снизилась на 5%, то изменение стоимости составит: 1,1 · 0,95 = 1,157 или 115,7%.

Индексный метод широко используется при анализе роли отдельных факторов в динамике какого-либо сложного явления. При этом индексный метод позволяет определить размер абсолютного изменения сложного явления за счет каждого фактора в отдельности.

Сложным явлением следует считать такой показатель, который может быть представлен как произведение двух и более показателей. Предположим, что сложное явление А представляет собой произведение двух показателей: a и b, т.е. А=a · b, или , где – средняя заработная плата, – среднесписочная численность работающих. Изменение сложного явления может быть представлено индексом:

или .

Абсолютное изменение явления под влиянием всех факторов представляет разность между числителем и знаменателем:

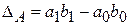или .

Задача заключается в том, чтобы выявить влияние каждого фактора в отдельности. Для этого индекс сложного явления разлагают на частные индексы, характеризующие роль каждого фактора.

Сущность метода обособленного изучения факторов заключается в том, что при выявлении роли каждого фактора сложное явление в отчетном периоде берется в том виде, какой бы оно имело, если бы изменился один данный фактор, а прочие бы остались неизменными (на уровне базисного периода).

Роль каждого фактора определим:

или ,

абсолютное отклонение:

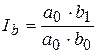или

или ,

абсолютное отклонение:

или .

Общее изменение явления А может быть представлено, как произведение частных индексов:

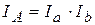, или .

В результате суммирования абсолютных отклонений получается неразложимый остаток, который можно рассматривать как результат совместного действия всех факторов.

При последовательно-цепном методе используется система взаимосвязанных частных индексов. При этом методе, выявляя влияние качественного фактора, объемный фактор при построении индекса сохраняют на уровне отчетного периода; при построении индекса объемного фактора качественный фактор берется на уровне базисного периода.

Если a – качественный фактор, b – объемный фактор:

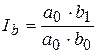; абсолютное отклонение ;

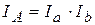В данном случае .

Контрольные вопросы к теме №9

1. Что характеризует индивидуальный индекс?

2. Формула для расчета общего индекса стоимости.

3. Когда используются средние индексы?

4. Как определить среднегармонический индекс цены?

5. Цепные и базисные индексы.

6. Индексы переменного, постоянного состава и структурных сдвигов.

7. Индексный метод выявления влияния отдельных факторов на экономическое явление.