| Годы | До изменения границ области (в старых границах) | После изменения границ области (в новых границах) | 2000 г. = 100% | Сомкнутый ряд динамики (2000 г. = 100%) | Абсолютные уровни в новых границах | |
| в старых границах | в новых границах | |||||
| – | – | |||||
| – | – | |||||
| – | – | |||||
| – | – |
Одна из важнейших задач анализа динамики – выявление и количественная характеристика основной тенденции развития явления. Под тенденцией понимается общее направление к росту, снижению или стабилизации уровня явления с течением времени. Однако рост и снижение уровня могут происходить либо равномерно, либо ускоренно, либо замедленно.
1 – равномерный рост
2 – замедленный рост
3 – ускоренный рост
4 – равномерное снижение
5 – замедленное снижение
6 – ускоренное снижение
Под равномерным ростом или снижением здесь понимается рост (снижение) с постоянной абсолютной скоростью, когда цепные абсолютные приросты одинаковы. При ускоренном росте цепные приросты систематические увеличиваются по абсолютной величине, а при замедленном росте или снижении – уменьшаются. Однако практически уровни ряда динамики очень редко растут или снижаются строго равномерно. Поэтому при анализе динамики идет речь не просто о тенденции развития, а об основной тенденции, достаточно стабильной и устойчивой на протяжении данного этапа развития.
Основной тенденцией (трендом) называется достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайных колебаний. Основную тенденцию можно представить либо аналитически – в виде уравнения (модели) тренда, либо графически. В тех случаях, когда уровень ряда динамики то повышается, то понижается или же изменяется в одном направлении, но очень неравномерно, целесообразно сравнивать и использовать при расчете показателей динамики не годовые, а более типичные среднегодовые уровни, изменение которых лучше отражает основную тенденцию развития. Возможны и другие способы и приемы выявления и характеристики основной тенденции.
Способ укрупнения интервалов. Этот способ заключается в переходе от интервалов менее продолжительных к более продолжительным (переход от суток – к неделям, от месяцев – к кварталам или годам, от годовых интервалов – к многолетним). Если уровни ряда динамики колеблются с более или менее определенной периодичностью, волнообразно, то укрупненный интервал целесообразно взять равным периоду колебаний (длине волны цикла). Если же такая периодичность отсутствует, то укрупнение производят постепенно от малых интервалов ко все более крупным, пока общее направление тренда не станет явным.
Метод скользящей средней. Он заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней начиная со второго и т.д. Полученная средняя относится к середине укрупненного интервала.
; 
; 
.
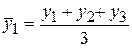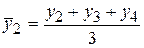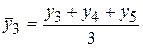Скользящая средняя имеет недостатки:
1) невозможность получения уровней для концов сглаживаемого ряда;
2) произвольность выбора интервала сглаживания.
Выравнивание ряда по прямой предусматривает решение следующего уравнения: 
, где t – время (порядковый номер интервала или момент времени).
Расчет параметров значительно упрощается, если 
.
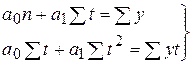
, следовательно 
– средний уровень ряда;
, следовательно 
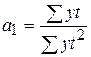– средний абсолютный прирост.
При нечетном числе уровней ряда, уровень, находящийся в середине ряда, принимается равным нулю. Даты времени, стоящие выше этого времени, будут обозначаться натуральными числами со знаком «–»: –1; –2; –3; ниже со знаком «+»: +1; +2; +3. Сумма t должна быть равна нулю.
Если число уровней ряда четное, то значения t будут следующими:
| -3 | -2 | -1 |
После нахождения параметров уравнения составляется уравнение прямой ряда динамики. По нему рассчитываются уровни выровненного ряда динамики. Правильность расчета уровней выровненного ряда динамики может быть проверена следующим образом: сумма значений эмпирического ряда должна совпадать с суммой вычисленных значений уровней выровненного ряда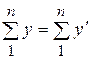 
. Затем графически изображают уровни эмпирического ряда и выровненного.
Прогнозирование – это определение ориентировочных размеров явлений в будущем. Продление тенденции в будущее, наблюдавшейся в прошлом, называется экстраполяцией. Возможность экстраполяции обеспечивается двумя обстоятельствами:
1) общие условия, определяющие тенденцию развития в прошлом, не претерпевают существенных изменений в будущем;
2) тенденция развития явления характеризуется тем или иным аналитическим уравнением.
Интерполяция – приближенный расчет уровней, лежащих внутри ряда динамики, но почему-то неизвестных. При изменении уровней ряда в арифметической прогрессии неизвестный уровень ряда определится:
,
где 
, 
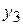– рядом лежащие уровни.
Если уровни изменяются в геометрической прогрессии, то:
.
Сезонные колебания – это сравнительно устойчивые внутригодичные колебания явления. Они вызываются рядом объективных причин (природно-климатическими) и ведут к ухудшению показателей работы предприятий. Анализ сезонных колебаний необходим для улучшения оперативного планирования и разработки мероприятий для уменьшения их отрицательных воздействий.
При изучении сезонной неравномерности перед статистикой ставятся две задачи:
· выявить сезонную неравномерность;
· определить ее размеры (рассчитать сезонную волну).
Наличие сезонной неравномерности выявляется при помощи графического метода. Для этого используются линейные диаграммы, на которые наносят данные о среднесуточном производстве товара по месяцам, но не менее, чем за 3 года. На графике будут построены несколько ломанных линий. Среднесуточное производство из года в год может увеличиваться, однако если максимальный и минимальный объемы для всех трех лет приходятся на одинаковые месяцы, то можно говорить о наличии сезонной неравномерности.
Для измерения сезонных колебаний предложены следующие методы:
· метод абсолютных разностей;
· метод относительных разностей;
· построение индексов сезонности.
При использовании метода абсолютных разностей вначале определяют средний уровень явления за каждый месяц по 3-х летним данным, затем определяют среднюю за весь рассматриваемый период.
Далее определяется абсолютное отклонение средних за каждый месяц от общей средней.
Метод относительных разностей является развитием метода абсолютных разностей. Для нахождения относительных разностей абсолютные отклонения делят на общую среднюю и выражают в процентах.
Глубину сезонных колебаний измеряют индексами сезонности (I сез):
,
где 
– средняя из фактических средних уровней одноименных месяцев;
– общая средняя за исследуемый период.
Индекс сезонности показывает, на сколько среднемесячное потребление каждого месяца отличается от общего среднего за весь период.
Контрольные вопросы к теме №8
1. Что называется динамикой?
2. Виды динамических рядов.
3. Как определить темп роста?
4. Как определить средний уровень моментного ряда с неравными интервалами?
5. Как определить средний коэффициент роста?
6. Методы выявления и характеристики основной тенденции.
7. Как найти индекс сезонности?
