Статистический анализ многофакторного опыта должен количественно установить существенность влияния каждого из изучаемых факторов и их взаимодействий на результативный признак.
Основной особенностью анализа данных многофакторного опыта является разложение общего варьирования вариантов СV на компоненты действия изучаемых факторов и их взаимодействия. Например, если мы изучаем в многофакторном опыте одновременно влияние удобрений и орошения на урожайность пшеницы, то мы должны общее варьирование вариантов, вызванное применением этих агротехнических приёмов разложить на варьирование урожайностей, происходящее под действием орошения, варьирование урожайностей, обусловленное действием удобрений и варьирование урожайностей, обусловленное взаимодействием (или комплексным влиянием) этих двух факторов. Эффект взаимодействия (например, орошения и удобрений) составляет ту часть общего варьирования, которая вызвана различным действием одного фактора при разных градациях другого. Специфическое действие сочетаний в многофакторном эксперименте выявляется тогда, когда при одной градации одного изучаемого фактора (например, без орошения в засушливых условиях) другой (удобрения) действует слабо или угнетающе на изучаемый показатель (урожайность пшеницы), а при другой градации (норма полива 300 т/га) он проявляется значительно сильнее и стимулирует развитие результативного признака (урожайность).
В полевом эксперименте часто эффект от совместного применения изучаемых факторов больше (синергизм) или меньше (антагонизм) суммы эффектов от раздельного применения каждого из них. Следовательно, существует взаимодействие факторов: в первом случае положительное, а во втором - отрицательное. Когда факторы не взаимодействуют, прибавка от совместного применения их равна сумме прибавок от раздельного воздействия (аддитивизм).
Статистическую обработку данных проводят в следующей последовательности:
1) исходные данные заносят в таблицу урожаев, определяют суммы и средние;
2) вычисляют суммы квадратов для общего варьирования 
, варьирования повторений 
, вариантов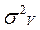 
и остатка 
, те.е обрабатывают данные так же, как и результаты однофакторного опыта;
3) общее варьирование разлагают на компоненты – главные эффекты изучаемых факторов и их взаимодействия;
4) составляют таблицу дисперсионного анализа и проверяют нулевую гипотезу о существенности действия и взаимодействия факторов по F -критерию.
Таким образом, многофакторный дисперсионный комплекс – это совокупность исходных наблюдений (дат), позволяющих статистически оценить действие и взаимодействие нескольких изучаемых факторов на изменчивость результативного признака.
Пример. Проведём статистическую обработку данных двухфакторного экологического опыта по изучению накопления свинца в зерне яровой пшеницы в зависимости от удалённости посевов от города Омска, км (фактор А) и от автомагистрали, м (фактор В).
Порядок вычислений при дисперсионном двухфакторном анализе во многом очень схож с обработкой данных однофакторного опыта этим методом:
1. После перенесения из журнала данных по полученному качеству зерна (или других наблюдений) в таблицу 25 подсчитываем суммы урожаев всех повторений для каждого варианта 
и суммы урожаев всех вариантов для каждого повторения 
при этом сумма всех сложенных повариантных данных должна быть равна сумме всех сложенных наблюдений по повторениям, то есть:
= 
.
В приведенном примере сумма всех поделяночных значений содержания свинца в зерне яровой пшеницы составила 546,2.
2. Все поделяночные наблюдения возводим в квадрат и записываем.
3. Определяем суммы квадратов наблюдений по опыту, а также суммы квадратов сложенных наблюдений по вариантам и повторениям. Вычисляют таким образом:
= 1190,3+912,0+1049,8+1232,0+88,4+……+941,0+32,5 = 12294,1
= 132,22 + 42,02 + +……+ 33,42 + 23,82 = 48903
= 140,02 + 141,42 + 132,62 + 132,22 = 74654
Таблица 14
| Фактор | Содержание Pb в почве по повторениям, мг/кг сухой массы |
| Среднее содержание свинца в зерне,
| Квадрат содержания свинца в зерне по повторениям (х2) | |||||||
| Удалённость от города (фактор А) | Удалённость от автомагистрали (фактор В) | I | II | III | IV | I | II | III | IV | ||
| 1 км | 10 м | 34,5 | 30,2 | 32,4 | 35,1 | 132,2 | 33,1 | 1190,3 | 912,0 | 1049,8 | 1232,0 |
| 110 м | 9,4 | 12,5 | 8,6 | 11,5 | 42,0 | 10,5 | 88,4 | 156,3 | 74,0 | 132,3 | |
| 210 м | 6,0 | 8,4 | 7,0 | 7,2 | 28,6 | 7,2 | 36,0 | 70,6 | 49,0 | 51,8 | |
| 11 км | 10 м | 30,3 | 30,5 | 28,4 | 26,5 | 115,7 | 28,9 | 918,1 | 930,3 | 806,6 | 702,3 |
| 110 м | 11,1 | 8,0 | 7,7 | 8,2 | 35,0 | 8,8 | 123,2 | 64,0 | 59,3 | 67,2 | |
| 210 м | 6,5 | 7,0 | 6,7 | 6,5 | 26,7 | 6,7 | 42,3 | 49,0 | 44,9 | 42,3 | |
| 21 км | 10 м | 28,4 | 30,1 | 26,2 | 24,1 | 108,8 | 27,2 | 806,6 | 906,0 | 686,4 | 580,8 |
| 110 м | 8,3 | 8,5 | 9,2 | 7,4 | 33,4 | 8,4 | 68,9 | 72,3 | 84,6 | 54,8 | |
| 210 м | 5,5 | 6,2 | 6,4 | 5,7 | 23,8 | 6,0 | 30,3 | 38,4 | 41,0 | 32,5 | |
|
| 140,0 | 141,4 | 132,6 | 132,2 | 546,2 | ||||||
 = 546,2;
 = 15,2;
= 12294,1
|
Первоначальная обработка данных дисперсионным анализом двухфакторного опыта по изучению накопления свинца в зерне яровой пшеницы в зависимости от удаления посевов от города Омска и от автомагистрали
4. Находим суммы квадратов отклонений по формулам таблицы 10:
а) общей дисперсии SSY
SSY = 
;
б) дисперсии вариантов SSV
SSV = 
= (48903 – 
): 4 = 3938,6;
в) дисперсии повторений SSP
SSP = 
= (74654 – 
): 9 = 7,8.
г) остаточной дисперсии SSZ
SSZ = SSY –(SSV+ SSP) = 4007,0 – (3938,6+7,8) = 60,6
Таким образом, на долю варьирования вариантов приходится 98,3% от величины общего варьирования ((3938,6: 4007,0)·100%). Дисперсионный анализ позволил установить, что изучаемые факторы существенно влияют на содержание свинца в зерне яровой пшеницы, однако влияние каждого фактора в отдельности и степень взаимодействия этих факторов на изучаемый показатель на данном этапе не установлено. Если визуальный анализ полученных результатов позволяет нам предположить, что удалённость от автомагистрали действительно существенно влияет на содержание свинца в зерне пшеницы, то анализ влияния удалённости от города на качество зерна пшеницы не позволяет нам достоверно судить о каком-либо изменении концентрации тяжёлого металла в зерне без дальнейшей статистической обработки данных для выявления главных эффектов и взаимодействия факторов.
5. Поэтому следующий этап статистической обработки многофакторного комплекса (в нашем случае – двухфакторного) заключается в определении так называемых главных эффектов изучаемых факторов и их взаимодействия. С этой целью составляют таблицу сумм и средних урожаев по градациям изучаемых факторов (таблица 26). В данную таблицу (в нашем случае 3х3) вписывают суммы значений по вариантам, и находят необходимые для расчёта главных эффектов суммы по факторам А и В.
Сумму квадратов отклонений исследуемого фактора (SSA, SSB и т.д.) вычисляют по формулам:
для фактора А:
SSV(А) = 
; (43)
где 
- сумма квадратов суммированных по повторениям значений признака по фактору А;
- количество вариантов по фактору В в опыте;
Таблица 15
Суммы значений содержания свинца в зерне яровой пшеницы
для определения главных эффектов и взаимодействия факторов
| Факторы | Суммированные по повторениям значения
| Суммы значений по фактору А
| ||
| 10 м от автомагистрали | 110 м от автомагистрали | 210 м от автомагистрали | ||
| 1 км от города | 132,2 | 42,0 | 28,6 | 202,8 |
| 11 км от города | 115,7 | 35,0 | 26,7 | 177,4 |
| 21 км от города | 108,8 | 33,4 | 23,8 | 166,0 |
Суммы значений по фактору В
| 356,7 | 110,4 | 79,1 | 546,2 |
для фактора В:
SSV(В) = 
; (44)
где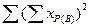 
- сумма квадратов суммированных по повторениям значений признака по фактору В;
- количество вариантов по фактору А в опыте.
Таким образом, получаем:
SSV(А) = = ((202,82 + 177,42 + 166,02) – 
): 4 · 3 = (100154,6 – 99441,8): 12 = 59,4
SSV(В) = = ((356,72 + 110,42 + 79,12) – ): 4 · 3 = (145679,9 – 99441,8): 12 = 3853,2
Сумму квадратов отклонений для вычисления взаимодействия исследуемых факторов А и В (SSV(АВ))находят в результате вычитания из общей суммы квадратов отклонений для вариантов (SSV)суммы квадратов отклонений для главных факторов (SSV(А) + SSV(В)):
SSV(АВ) = SSV – (SSV(А) + SSV(В)) = 3938,6 – (59,4 + 3853,2) = 26,0
6. Результаты полученных вычислений записываем в сводную таблицу дисперсионного анализа (таблица 27).
При заполнении таблицы необходимо учесть число степеней свободы (df) для каждого вида дисперсии. Число степеней свободы при расчёте общей дисперсии, дисперсии всех вариантов, повторений и остаточной дисперсии рассчитывается по формулам приведённым в таблице 16. Число степеней свободы для каждого изучаемого фактора (А и В) равно числу вариантов этого фактора минус единица: (nV(A) – 1) или (nV(В) – 1).
Таблица 16
Результаты дисперсионного анализа двухфакторного полевого опыта
| Дисперсия | Сумма квадратов отклонений, SS | Число степеней свободы, df | Дисперсия,
| Критерий Фишера, F | ||
| фактическое | табличное | |||||
| Общая Повторений Вариантов Удалённости от города (А) Удалённости от дороги (В) Взаимодействия (АВ) | 4007,0 7,8 3938,6 59,4 3853,2 26,0 | – – 492,3 29,7 1926,6 6,5 | – – 129,6 7,81 507,0 1,71 | – – 2,6 3,6 3,6 3,0 | – – 3,9 6,2 6,2 4,8 | |
| Остаточная | 60,6 | 3,8 |
Стандартные значения критерия Фишера (F05 или F01) берут из приложения III, исходя из числа степеней свободы для дисперсии главных эффектов А, В и взаимодействия АВ (числитель) и 16 степеней свободы дисперсии остатка (знаменатель). О том как установить табличное значение критерия Фишера подробно изложено в предыдущей главе на страницах 48-49.
Таким образом, устанавливаем, что на пересечении числа степеней свободы для меньшей дисперсии (в нашем случае остаточная, df = 16) и числа степеней свободы для большей дисперсии вариантов (df = 8), устанавливаем, что F05 для вариантов в целом составляет 2,6, F01 – 3,9, что свидетельствует об высоком и достоверном влиянии изучаемых факторов (близость к источником техногенного загрязнения) на накопление свинца в зерне яровой пшеницы. Изучая, каждый из факторов в отдельности, можно свидетельствовать с вероятностью не ниже 99% (F01 < FФ), что каждый из них оказал влияние на результирующий признак, то есть имел достоверное влияние. Достоверного взаимодействия между изучаемыми факторами не установлено, поэтому можно констатировать только раздельное влияние удалённости от источников техногенного загрязнения на накопление свинца в зерне пшеницы.
Анализируя фактическое распределение сумм квадратов отклонений, можно уверенно констатировать тот факт, что на накопление свинца в зерне пшеницы в первую очередь оказал фактор удалённости от автомагистрали. Долю влияния фактора, можно рассчитать по отношению суммы квадратов отклонений изучаемого фактора (SSV(A) или SSV(B)) к сумме квадратов отклонений вариантов (SSV). Так, доля влияния фактора А составила лишь 1,5% (59,4: 3938,6 · 100%), в то время как доля влияния фактора В была основной и составила 97,8% (3853,2: 3938,6 · 100%).
Соответственно, можно судить о том, что повышение накопления свинца в зерне яровой пшеницы на 97,8% обусловлено приближённостью посевов к автомагистрали, и лишь на 1,5 % - их приближённостью к черте города.
7. Последующим этапом определения достоверности изучаемых факторов на результирующий признак является оценка существенности частных различий.
Абсолютная и относительная ошибка средних (
и 
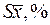) рассчитываются по формулам 20 и 21. Стандартное отклонение 
в дисперсионном анализе определяется как корень из остаточной дисперсии. Таким образом, получаем:
,
Это означает, что мы можем утверждать, что среднее содержание свинца в зерне яровой пшеницы варьирует в среднем на 0,97 мг/кг.
Оценка конкретных различий между средними осуществляется с помощью критерия t, фактическое значение которого представляет собой отношение разности средних d (среднее изменение урожайности или другого наблюдения под действием изучаемых факторов) к ошибки разности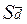 
, которая рассчитывается, как уже описывалось ранее, по формуле:
Оценить достоверность влияния изучаемых факторов в совокупности наиболее целесообразно вычислением критерия существенности НСР при вероятности в 95 или 99%.
.
Для нашего случая величина НСР при 95%-ной вероятности и числе степеней свободы остаточной дисперсии равной 16, составит:
мг/кг.
То есть, если в опыте полученные разности между средними (прибавка или снижение содержания свинца в зерне.) будут выше или равны 2,88 мг/кг, только в этом случае мы можем утверждать, что это изменение доказано с вероятностью в 95%.
При 99%-ной вероятности величина НСР будет выше:
мг/кг.
8. В завершении проведения дисперсионного анализа многофакторного опыта (в нашем случае – двухфакторного) проводим оценку существенности главных эффектов и взаимодействия факторов по показателю НСР05. В рассматриваемом примере частные средние опираются на число повторений (nP) равное 4, а средние для главного эффекта по фактору А на произведение числа повторений и количества вариантов по фактору В (np·nV(B)), то есть 4 · 3 = 12 наблюдений. Вычисляем Sd и НСР05 или НСР01 для главных эффектов по формулам:
для фактора А:
; (45)
;
для фактора В:
Рассчитывать 
и НСР05 для взаимодействия факторов А и В в приведённом примере не нужно, поскольку не установлено достоверного влияния этого взаимодействия на результативный признак.
Поскольку в нашем случае количество вариантов по каждому фактору было одинаковым, величина ошибки разности и НСР также будут одинаковыми.
9. В заключение составляют итоговую таблицу (табл. 17). В таблице показывают три значения НСР05; одно для оценки существенности частных различий между средними (НСР05 = 3,97 мг/кг), а два других для оценки существенности разности средних по фактору А и по фактору В (НСР05 = 1,68 мг/кг), то есть оценки главных эффектов удалённости посевов яровой пшеницы от источников техногенного загрязнения.
Анализируя, полученные результаты можно смело констатировать тот факт, что удаление от автодороги посевов яровой пшеницы существенно снижает содержание свинца в зерне, в то время как удаление от черты города посевов ведёт к снижению содержания свинца во многих случаях весьма незначительно, или вообще отсутствует эффект от территориальной удалённости посевов от города. Анализ частных изменений содержания свинца в зерне пшеницы в зависимости от расположения посевов позволит более детально проанализировать полученные данные, однако в данном разделе мы не будем заострять на этом внимание.
Таблица 17
Влияние расположения посевов яровой пшеницы от источников техногенной нагрузки на накопление свинца в зерне
| Фактор В Фактор А | Содержание Pb в зерне яровой пшеницы | Средние по фактору А НСР05 = 1,68 мг/кг | ||
| 10 м от автомагистрали | 110 м от автомагистрали | 210 м от автомагистрали | ||
| 1 км от города | 33,1 | 10,5 | 7,2 | 16,9 |
| 11 км от города | 28,9 | 8,8 | 6,7 | 14,8 |
| 21 км от города | 27,2 | 8,4 | 13,9 | |
| Средние по фактору В НСР05 = 1,68 мг/кг | 29,7 | 9,2 | 6,6 |
НСР05 = 3,97 мг/кг для сравнения частных средних
1.3. Методы определения связи между признаками:
Корреляция и регрессия
В практике сельскохозяйственных и биологических исследований часто возникает необходимость изучить характер связи между двумя (или более) варьирующими признаками или свойствами растений. Многие признака и свойства растений находятся между собой в определённой взаимосвязи. Некоторые из них являются взаимосвязанными, другие – изменяются в определённом направлении под влиянием общих условий. Примером связи первого типа может служить часто наблюдаемая положительная зависимость между удельной массой корневой системы в общей биомассе растений и урожайностью исследуемой зерновой культуры. С другой стороны, мощная корневая система развивается при хорошей обеспеченности растений фосфором на первых этапах их роста и развития. Таким образом, можно предположить, что фосфорные удобрения, способствуя развитию корневой системы, повлекут увеличению урожайности зерновых. А значит, между обеспеченностью растений фосфором и урожайностью будет отмечаться зависимость.
Исследование корреляции сводится к следующему.
1. Устанавливают факт зависимости изменений одного признака от изменения другого и определяют форму связи между ними. Корреляцию называют простой, если исследуется связь между двумя признаками, или множественной, когда на величину одного результативного признака влияют несколько факториальных. Как правило, в сельскохозяйственных и биологических исследованиях на результативный признак отмечается влияние нескольких факториальных, однако далеко не всегда удаётся учесть все факторы и поэтому приходиться изыскивать наиболее вероятно влияющий факториальный признак.
В зависимости от характера изменений результативного признака под влиянием факториального различают:
а) линейную корреляцию, когда с увеличением среднего значения одного признака также увеличивается среднее значение другого (прямая корреляция), или с увеличением среднего значения одного признака уменьшается среднее значение другого (обратная корреляция);
б) криволинейную корреляцию: при возрастаний значений одного признака другой возрастает неравномерно или принимает значения, возрастающие до определённой величины, а затем убывающие, или наоборот. Этот тип корреляции также бывает прямым и обратным.
2. Находят тесноту связи, то есть степень сопряжённости между значениями одного и другого признака. Степень сопряжённости обычно выражают в виде отвлечённого числа, которое при линейной корреляции называют коэффициентом корреляции, а при криволинейной зависимости – корреляционным отношением.
Линейный коэффициент корреляции. Как было сказано ранее, для характеристики линейной корреляции между двумя признаками вычисляют особый показатель коэффициент корреляции. Для того, чтобы более полно понять, что такое корреляционная зависимость, рассмотрим пример (таблица 18), по наличию связи между дозой азотного удобрения (кг д.в./га), вносимого под ячмень и содержанием белка в зерне (%)
Таблица 18
Содержание белка в зерне ярового ячменя в зависимости
от дозы азотного удобрения
| Доза азотного удобрения, кг д.в./га X | Содержание белка в зерне, % Y | Доза азотного удобрения, кг д.в./га X | Содержание белка в зерне, % Y |
| 0 (контроль, б/у) | 10,4 | 13,4 | |
| 10,2 | 13,9 | ||
| 10,9 | 13,7 | ||
| 10,4 | 13,9 | ||
| 11,9 | 14,1 | ||
| 11,5 | 14,0 | ||
| 11,5 | 14,1 | ||
| 12,8 | 14,3 | ||
| 12,3 | 14,7 | ||
| 12,9 | 14,9 | ||
| 12,8 | 14,6 | ||
| 12,8 | 14,8 | ||
| 13,2 | 14,9 | ||
| 13,7 | 15,2 | ||
| 13,3 | 15,2 |
В теоретической статистике доказывается, что коэффициент корреляции определяется индивидуальными отклонениями значений признаков от их средних значений, а соответственно обусловлен средними квадратическими отклонениями распределений. Вычисляют его несколькими способами, но классическим считается расчёт линейного коэффициента корреляции по следующей формуле:
(46).
Числитель этой формулы – сумма произведений отклонений x и y от своих средних значений 
и 
. В знаменателе 
и 
- средние квадратические отклонения распределений х и у, n – число сопоставимых пар.
При отсутствии корреляции, то есть если признаки варьируют независимо друг от друга, любое из значений 
может сочетаться как с положительными, так и с отрицательными 
одинаково часто. Следует предпологать, что в достаточно больших совокупностях положительных произведений 
будет столько же сколько и отрицательных, и сумма произведений будет равна или почти равна нулю.
Если признаки варьируют сопряжено, то отклонения 
будут сочетаться не с любыми, а только с некоторыми отклонениями . В случае прямой корреляции положительные отклонения 
будут преимущественно сочетаться с положительными, а отрицательные 
- с отрицательными 
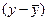. Иначе говоря, произведение отклонений будут преимущественно однозначными и сумма их – положительной. При обратной корреляции сочетаются преимущественно отклонения с разными знаками, и сумма их произведений будет отрицательна. В том и в другом случаях сумма произведений будет тем больше, чем меньше будет независимых сочетаний отклонений, то есть чем больше будет сопряжённость между варьирующими признаками.
Упрощение приведённой формулы (64) математическим преобразованием даст другую формулу:
(47).
Произведя расчёт по итоговым значениям исходных переменных, линейный коэффициент корреляции можно определить, минуя вычисление средних квадратичных отклонений по формуле:
(48) или
(49).
Наиболее удобной для расчётов, проводимых в условиях отсутствия достаточно мощной вычислительной техники, представляется формула 44.
Коэффициент корреляции может принимать значения от +1 до -1 в зависимости от тесноты и направленности связи.
Общепринятая степень тесноты связи отражена в таблице 30.
Таблица 19
Количественные критерии оценки тесноты связи
| Величина коэффициента корреляции | Характер связи |
| ±0–0,1 | отсутствует |
| ±0,1–0,3 | очень слабая |
| ±0,3–0,5 | слабая |
| ±0,5–0,7 | умеренная |
| ±0,7–0,9 | сильная |
| ±0,9–1,0 | очень сильная |
Если коэффициент корреляции имеет положительный знак (например, r = 0,75), то связь прямая и с увеличением значения факторного признака х увеличивается значение результативного признака у. Если r отрицательный (например, r = – 0,83), то связь обратная и с увеличением значения факторного признака х уменьшается значение результативного признака у. При r = 1,0 говорят о наличии функциональной связи между изучаемыми признаками.
Ошибка коэффициента корреляции при осуществлении выборки из нормальной совокупности рассчитывают по формуле:
(50).
где r – коэффициент корреляции
n – выборка из генеральной совокупности (число пар (дат) наблюдений изучаемых признаков).
В классической статистике принято записывать значение коэффициента корреляции вместе с его ошибкой в виде r ± Sr. Однако, современные статистические методы предполагают определение скорректированного коэффициент корреляции, который определяется по формуле:
(51),
где radj – скорректированный коэффициент корреляции,
p – число параметров статистического исследования (число независимых переменных плюс 1, так как в модель включён свободный член).
При достаточно большом числе наблюдений (не менее 100) коэффициент корреляции можно считать существенным, если он превышает свою ошибку в 3 и более раза, то есть если 
>3.
В малочисленных выборках существенность коэффициента корреляции оценивают с помощью известного критерия t. В этом случае
, (52)
где n – число парных наблюдений.
Сопоставление фактического и табличного t при числе степеней свободы df = (n-2) даёт возможность оценить существенность r при избранном уровне значимости.
