При рассмотрении данных любого опыта (например, приведённых в таблицах 1 и 5) не трудно заметить большее или меньшее варьирование данных урожайности. Даже при самой тщательной работе урожаи на параллельных делянках или сосудах получаются не совсем одинаковыми. На величине урожая сказываются все те многочисленные работы, которые были проведены для его получения.
Дробный метод
Этот метод в отдельных случаях может применяться для обработки результатов вегетационных опытов, в которых отсутствует связь между сравниваемыми вариантами – сосудами (независимые, несопряжённые выборки), а также полевых экспериментов и лабораторных анализов, когда ошибки средних арифметических вычисляются на основании большого числа наблюдений (большие выборки, n>30). При обработке результатов полевого опыта этот метод можно использовать только в случае отсутствия систематических ошибок.
Обработка ведётся в следующей последовательности:
1. Составляют таблицу урожаев и вычисляют среднюю арифметическую величину по каждому варианту, для чего складывают конкретные исследуемые величины по всем повторениям каждого отдельного варианта и эту сумму делят на число повторений (
, 
, 
… 
).
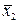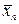2. Находят отклонения поделяночных урожаев от среднего урожая по варианту (
). Показатели каждой повторности варианта отличаются от их среднего значения и могут быть больше или меньше его. Поэтому отклонения показателей конкретных повторностей от среднего их значения могут быть положительными или отрицательными. Таким образом получают индивидуальные отклонения от средней величины для каждого конкретного варианта по всем повторностям: (
),(
)…(
). Правильность вычислений проверяют по равенству 
, незначительное отклонение может быть лишь результатом округления и не должно превышать 2% от абсолютного исследуемого показателя.
3. Находят квадраты отклонений ()2 и их суммы по каждому варианту в отдельности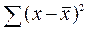 
. Кроме того, весьма целесообразно для изучения размера вариативности и упрощения дальнейших расчётов определить среднее квадратичное (стандартное) отклонение для каждого отдельно варианта, по одной из приведённых выше формул (11-14). Как правило, при достаточно большом числе повторений (≥4), 68,3% показаний находятся в пределах 
; 95,2% в пределах 
; 99,7% в пределах – 
, а за этими пределами появление наблюдений маловероятно. О размере вариативности показателя в пределах одного варианта позволяет судить величина коэффициента вариации, определяемая по формуле:
V = 
(19),
где V – коэффициент вариации, %.
Коэффициент вариации показывает относительную величину варьирования показателя. Так, колеблемость считается незначительной, если коэффициент вариации не более 10%, средний – при 10-20% и значительной – если V больше 20%. При превышении коэффициента вариации 35%, говорят о том, что средняя не типична для изучаемой совокупности делянок или сосудов в пределах одного варианта и использовать её в дальнейших расчётах без корректировки нельзя.
4. Далее рассчитывают абсолютную и относительную ошибки средних арифметических по вариантам. Обычно вычисление абсолютной средней ошибки производят по формуле, объединённой с формулой для среднего квадратичного отклонения:
(20).
Если расчет стандартного отклонения уже проведён, то расчет ошибки средней арифметической осуществляют по формуле:
(21),
где 
- стандартное (среднее квадратичное) отклонение.
Величина ошибки среднего арифметического значения уменьшается при доброкачественном выполнении опыта, правильном выборе участка под опыт и при увеличении числа повторений каждого варианта.
Относительная ошибка средней арифметической, представляет собой отношение абсолютной её ошибки к величине среднего арифметического значения показателя, и выражается в процентах:
(22).
Также, как и величина абсолютной ошибки среднего арифметического значения, относительная ошибка показывает точность исполнения опыта или анализа и чем меньше её значение, тем более доброкачественно был поставлен эксперимент или проведён анализ. Одним из путей снижения этой ошибки является увеличение числа повторностей каждого изучаемого варианта. Относительная ошибка средней арифметической в пределах 1-2% является отличной для всех полевых опытов; не превышающей 3% - хорошей; от 3 до 5% -умеренной, не выше 8% - удовлетворительной. При её превышении 8% порога, следует учесть недоброкачественность выполнения эксперимента или анализа или малое количество повторений в опыте. В этом случае, необходимо, по возможности, откорректировать полученный материал или даже забраковать вариант. В вегетационных опытах с удобрениями ошибка средней при соответствующей правильной методике их выполнения, как правило, на 2-3% ниже, чем в полевых и считается нормальной если она не превышает 2-3%.
5. Далее определяют разности между средними показателями сравниваемых вариантов. Сравнение, как правило, проводят с контрольным вариантом:
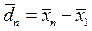(23) или же сравнивают между собой какие-либо другие варианты, например, для установки целесообразности совместного внесения под ячмень (табл. 1) азотно-фосфорного удобрения по сравнению с раздельным внесением азота и фосфора:
(24),
где 
– разность между сравниваемыми вариантами;
, , 
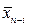– средние арифметические сравниваемых вариантов (некоторого (n), контрольного (1), сравниваемого (n-i)).
i ( 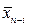) – числовое значение (1, 2, 3…) показывающее удалённость по схеме варианта сравнения от изучаемого варианта.
6. Следующим шагом является определение ошибки разности между двумя средними (сравниваемыми вариантами). Существенность различий между числовыми показателями вариантов опыта зависит от того, какие ошибки имеют средние арифметические значения показателей сопоставляемых вариантов. Чем больше разница между вариантами превосходит сумму ошибок, тем больше будет достоверность (надёжность) этой разницы. Разность между показателями сопоставляемых вариантов имеет ошибку, которую называют ошибкой разности 
и вычисляют по формуле:
(25), если вариант, с которым проводят сравнение – контрольный, или по формуле:
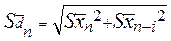, (26) при сравнении с некоторым вариантом n-i.
6. Заключительным этапом расчёта дробным методом является вычисление существенности разности. Существенность различий между 
и 
или и 
оценивают по отношению разности 
или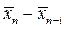 
к её ошибке . Это отношение называется критерием существенности разности, или критерием Стьюдента (t):
(27)
Критерий Стьюдента (t) показывает, во сколько разность показаний вариантов больше ошибки разности и является мерой достоверности. Чем больше величина t, тем больше достоверность разности и надёжность выводов и рекомендаций, основанных на результатах опыта.
Пример. Проведём статистическую обработку данных полевого опыта с ячменём дробным методом (табл. 6).
Итак, в опыте установили положительное влияние на урожайность ячменя азотного, фосфорного удобрения и их сочетаний, в том числе и совместно с калийными удобрениями. Однако, мы не можем утверждать эффективность совместного внесения азотно-фосфорных удобрений (N60P60) по сравнению с их раздельным внесением (N60 или P60), а также говорить о положительной роли на урожайность ячменя включение в состав удобрительной смеси калия в дозе 60 кг/га. Для утверждения или отрицания наших предположений, необходимо сопоставить между собой варианты N60P60 и N60, N60P60 и P60, а также N60P60К60 и N60P60.
Мы не станем вновь приводить расчёты, и интерпретируем только полученные по этим сопоставляемым вариантам меняющиеся результаты:
а) при сопоставлении варианта N60P60 и N60 разность урожаев d составила 0,25 т/га, ошибка разности Sd – 0,13, критерий t – 1,88;
б) при сопоставлении варианта N60P60 и P60 разность урожаев d составила 0,38 т/га, ошибка разности Sd – 0,13, критерий t – 2,82;
в) при сопоставлении варианта N60P60К60 и N60P60 разность урожаев d составила -0,06 т/га, ошибка разности Sd – 0,13, критерий t – 0,5.
Исходя из полученных результатов, можно смело утверждать приоритетное влияние на урожайность ячменя азотного удобрения в дозе 60 кг/га. Доказать целесообразность добавления к азотному удобрению фосфорного, при возделывании ячменя, с требуемой степенью вероятности 95% не удалось. Не установлено и положительного действия на урожайность культуры калийных туков. Отсюда, можно констатировать тот факт, что, не оперируя полученным качеством зерна, для достижения максимально эффективной прибавки урожая ячменя в условиях закладки опыта целесообразно внесение исключительно азотного удобрения в дозе 60 кг/га.
Таблица 6
Статистическая обработка данных в опыте по изучения влияния минеральных удобрений
на урожайность ячменя дробным методом, сорт Омский 90
| Вариант | Повторность n | Урожайность ячменя, т/га x | Средняя урожайность ячменя, т/га
| Отклонение от среднего по варианту 
| Квадрат отклонений
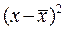
| Стандартное отклонение
| Коэффициент вариации V,% | Ошибка среднего | Разность в урожаях d | Ошибка разности
| Критерий существенности tфакт | Стандартные значения t tтеор | |
абсолютная
| относительная
| ||||||||||||
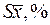
| I Контроль (без удобрений) | 2,51 | 2,45 | 0,06 | 0,0036 | 0,13 | 5,17 | 0,06 | 2,59 | – | – | – | – | |
| 2,34 | -0,11 | 0,0121 | |||||||||||
| 2,60 | 0,15 | 0,0225 | |||||||||||
| 2,35 | -0,10 | 0,0100 | |||||||||||
| Σ | 9,80 | 0,00 | 0,0482 | ||||||||||
| II N60* | 2,95 | 2,87 | 0,08 | 0,0064 | 0,12 | 4,01 | 0,06 | 2,01 | 0,42 | 0,09 | 4,90 | 2,40 | |
| 2,72 | -0,15 | 0,0225 | |||||||||||
| 2,97 | 0,10 | 0,0100 | |||||||||||
| 2,84 | -0,03 | 0,0009 | |||||||||||
| Σ | 11,48 | 0,00 | 0,0398 | ||||||||||
| III P60 | 2,80 | 2,74 | 0,06 | 0,0036 | 0,10 | 3,72 | 0,06 | 2,15 | 0,29 | 0,08 | 3,55 | 2,40 | |
| 2,60 | -0,14 | 0,0196 | |||||||||||
| [2,83] | 0,09 | 0,0081 | |||||||||||
| 2,74 | 0,00 | 0,0000 | |||||||||||
| Σ | 10,97 | 0,01 | 0,0313 |
окончание таблицы 6
| IV N60P60 | 3,05 | 3,12 | -0,07 | 0,0049 | 0,24 | 7,76 | 0,12 | 3,88 | 0,67 | 0,13 | 5,11 | 2,40 | |
| 3,45 | 0,33 | 0,1089 | |||||||||||
| 3,12 | 0,00 | 0,0000 | |||||||||||
| 2,87 | -0,25 | 0,0625 | |||||||||||
| Σ | 12,49 | 0,01 | 0,1763 | ||||||||||
| V N60P60K60 | 3,00 | 3,06 | -0,06 | 0,0036 | 0,06 | 2,08 | 0,03 | 1,04 | 0,61 | 0,13 | 4,87 | 2,40 | |
| 3,04 | -0,02 | 0,0004 | |||||||||||
| 3,15 | 0,09 | 0,0081 | |||||||||||
| 3,05 | -0,01 | 0,0001 | |||||||||||
| Σ | 12,24 | 0,00 | 0,0122 |
*Пример расчётов на варианте N60:
1. 
2. 
3. V = = 
4. = 
5. 
6. 
7. 
8. 
Обобщённый метод
Большое количество квадратических ошибок, получаемых в дробном методе, нередко указывает на необходимость характеризовать точность опыта при помощи одной средней ошибки. Это возможно при использовании обобщённого метода обработки экспериментальных результатов. Этот метод зачастую повышает надёжность сравнения двух средних по вариантам, так как вычисляется обобщённая ошибка в целом для опыта, которая затем используется для характеристики существенности. Величина обобщённой ошибки вычисляется по значительно большему числу показателей и нередко бывает более точной.
Первоначально расчёты в этом методе такие же, как и в дробном методе: вычисляют для каждого варианта его среднюю, находят отклонения отдельных определений для каждого варианта от его средней, возводят эти отклонения в квадрат. Далее, можно определить стандартное отклонение и коэффициент вариации, но в принципе это делать необязательно. Следующим шагом в обобщённом методе обработки является суммирование всех квадратов отклонений 
или стандартных (средних квадратичных) отклонений 
. Среднюю квадратичную ошибку для всех вариантов опыта в целом (обобщённую ошибку) рассчитывают по формуле:
(28)
где nP ·nl – общее число всех сосудов, делянок или других наблюдений.
Относительную ошибку опыта 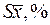определяют также, как и в дробном методе.
При обобщённой обработке результатов опыта для всех вариантов опыта имеем одинаковые ошибки средних. Следовательно, ошибка опыта, или разности средних, будет равна
(29)
Критерий существенности разности t определяют также, как и в дробном методе путём деления разности между вариантами на её ошибку.
Достоверность полученных в опыте разностей оценивают по критерию НСР (наименьший средний результат) с достоверностью 95%, иногда, значительно реже, с достоверностью 99%. Рассчитывают НСР по формуле:
(30),
таким образом при оценке достоверности опыта с уровнем вероятности 0,95 формула примет вид:
,
а при уровне вероятности 0,99 –
Число степеней свободы определяют аналогично, как и в дробном методе: 
.
Использование такого показателя, как наименьший средний результат (НСР05), позволяет без труда установить эффективность любых видов минеральных удобрений. Если разность показателей сопоставимых вариантов превышает НСР05, то можно смело утверждать о доказанности влияния изучаемого фактора. В изучаемом нами примере, все прибавки от применения различных сочетаний туков превышали НСР05, что свидетельствует о достоверном их влиянии.
Разностный метод
Если в опыте урожаи в различных повторностях были разновелики вследствие различного исходного плодородия, то иногда может быть применим разностный метод обработки результатов. Сущность этого метода заключается в определении ошибки средней разности, а не разности средних как в дробном и обобщённом методах. Разностный метод предусматривает сравнение сопряжённых, коррелирующих пар, что позволяет в значительной степени устранить систематическую ошибку, вызванную различным плодородием в разных повторениях полевого опыта.
Техника вычислений в разностном методе заключается в следующем:
1. Для каждой повторности определяют разность (d) урожаев между сравниваемыми вариантами (парами, из-за чего метод иногда называют парным).
2. Находят среднюю разность (
) по формуле средней арифметической простой, разделив сумму разностей всех повторений одного варианта на количество повторений в этом варианте.
3. Определяют отклонения от средней разности 
, квадраты этих отклонений 
и их сумму 
.
4. Вычисляют ошибку средней разности, по формуле идентичной расчёту ошибки средней арифметической:
(31)
Таким образом, последовательность расчётов сохраняется, как и при обработке обычного вариационного ряда.
Рассчитанная ошибка средней разности служит для оценки существенности разности по критерию t, который определяют также как и в дробном или обобщённом методах. Теоретическое значение критерия t находим в приложении 2 для числа степеней свободы 
.
Этот способ вычисления единственный пригодный в случае закономерного изменения урожайностей по повторениям, однако недостатком его является то, что ошибка разности подсчитывается по малому числу наблюдений.
Таблица 9
Статистическая обработка данных в опыте по изучения влияния минеральных удобрений на урожайность ячменя разностным методом
| Повторение | Урожайность по повторениям, т/га | Отклонение от средней урожайности
| Квадрат отклонений от средней урожайности
| Разность, d | Отклонение от средней разности
| Квадрат отклонений
от средней разности
|
| P60 | ||||||
| 2,80 | 0,22 | 0,051 | – | – | – | |
| 2,60 | 0,02 | 0,001 | – | – | – | |
| 2,50 | -0,08 | 0,006 | – | – | – | |
| 2,40 | -0,18 | 0,031 | – | – | – | |
 = 2,58  =0,088 
| ||||||
| N60P60 | ||||||
| 3,05 | 0,19 | 0,038 | 0,25 | -0,03 | 0,0009 | |
| 2,90 | 0,04 | 0,002 | 0,30 | 0,02 | 0,0004 | |
| 2,75 | -0,11 | 0,011 | 0,25 | -0,03 | 0,0009 | |
| 2,72 | -0,14 | 0,020 | 0,32 | 0,04 | 0,0016 | |
 = 2,86
| = 0,071
| 
| ||||
| ||||||
при расчёте разностным методом:
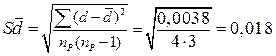t = 0,28 / 0,018 = 15,6 при t05 = 3,2
|
Дисперсионный анализ
В настоящее время общепринятым методом статистической обработки данных полевого опыта является дисперсионный анализ (или анализ рассеяния), заключающийся в выявлении роли и значения разных источников варьирования, в том числе и случайных ошибок, в общей изменчивости опыта. Это осуществляется путём разложения общей дисперсии поделяночных урожаев (или других данных) на составные части.
Дисперсионный анализ по сравнению с дробным и другими рассмотренными выше методами даёт возможность установить влияние всего комплекса факторов (изучаемых приёмов, плодородия почвы, случайных ошибок) и степень влияния каждого фактора в отдельности на изменчивость изучаемого признака (например, урожая в полевом опыте). В основе этого метода лежат следующие предпосылки:
При обработке данных вегетационных опытов (несопряжённые данные), общая изменчивость результативного признака СY, расчленяется только на варьирование между выборками (вариантами) СV и внутри выборок (между повторениями) СZ. Следовательно, в общей форме изменчивость признака может быть представлена выражением:
При обработке данных полевых опытов, когда опытные данные варьируют зависимо друг от друга (сопряжённые данные), т.е. варианты в полевом опыте связаны с наличием повторений, общее варьирование результатов обусловлено влиянием изучаемых факторов (особенностями вариантов), различием в плодородии почвы отдельных повторений и действием случайных ошибок в опыте:
Из общего варьирования СY можно вычленить варьирование, обусловленное влиянием изучаемых факторов СV, различием в плодородии почвы СP и выявить случайное варьирование СZ, характеризующее ошибки опыта, от которых зависит его точность:
При дисперсионном анализе можно использовать несколько математических методов (моделей), различающихся между собой расчётом сумм квадратов отклонений для разных видов варьирования и соответственно объёмом вычислительной работы.
