Статистическая обработка однофакторного полевого опыта с повторностями заключается в расчленении общего варьирования (дисперсии) поделяночных урожаев на три составные части. Из общей дисперсии исключают дисперсии, характеризующие варьирование: а) изучаемого фактора (варианта, например, дозы удобрений) и б) контролируемого фактора, которым в полевом опыте является повторность с полным набором делянок всех вариантов, занимающая определённую часть опытного участка со свойственным её почвенным плодородием. Остаточная дисперсия (общая дисперсия минус дисперсия вариантов и минус дисперсия повторения) характеризует случайные ошибки опыта. Понятно, что чем меньше будет остаточная дисперсия, тем меньше в опыте случайных ошибок, тем он точнее.
Как известно из предыдущего, варьирование любой величины характеризует дисперсия, представляющая собой частное от деления суммы квадратов отклонений от средней на число степеней свободы, то есть
 .
.
Применительно к анализу данных однофакторного полевого опыта суммы квадратов и числа степеней свободы находят аналогично, но формулы для расчёта упрощены и преобразованы до следующего вида (табл. 10).
Таблица 10
Формулы для вычисления показателей дисперсии
| Вид дисперсии | Суммы квадратов отклонений, SS | Числа степеней свободы, df |
1. Общая 
| 
|  (33) (33)
|
2. Вариантов 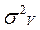
| 
|  (34) (34)
|
3. Повторений 
| 
|  (35) (35)
|
4. Остаточная 
| СZ = СY – (СV + СP). |  (36) (36)
|
В формулах таблицы 10 обозначают:
 – общая сумма поделяночных урожаев (или других наблюдений) в опыте;
– общая сумма поделяночных урожаев (или других наблюдений) в опыте;
 - сумма квадратов поделяночных урожаев (или других наблюдений) в опыте;
- сумма квадратов поделяночных урожаев (или других наблюдений) в опыте;
 – сумма квадратов урожаев (или других наблюдений) всех делянок варианта;
– сумма квадратов урожаев (или других наблюдений) всех делянок варианта;
 – сумма квадратов урожаев (или других наблюдений) всех делянок повторения;
– сумма квадратов урожаев (или других наблюдений) всех делянок повторения;
nV – число вариантов;
nP – число повторений.
Многие исследователи предлагают использовать при дисперсионном анализе корректирующий фактор СK, который позволяет несколько упростить расчёты и представляет собой отношение квадрата суммы значений всех поделяночных наблюдений на их количество:
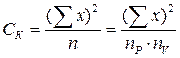 (39).
(39).
Таким образом, общая сумма квадратов отклонений примет вид:
 (40).
(40).
Для использования корректирующего фактора при расчётах квадратов отклонений по вариантам (41) и повторениям (42) формулы необходимо преобразовать, разделив каждое значение числителя на знаменатель:
 (41);
(41);
 (42).
(42).
Существенного упрощения подобные преобразования не дают, поэтому каждый исследователь может пользоваться той формулой, которая ему кажется наиболее простой.
Пример. Проведём статистическую обработку данных однофакторного полевого опыта с ячменём дисперсионным анализом.
Для дисперсионного анализа необходимо составить таблицу, (табл. 11). Анализ проводят в следующей последовательности.
1. После перенесения из журнала данных урожаев (или других наблюдений) в таблицу 11 подсчитывают суммы урожаев всех повторений для каждого варианта  и суммы урожаев всех вариантов для каждого повторения
и суммы урожаев всех вариантов для каждого повторения  при этом сумма всех сложенных повариантных данных должна быть равна сумме всех сложенных наблюдений по повторениям, то есть
при этом сумма всех сложенных повариантных данных должна быть равна сумме всех сложенных наблюдений по повторениям, то есть
 =
=  .
.
2. Возведём все наблюдения в квадрат и запишем в соответствующие ячейки.
3. Определим суммы квадратов наблюдений по опыту, а также суммы квадратов сложенных наблюдений по вариантам и повторениям. Вычисляют таким образом:
 = 6,30+5,48+6,76+5,52+8,70……+9,92+9,30 = 163,81
= 6,30+5,48+6,76+5,52+8,70……+9,92+9,30 = 163,81
 = 9,802 + 11,482 + 10,972 + 12,492 + 12,242 = 653,99
= 9,802 + 11,482 + 10,972 + 12,492 + 12,242 = 653,99
 = 14,312 + 14,152 + 14,672 + 13,852 = 812,03
= 14,312 + 14,152 + 14,672 + 13,852 = 812,03
4. Находят суммы квадратов отклонений по формулам таблицы 10:
а) общей дисперсии SSY
SSY =  ;
;
б) дисперсии вариантов SSV
Таблица 11
| Вариант | Урожайность по повторениям (х) | 
| Средний урожай,

| Квадрат урожайностей по повторениям (х2) | ||||||
| I | II | III | IV | I | II | III | IV | |||
| 1. Контроль (без удобрений) | 2,51 | 2,34 | 2,60 | 2,35 | 9,80 | 2,45 | 6,30 | 5,48 | 6,76 | 5,52 |
| 2. N60 | 2,95 | 2,72 | 2,97 | 2,84 | 11,48 | 2,87 | 8,70 | 7,40 | 8,82 | 8,07 |
| 3. Р60 | 2,80 | 2,60 | 2,83 | 2,74 | 10,97 | 2,74 | 7,84 | 6,76 | 8,01 | 7,51 |
| 4. N60P60 | 3,05 | 3,45 | 3,12 | 2,87 | 12,49 | 3,12 | 9,30 | 11,90 | 9,73 | 8,24 |
| 5. N60P60K60 | 3,00 | 3,04 | 3,15 | 3,05 | 12,24 | 3,06 | 9,00 | 9,24 | 9,92 | 9,30 |

| 14,31 | 14,15 | 14,67 | 13,85 | 56,98 | |||||
 = 56,98; = 56,98;  = 2,85; = 2,85;  = 163,81 = 163,81
|
Подготовка данных к дисперсионному анализу однофакторного опыта с ячменём
SSV =  = (653,99 –
= (653,99 –  ): 4 = 1,161;
): 4 = 1,161;
в) дисперсии повторений SSP
SSP =  = (812,03 –
= (812,03 –  ): 5 = 0,070.
): 5 = 0,070.
Таким образом, мы разложили общую дисперсию наблюдений SSY на дисперсию вариантов SSv и дисперсию повторений SSv.
Однако не вся дисперсия у нас была разложена, часть её осталась – это и есть остаточная дисперсия (случайная ошибка). Её обязательно необходимо учитывать по сумме оставшихся квадратов отклонений:
SSZ = SSY –(SSV+ SSP)= 1,469 – (1,161 + 0,070) = 0,238.
5. Следующим этапом обработки является составление таблицы дисперсионного анализа (таблица 12), при помощи которой выявляется «остаточное» рассеяние, характеризующее ошибку опыта.
Таблица 12
Таблица дисперсионного анализа однофакторного полевого опыта
| Дисперсия | Сумма квадратов отклонений, SS | Число степеней свободы, df | Дисперсия,

| Критерий Фишера, F | ||
| фактическое | табличное | |||||
| Общая Вариантов Повторений | 1,469 1,161 0,070 | 0,077 0,290 0,023 | 14,5 | 3,3 | 5,4 | |
| Остаточная | 0,238 | 0,020 |
В эту таблицу вписывают вычисленные суммы квадратов и числа степеней свободы для каждого источника варьирования. Расчёт дисперсии  соответствующего источника варьирования получают делением суммы квадратов на число степеней свободы.
соответствующего источника варьирования получают делением суммы квадратов на число степеней свободы.
Однако не все дисперсии (а их можно вычислить четыре для каждого источника варьирования) представляют интерес для оценки результатов опыта. Наиболее важными из них являются две дисперсии: вариантов и остаточная. Первая из них характеризует варьирование урожайности изучаемых в опыте вариантов (в данном случае удобрений), вторая – случайное варьирование поделяночных урожаев.
Если допустить, что между вариантами нет существенных различий («нулевая гипотеза»), то их дисперсия определяется влиянием случайных причин, например, неравномерностью плодородия по повторениям и по вариантам, также как и дисперсия ошибок. Следовательно, задача сводится к проверке «нулевой гипотезы» о равенстве средних квадратов вариантов и остаточного (ошибки).
Равенство дисперсий проверяют при помощи критерия F, ввёдённого в статистику английским учёным Р.Фишером. Этот показатель представляет собой отношение дисперсий, то есть
 или в нашем случае
или в нашем случае  (43).
(43).
Так как во всех случаях числителем служит большая из сравниваемых дисперсий, то критерий F равен единице или больше неё. Вполне понятно, что чем больше величина критерия F, тем больше вероятность отвержения «нулевой гипотезы».
Фактическое значение F сравнивается с табличным при данном для каждой дисперсии числе степеней свободы df и избранном уровне значимости. Таблицы критерия F (см. приложение 3) представляют собой распределение отношений 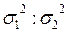 в бесконечном количестве случайных выборок из генеральной совокупности.
в бесконечном количестве случайных выборок из генеральной совокупности.
Если будет доказано равенство дисперсий вариантов и остаточной, то нулевая гипотеза не опровергается, а различия между средними нельзя признать существенными. И наоборот, значимое различие между фактическим и табличным отношением F свидетельствует о наличии существенных различий между средними. Иными словами, если при проведении дисперсионного анализа было установлено, что Fфакт.>Fтабл ., то «нулевая гипотеза (Н0) отвергается, что свидетельствует о наличии существенных или достоверных различий между вариантами, которые значительно выше случайных различий. В обратном случае (Fфакт.≤Fтабл .), «нулевая гипотеза» не отвергается, а это свидетельствует об отсутствии достоверных различий между вариантами что свидетельствует, либо о большом значении ошибки опыта, либо об отсутствии эффективности изучаемого явления. Случай, когда Fфакт. ≤ Fтабл ., свидетельствует о том, что наблюдаемые в опыте различия между выборочными средними не выходят за пределы случайных колебаний урожайности отдельных делянок опыта, или, как часто говорят, находятся в пределах ошибки опыта.
Вычисление фактического отношения дисперсий в рассматриваемом примере с изучением влияния различных минеральных удобрений на урожайность ячменя (таблица 12) даёт Fфакт. = 0,290: 0,020 = 14,5. Обращаясь к таблице (приложение 3), находим на пересечении строки 12 (соответствующей числу степеней свободы меньшей остаточной дисперсии) и графы 4 (для большей дисперсии вариантов) F05 = 3,3 и F01 = 5,4. Так как фактическое значение критерия F больше табличного, следует вывод о том, что между вариантами имеются существенные различия не только при 5%-ном, но и при 1%-ном уровне значимости. То есть эффективность применения минеральных удобрений под ячмень в приведённых дозах доказана.
Несмотря на то, что оценка дисперсий с помощью критерия F позволила выяснить наличие между изучаемыми в опыте вариантами существенные отличия вообще, вопрос об эффективности каждого конкретного вида удобрений и их сочетаний остаётся открытым. Для решения его необходимо определить величину ошибки разности средних. Исходными данными для этого являются определённая величина остаточной дисперсии  и число повторений опыта np.
и число повторений опыта np.
По этим данным вычисляются абсолютная и относительная ошибка средних ( и
и 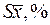 ) по формулам 20 и 21. Следует помнить, что стандартное отклонение
) по формулам 20 и 21. Следует помнить, что стандартное отклонение  , характеризующая в данном конкретном случае среднюю квадратическую ошибку поделяночного урожая, определяется как корень из остаточной дисперсии. Таким образом, получаем:
, характеризующая в данном конкретном случае среднюю квадратическую ошибку поделяночного урожая, определяется как корень из остаточной дисперсии. Таким образом, получаем:
 ,
,

Это означает, что мы можем утверждать, что средняя поделяночная урожайность в нашем опыте варьирует на 0,07 т/га, т.е. урожайность на контрольном варианте без внесения удобрений составляет 2,45±0,07, на варианте N60 – 2,87±0,07 и так далее.
Оценка конкретных различий между средними осуществляется с помощью критерия t, фактическое значение которого представляет собой отношение разности средних d (среднее изменение урожайности или другого наблюдения под действием изучаемых факторов) к ошибки разности 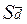 , которая рассчитывается, как и во всех ранее рассмотренных методах статистической обработки по формуле:
, которая рассчитывается, как и во всех ранее рассмотренных методах статистической обработки по формуле:
 или
или 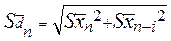 при сравнении с первым контрольным или любым другим вариантом.
при сравнении с первым контрольным или любым другим вариантом.
Поскольку в дисперсионном анализе вместо индивидуальных значений ошибок средних  ,
,  , ….,
, ….,  вычисляют, как и в обобщённом методе (см. раздел 2.3), среднюю ошибку разности
вычисляют, как и в обобщённом методе (см. раздел 2.3), среднюю ошибку разности  рассчитывают по формуле:
рассчитывают по формуле:

В рассматриваемом примере, средняя ошибка разности будет равна:
 , а фактический критерий Стьюдента t для варианта N60:
, а фактический критерий Стьюдента t для варианта N60:
 .
.
Полученное значение  сопоставляют с табличным значением его при числе степеней свободы остаточной дисперсии, в данном случае равном 12 (
сопоставляют с табличным значением его при числе степеней свободы остаточной дисперсии, в данном случае равном 12 ( , а
, а  ). Таким образом, можно с вероятностью в 99% (поскольку
). Таким образом, можно с вероятностью в 99% (поскольку  ≥
≥  ) судить о том, что азотные удобрения в дозе 60 кг/га оказывают положительное влияние на урожайность ячменя.
) судить о том, что азотные удобрения в дозе 60 кг/га оказывают положительное влияние на урожайность ячменя.
Аналогично можно сопоставить все остальные варианты, однако более целесообразным является другой способ, основанный на вычислении критерия существенности НСР при вероятности в 95 или 99%. С эти критерием мы уже встречались при рассмотрении обобщённого метода:
 .
.
Величина НСР (наименьшая средняя разность) при определённом уровне вероятности (95 или 99%-ном) показывает наименьшее значение разности, которое не выходит за пределы ошибки опыта. Таким образом, эффективность рассматриваемого приёма будет только в том случае доказуема, если d ≥ ± НСР.
Для нашего случая величина НСР при 95%-ной вероятности составит:
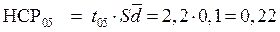 т/га.
т/га.
То есть, если в опыте полученные разности между средними (прибавка или снижение урожая и др.) будут выше или равны 2,2, только в этом случае мы можем утверждать, что это изменение доказано с вероятностью в 95% или, что в 19 случаях из 20 будет действительно отмечаться эффективность от изучаемого приёма.
При 99%-ной вероятности величина НСР будет выше:
 т/га.
т/га.
Значит наименьшее значение разности, с помощью которой можно утверждать об эффективности изучаемого приёма при высоком уровне вероятности 99% (99 случаев из 100) составляет 0,31 т/га.
После окончания статистической обработки с помощью дисперсионного анализа, полученные результаты заносят в таблицу 13.
Таблица13
| Вариант | Урожайность, т/га, х | Прибавка (снижение) урожайности к контролю, d | |
| 1. Контроль (без удобрений) | 2,45 | – | – |
| 2. N60 | 2,87 | +0,42 | +17,1% |
| 3. Р60 | 2,74 | +0,29 | +11,8% |
| 4. N60P60 | 3,12 | +0,67 | +27,3% |
| 5. N60P60K60 | 3,06 | +0,61 | +24,9% |
| НСР05 | 0,22 | ||
| НСР01 | 0,31 |
На основании полученных результатов можно судить об эффективности минеральных удобрений в установленных дозах на урожайность ячменя. Более высокой эффективностью от внесения под ячмень обладают азотные удобрения, поскольку об их эффективности можно судить с 99%-ным уровнем вероятности, в то время как о положительном влиянии варианта Р60 можно утверждать лишь с вероятностью в 95%. Можно отметить, положительное влияние на урожайность ячменя совместного применения азотных и фосфорных удобрений в дозе 60 кг/га, поскольку во всех случаях доказана преимущество этого сочетания по сравнению с раздельным внесением. В то же время добавление к этому сочетанию калийного удобрения в дозе 60 кг д.в./га, было неэффективным.






