1. Проводник с током 2 А имеет форму двух полуокружностей радиусами 9 и 20 см, соединенных между собой прямолинейными проводниками и имеющих общий центр. Определить максимальное значение магнитной индукции в центре полуокружности. (Ответ: 1.012 × 10–5 Тл.)
2. Проводник с током 68 А имеет форму равностороннего треугольника, одна из сторон которого заменена дугой окружности, описанной вокруг треугольника. Найти напряженность магнитного поля в центре этой окружности, если сторона треугольника равна 13 см. (Ответ: 650 А/м.)
3. Бесконечно длинный прямой проводник имеет изгиб в виде перекрещивающейся петли радиусом 33 см. Найти ток, текущий в проводнике, если напряженность магнитного поля в центре петли равна 20 А/м. (Ответ: 10 А.)
4. В центре медного кольца с сечением провода 10 мм2, по которому течет ток 5 А, создается магнитное поле с напряженностью 27 А/м. Найти разность потенциалов, к которой подключено это кольцо. (Ответ: 4.944 × 10–3 В.)
5. Электрон вращается по орбите радиусом 105 пм. Определить скорость электрона, если в центре орбиты им создается магнитное поле с индукцией 12 Тл. (Ответ: 8.269 × 106 м/с.)
6. В центре тонкого длинного соленоида расположена маленькая плоская рамка, состоящая из 26 витков площадью 6 см2 каждый. Плотность навивки соленоида 57 витков на сантиметр, сила тока в соленоиде 2 А. Определить потокосцепление рамки, если ее плоскость перпендикулярна оси соленоида. (Ответ: 2.234 × 10–4 Тл × м2.)
7. Медный проводник с током и поперечным сечением 1 мм2 изогнут в виде трех сторон квадрата и прикреплен концами к непроводящей горизонтальной оси, вокруг которой он может вращаться без трения. При наложении вертикального однородного магнитного поля совершается работа 123 мкДж по отклонению рамки на 60°. Найти сторону рамки. (Ответ: 2.218 × 10–2 м.)
8. Короткая катушка, имеющая поперечное сечение 178 см2 и содержащая 117 витков провода, помещена в однородное магнитное поле, напряженность которого равна 1 А/м. Найти максимальный момент сил, действующий на катушку, когда по ней течет ток силой 526 А. Действием магнитного поля Земли пренебречь. (Ответ: 1.37 × 10–3 Н × м.)
9. Виток диаметром 13 см может вращаться вокруг оси, совпадающей с одним из диаметров витка. Виток установили так, что ось вращения перпендикулярна вектору индукции горизонтальной составляющей магнитного поля Земли, и пустили по нему ток силой 10 А. Найти величину момента сил,
необходимую для удержания его в начальном положении, если В = 20 мкТл. (Ответ: 2.653 × 10–6 Н × м.)
10. Два иона, имеющие одинаковые заряды и прошедшие одинаковую ускоряющую разность потенциалов, влетели в однородное магнитное поле под прямым углом. Первый ион начал вращаться по окружности радиусом 14 см, а второй – 2 см. Определить отношение масс ионов m1/m2. (Ответ: 49.)
11. Катушка, намотанная на немагнитный цилиндрический каркас, имеет 500 витков и индуктивность 10 мГн. Чтобы увеличить индуктивность катушки до 35 мГн, обмотку с катушки сняли и заменили обмоткой из более тонкой проволоки с таким расчетом, чтобы катушка осталась той же длины. Определить число витков после перемотки. (Ответ: 935.)
12. В однородном магнитном поле (В = 1 Тл) по двум шинам, расположенным на расстоянии 66 см под углом 30° к горизонту, равномерно без трения скользит проводник массой 180 г. Вверху шины замкнуты на сопротивление 2 Ом, которое много больше сопротивления остальной цепи. Найти скорость скольжения. (Ответ: 4.05 м/с.)
13. При каком значении напряженности магнитного поля в вакууме объемная плотность энергии этого поля будет такой же, как у электростатического поля с напряженностью 127 МВ/м (тоже в вакууме)? (Ответ:
3.371 × 105 А/м.)
14. В однородном магнитном поле с напряженностью 75 кВ/м в плоскости, перпендикулярной линиям поля, вращается стержень длиной 47 см. Ось вращения проходит через точку, отстоящую от конца стержня на 1/3 его длины. Определить разность потенциалов на концах стержня при частоте вращения 22 с–1. (Ответ: 0.480 В.)
15. Тонкий медный провод массой 3 г согнут в виде квадрата и концы его замкнуты. Квадрат помещен в однородное магнитное поле с индукцией 74982 мкТл, и его плоскость перпендикулярна линиям поля. Какой заряд протечет через проводник, если квадрат, потянув за противоположные вершины, вытянуть в линию? Удельное сопротивление меди 1.6 × 10–8 Ом × м, плотность 8.9 × 103 кг/м3. (Ответ: 9.875 × 10–2 Кл.)
16. Колебательный контур радиоприемника состоит из катушки с индуктивностью 1 мГн и переменного конденсатора, емкость которого может меняться в пределах от 9.7 до 92 пФ. В каком диапазоне длин волн может принимать радиостанции этот приемник? (Ответ: от 186 до 570 м.)
17. Активное сопротивление колебательного контура равно 0,33 Ом. Какую мощность потребляет контур при поддержании в нем незатухающих колебаний с амплитудой силы тока, равной 30 мА? (Ответ: 1.5 × 10–4 Вт.)
18. Какой должна быть добротность контура, чтобы частота, при которой наступает резонанс токов, отличалась от частоты, при которой наступает резонанс напряжений, не более чем на 1 %? (Ответ: Q ≥ 50.)
19. Замкнутый контур в виде рамки площадью 60 см2 равномерно вращается в однородном магнитном поле с индукцией 2 × 10–2 Тл, делая в секунду 20 оборотов. Ось вращения и направление поля взаимно перпендикулярны. Определить амплитудное и действующее значение ЭДС в контуре. (Ответ: 1.51 × 10–2 В; 1.07 × 10–2 В.)
20. Переменное напряжение, действующее значение которого 220 В, частота 50 Гц, подано на катушку без сердечника с индуктивностью
3.18 × 10–2 Гн и активным сопротивлением 10 Ом. Найти количество тепла, выделяющееся в катушке за секунду. (Ответ: 2.4 × 103 Дж/с.)
Контрольная работа № 4
Студент-заочник должен решить восемь задач того варианта, номер которого совпадает с последней цифрой шифра его зачетной книжки (см. табл. 4).
Таблица 4
| Номер варианта | Номер задачи | |||||||
401. Проводник с током 1 А имеет форму полуокружности, замкнутой прямолинейным проводом длиной 10 см. Определить напряженность магнитного поля в центре полуокружности.
402. По двум бесконечно длинным прямым проводникам, пересекающимся под прямым углом и расположенным в одной плоскости, текут токи 11 и 29 А. Определить максимальное значение магнитной индукции в точке, расположенной на пересечении перпендикуляров к проводникам. Расстояние от точки до каждого проводника одинаково и равно 32 см.
403. По двум бесконечно длинным прямым проводникам, пересекающимся под прямым углом и лежащим в одной плоскости, текут токи 30 и 60 А. Определить минимальное значение магнитной индукции в точке, расположенной на пересечении перпендикуляров к проводникам. Расстояние от точки до каждого проводника одинаково и равно 42 см.
404. По двум бесконечно длинным параллельным проводникам, лежащим в одной плоскости, текут противоположно направленные токи 35 и 26 А. Найти напряженность магнитного поля посередине между проводниками, если расстояние между ними равно 37 см.
405. По тонкому проводу, изогнутому в виде прямоугольника, течет ток 88 А. Длины сторон прямоугольника равны 30 и 31 см. Определить напряженность магнитного поля в точке пересечения диагоналей.
406. Бесконечно длинный проводник с током 99 А изогнут под прямым углом. Найти напряженность магнитного поля на биссектрисе прямого угла на расстоянии 83 см от вершины угла.
407. Бесконечно длинный проводник с током 94 А изогнут под прямым углом. Найти магнитную индукцию в точке, лежащей на одном из прямолинейных участков проводника на расстоянии 38 см от вершины угла.
408. Круговой виток радиусом 19 см с током 9 А расположен в плоскости, параллельной бесконечно длинному проводнику с током 5 А, расположенной от проводника на расстоянии 45 см. Найти напряженность магнитного поля в центре витка, если проводник и диаметр витка лежат в одной плоскости, перпендикулярной плоскости витка.
409. Два круговых витка радиусами 31 и 51 см с токами 93 и 4 А лежат в параллельных плоскостях на расстоянии 29 см. Найти напряженность магнитного поля в центре первого витка, если их центры лежат на одном перпендикуляре, а токи направлены в противоположные стороны.
410. По двум бесконечно длинным параллельным проводникам, расположенным на расстоянии 61 см друг от друга, текут противоположно направленные одинаковые токи 62 А. Найти напряженность магнитного поля в точке, расположенной от каждого из проводников на таком же расстоянии, что и расстояние между проводниками.
411. Из медного провода длиной 84 см сделана квадратная рамка. Во сколько раз изменится напряженность магнитного поля в центре квадратной рамки, если длину проводника взять равной 31 см? Разность потенциалов на концах проводника постоянна.
412. Два круговых витка с одинаковыми токами 27 А, имеющие общий центр, расположены во взаимно перпендикулярных плоскостях. Найти напряженность магнитного поля в центре витков, если радиусы их равны 41 и 26 см.
413. Проводник с током 30 А имеет форму квадрата со стороной 31 см. Найти напряженность магнитного поля в одной из его вершин.
414. Горизонтальная составляющая напряженности магнитного поля Земли равна 2 А/м. Какой ток надо пропустить по кольцу радиусом 1 см, чтобы на его оси на расстоянии от центра 40 см создалось такое же магнитное поле?
415. Проводник с током 62 А имеет форму равностороннего треугольника. Определить сторону треугольника, если напряженность магнитного поля в одной из его вершин равна 18 А/м.
416. На расстоянии 133 нм от траектории прямолинейно движущегося электрона максимальное значение магнитной индукции равно 594 нТл. Определить скорость электрона.
417. По кольцу радиусом 99 см течет ток 4 А. Плоскость кольца по диаметру изогнута под прямым углом. Определить величину магнитной индукции в центре кольца.
418. По двум бесконечно длинным параллельным проводникам, лежащим в одной плоскости на расстоянии 1 см друг от друга, текут одинаково направленные токи 95 и 26 А. Найти величину магнитной индукции посередине между ними.
419. По двум окружностям одинакового радиуса, лежащим в перпендикулярных плоскостях и имеющим общий центр, текут одинаковые токи 14 А. Найти радиус окружностей, если напряженность магнитного поля в их центре равна 95 А/м.
420. По двум окружностям одинакового радиуса, лежащим в вертикальной и горизонтальной плоскостях, и имеющим общий центр, текут токи 12 и 59 А. Найти угол между направлением результирующего вектора магнитной индукции в центре окружностей и плоскостью вертикального витка с током.
421. В однородное магнитное поле, индукция которого равна 100 мТл, помещена катушка из 51 витка. Ось катушки параллельна линиям индукции магнитного поля, а радиус ее поперечного сечения равен 1 см. Определить потокосцепление катушки.
422. Определить потокосцепление катушки с током 1 А, которая намотана с плотностью 23 витка/см. Диаметр поперечного сечения катушки 1 см, а длина 32 см.
423. Поток магнитной индукции сквозь один виток тонкого соленоида равен 71 мкВб. Длина соленоида 35 см. Найти магнитный момент соленоида, если его витки плотно прилегают друг к другу. Соленоид считать бесконечным.
424. Квадратный контур со стороной 7 см помещен в однородное магнитное поле так, что угол между его плоскостью и линиями индукции равен 60°. Найти поток, пронизывающий контур, если на него со стороны магнитного поля действует момент сил 81 Н × см. Сила тока в контуре равна 14 А.
425. Виток, по которому течет ток силой 47 А, свободно установился в однородном магнитном поле, индукция которого равна 394 мТл. Диаметр витка 20 см. Какую работу надо совершить, чтобы переместить виток в область пространства без магнитного поля?
426. В однородное магнитное поле, индукция которого равна 58 мТл, помещена квадратная рамка со стороной 8 см, состоящая из 42 витков. Плоскость рамки составляет с направлением магнитного поля угол 30°. Какая будет совершена работа при повороте рамки в устойчивое равновесное положение, если по ней пропустить ток силой 19 А?
427. Рамка гальванометра, состоящая из 224 витков тонкого провода, подвешена на упругой нити в однородном магнитном поле, индукция которого равна 232 мТл. Плоскость рамки параллельна направлению напряженности поля, а ее площадь равна 2 см2. При пропускании через рамку тока 6 мкА она повернулась на 30°. Какая при этом была совершена работа?
428. В однородном магнитном поле, индукция которого равна 457 мТл, проводник переместился перпендикулярно линиям магнитного поля на 37 см. При этом была совершена работа, равная 54 мДж. Чему равна сила тока в проводнике, если его длина равна 45 см?
429. Два длинных параллельных проводника с токами 34 и 32 А расположены на расстоянии 15 см друг от друга. Токи в проводниках текут в одном направлении. Какую по величине работу нужно совершить на каждый метр длины проводника, чтобы раздвинуть их до расстояния 31 см?
430. Плоский квадратный контур со стороной 10 см свободно установился в однородном магнитном поле, индукция которого равна 0.4 Тл. При повороте контура внешними силами вокруг оси, проходящей через середины противоположных сторон, на угол 60° была совершена работа 2 мДж. Определить силу тока, текущего в контуре. Ток при повороте не изменяется.
431. В одной плоскости расположены длинный прямой проводник с током 11 А и квадратная рамка со стороной 8 см и током 5 А. Ось, проходящая через середины противоположных сторон, параллельна проводнику и удалена от него на 24 см. Определить максимальную по величине работу по перемещению рамки в аналогичное положение с другой стороны проводника.
432. В однородное магнитное поле, индукция которого равна 50 мТл, помещен длинный прямой проводник с током так, что на каждый метр его длины действует максимальная сила 7 Н/м. Найти силу тока в проводнике.
433. В однородное магнитное поле, индукция которого равна 59 мТл, помещен прямой проводник с током 7 А так, что угол между направлением тока и вектором магнитной индукции составляет 30°. Определить длину проводника (подводящие ток провода находятся вне поля). На проводник со стороны магнитного поля действует сила 15 мН.
434. Рамка гальванометра длиной 4 см и шириной 2 см, содержащая 109 витков тонкой проволоки, находится в однородном магнитном поле, индукция которого равна 575 мТл. Плоскость рамки параллельна направлению магнитного поля. Найти момент сил, действующий на рамку со стороны магнитного поля, когда по ней пропускают ток силой 8 мА.
435. Между полюсами электромагнита создается однородное магнитное поле. В поле помещен проводник с током так, что на него действует максимальная сила. На какой угол (в радианах) надо повернуть проводник, не меняя ток, чтобы уменьшить силу в 12 раз?
436. Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые по величине токи 89 А каждый. Определить силу, действующую на рамку, если ближайшая к проводу сторона рамки находится от него на расстоянии, равном периметру рамки.
437. На проволочный виток радиусом 13 см, помещенный в однородное магнитное поле, действует максимальный момент сил 497 мкН × м. Сила тока в витке равна 9 А. Определить магнитную индукцию поля. Действием магнитного поля Земли пренебречь.
438. По двум параллельным прямым проводникам одинаковой длины по 9 м, находящимся на расстоянии 15 см друг от друга, текут одинаковые по величине токи – 1113 А каждый. Вычислить максимальную силу взаимодействия этих токов.
439. Электрон движется в однородном магнитном поле с индукцией 0.1Тл по окружности. Определить угловую скорость вращения электрона.
440. Протон, прошедший разность потенциалов 1731 В, влетел в однородное магнитное поле с напряженностью 423 кА/м и начал двигаться по окружности. Вычислить ее радиус.
441. Контур в виде полуокружности радиусом 4 см, являющийся частью замкнутой цепи с сопротивлением 36 Ом, вращают вокруг его диаметра с угловой скоростью 17 рад/с в однородном магнитном поле с индукцией 2646 мкТл. Найти максимальную мощность, выделяющуюся в цепи. Линии поля перпендикулярны оси вращения. Полем тока индукции пренебречь.
442. В однородное магнитное поле помещена катушка, имеющая 65 витков, площадь сечения 6 мм2, а ее ось параллельна линиям поля. При повороте катушки на 180° вокруг диаметра по ее обмотке протекает заряд 6 мкКл (сопротивление цепи 78 Ом). Определить индукцию магнитного поля.
443. Электрон в бетатроне движется по орбите радиусом 41 см и приобретает за один оборот кинетическую энергию 15 эВ. Вычислить скорость изменения магнитной индукции < В >, считая ее постоянной в течение периода. < В > – среднее значение магнитной индукции в пределах круга, очерченного орбитой электрона.
444. Сколько метров тонкого провода надо взять для изготовления соленоида длиной 79 см с индуктивностью 8108 мкГн, если диаметр сечения соленоида много меньше его длины?
445. Найти индуктивность соленоида длиной 67 см, обмоткой которого является медная проволока массы 6 кг. Сопротивление обмотки 23 Ом. Диаметр сечения соленоида много меньше его длины. Для меди удельное сопротивление равно 0.016 мкОм × м, плотность 8900 кг/м 3.
446. Магнитный поток 84 мВб пронизывает замкнутый контур. Определить среднее значение ЭДС. индукции, возникающей в контуре, если магнитный поток изменится до нуля за время 7 мс.
447. Прямой провод длиной 23 см движется в однородном магнитном поле с постоянной скоростью 1 м/с перпендикулярно линиям индукции. Разность потенциалов между концами провода равна 8 мВ. Найти индукцию магнитного поля.
448. Рамка площадью 232 см2 равномерно вращается с частотой 12 Гц относительно оси, которая лежит в плоскости рамки и перпендикулярна линиям однородного магнитного поля с индукцией 1654 мкТл. Найти среднее значение ЭДС индукции за время, в течение которого магнитный поток, пронизывающий рамку, изменится от нуля до максимального значения.
449. В однородном магнитном поле с индукцией 8240 мкТл равномерно с частотой 377 мин–1 вращается рамка, которая содержит 108 витков и имеет площадь 80 см2. Ось вращения лежит в плоскости рамки и перпендикулярна линиям поля. Найти максимальную величину ЭДС индукции, возникающей в рамке.
450. Короткая катушка, имеющая 321 виток, вращается с угловой скоростью 6 рад/с в однородном магнитном поле (В = 3065 мкТл) вокруг оси, совпадающей с ее диаметром и перпендикулярной линиям поля. Найти значение ЭДС индукции для момента времени, когда плоскость поперечного сечения (s = 79 см2) катушки составляет угол 60° с линиями поля.
451. Катушка из 417 витков, площадью 80 см2 каждый, присоединена к прибору для измерения заряда. Катушка помещена в однородное магнитное поле с индукцией 2163 мкТл так, что линии индукции магнитного поля перпендикулярны площади витков. Определить величину заряда, протекающего через прибор при перемещении катушки в пространство без поля. Сопротивление цепи 22 Ом.
452. Магнитное поле внутри длинного соленоида однородно и его индукция с течением времени изменяется по закону косинуса с частотой 30 Гц. Радиус соленоида 3 см, число витков 521. Определить максимальное значение индукции магнитного поля, если максимальное напряжение, возникающее на обмотке соленоида, равно 89 В.
453. В однородное магнитное поле помещена катушка, обмотка которой имеет сопротивление 126 Ом, число витков 263 и площадь сечения 7 см2. Ось катушки параллельна линиям поля. В течение некоторого времени индукция магнитного поля уменьшилась от 680 до 102 мТл. Найти заряд, возникающий в катушке. Катушку считать короткой.
454. Катушка состоит из 330 витков и по ее обмотке течет ток силой 1 А. Возникающий при этом магнитный поток равен 17 мВб. Найти энергию магнитного поля внутри катушки.
455. В однородное магнитное поле с индукцией 5 Тл помещен плоский виток, имеющий сопротивление 6 Ом, площадь 9 см2, а его плоскость перпендикулярна линиям поля. Сам виток замкнут на гальванометр. При повороте витка через прибор прошел заряд 90 мкКл. На какой угол повернули виток?
456. В одной плоскости лежат длинный прямой проводник с током и плоская прямоугольная рамка со сторонами 2 и 7 см, содержащая 746 витков Расстояние от прямого проводника до ближайшей к нему (большей) стороны рамки 4 см. Определить взаимную индуктивность проводника и рамки.
457. В однородном магнитном поле с индукцией 1229 мкТл вращается с постоянной угловой скоростью 54 рад/с квадратная рамка со стороной 2 см. Ось вращения перпендикулярна линиям индукции и совпадает с одной из сторон квадрата. Определить максимальное значение ЭДС индукции, возникающей в рамке.
458. На картонный каркас круглого сечения виток к витку намотан в один слой провод, толщина которого равна 765 мкм. Найти плотность энергии магнитного поля внутри катушки при силе тока в обмотке 602 мА. Поле внутри катушки считать однородным.
459. На деревянном цилиндре имеется обмотка из медной проволоки, масса которой 77 г. Расстояние между крайними витками много больше диаметра цилиндра и равно 79 см. Сопротивление обмотки 24 Ом. Найти энергию магнитного поля на оси цилиндра, если по обмотке течет ток 4 А. Удельное сопротивление меди равно 0.016 мкОм × м и плотность меди 8900 кг/м3.
460. Соленоид содержит 2468 витков, а сила тока в его обмотке равна 2 А. Найти энергию магнитного поля внутри соленоида, полагая его бесконечно длинным. Магнитный поток через поперечное сечение соленоида равен 314 мкВб.
461. Контур состоит из катушки с индуктивностью 83.4 мкГн и сопротивлением 1 Ом и конденсатора емкостью 23.2 нФ. Какую мощность должен потреблять контур, чтобы в нем поддерживались незатухающие колебания, при которых максимальное напряжение на конденсаторе равно 0.981 В?
462. Контур с индуктивностью 33.4 мГн, сопротивлением 20.73 Ом и некоторой емкостью возбуждается короткими электрическими импульсами. С какой максимальной частотой их можно подавать, чтобы возникающие колебания не накладывались друг на друга? (Колебания не накладываются, если их амплитуда за период между импульсами уменьшается не менее чем в 10 раз.)
463. Контур состоит из катушки с индуктивностью 2.05 × 10–2 Гн и сопротивлением 8 Ом и конденсатора емкостью 6.59 нФ. Найти логарифмический декремент затухания колебаний в контуре.
464. Во сколько раз уменьшится разность потенциалов на обкладках конденсатора за один период колебаний в контуре, если индуктивность контура 40 мкГн, емкость 180 пФ и сопротивление 60 Ом?
465. Какую мощность потребляет контур с активным сопротивлением 603 Ом при поддержании в нем незатухающих колебаний с амплитудой тока 854 мА?
466. Определите добротность Q колебательного контура, состоящего из катушки индуктивностью L = 2мГн, конденсатора ёмкостью C = 0.2 мкФ и резистора сопротивлением R = 80 Ом.
467. Какая часть запасенной энергии сохранится в контуре через 0.560 мс, если контур настроен на частоту 77.3 кГц, а добротность контура равна 89.
468. Индуктивность, емкость и сопротивление колебательного контура равны соответственно 70 Гн, 26 мкФ, 17 Ом. При какой частоте внешней ЭДС амплитудное значение напряжения на конденсаторе максимально? Ответ дать в радианах в секунду.
469. На каком ближайшем расстоянии от источника колебаний с периодом 1 мс через время, равное половине периода после включения источника, смещение точки от положения равновесия по синусоидальному закону равно половине амплитуды? Скорость распространения колебаний равна 331 м/с. Считать, что в момент включения источника все точки находятся в положении равновесия.
470. Емкость и индуктивность колебательного контура равны
С = 61.9 мкФ и L = 0.145 Гн. Через сколько времени после начала зарядки конденсатора его энергия в 31 раз превысит энергию катушки индуктивности? Сопротивлением контура пренебречь.
471. Колебательный контур с емкостью 5.22 нФ настроен на частоту 369 кГц. При колебаниях максимальное напряжение на конденсаторе равно 116 В. Пренебрегая активным сопротивлением контура, определите максимальный ток в контуре.
472. Колебательный контур состоит из конденсатора с емкостью 0.902 мкФ и катушки с индуктивностью 8.23 мГн. На какую длину волны настроен контур? Активным сопротивлением контура пренебречь.
473. Батарея, состоящая из двух последовательно соединенных конденсаторов с емкостью по 0.811 мкФ каждый, разряжается через катушку
(L = 462 мкГн, R = 54 Ом). Возникнут ли при этом колебания?
474. Источник тока замкнули на катушку с сопротивлением 10 Ом и индуктивностью 1 Гн. Через сколько времени сила тока замыкания достигнет 0.9 предельного значения?
475. Колебательный контур состоит из параллельно соединенных конденсатора емкостью 1 мкФ и катушки с индуктивностью 1 мГн. Сопротивление контура очень мало. Определить частоту колебаний.
476. Катушка (без сердечника) длиной 50 см и сечением 3 см2 имеет 1000 витков и соединена параллельно с конденсатором. Конденсатор состоит из двух пластин площадью 75 см2 каждая. Расстояние между пластинами 5 мм, диэлектрик – воздух. Определить период колебаний контура.
477. Колебательный контур имеет индуктивность 1.6 мГн, емкость 0.04 мкФ и максимальное напряжение на зажимах 200 В. Определить максимальную силу тока в контуре. Сопротивление контура очень мало.
478. Колебательный контур состоит из катушки индуктивностью L = 2мГн, конденсатора ёмкостью C = 0.2 мкФ и резистора сопротивлением R = 80 Ом. Определите логарифмический декремент затухания колебаний.
479. Колебательный контур состоит из индуктивности 0.01 Гн, емкости 0.405 мкФ и сопротивления 2 Ом. Найти, во сколько раз уменьшится разность потенциалов на обкладках конденсатора за время одного периода.
480. Какую индуктивность надо включить в колебательный контур, чтобы при емкости 2 мкФ получить звуковую частоту 1000 Гц? Сопротивлением контура пренебречь.
РАЗДЕЛ 5. ОПТИКА
Основные формулы
1. Абсолютный показатель преломления среды
n = c/V,
где с – скорость света в вакууме; V – скорость света в данной среде.
2. Относительный показатель преломления
n21 = n2/n1 = V1/V2,
где n21 – относительный показатель преломления второй среды относительно первой; n1 – абсолютный показатель преломления первой среды; n2 – абсолютный показатель преломления второй среды; V1, V2 – скорости света в первой и во второй средах.
3. Закон преломления света
sin a / sin b = n21,
где a – угол падения луча; b – угол преломления луча.
4. Условие полного отражения света на границе раздела двух сред (при движении луча из оптически более плотной среды в оптически менее плотную среду)
sin a0 = n21,
где a0 – предельный угол полного внутреннего отражения; n21 – относительный показатель преломления.
5. Оптическая длина пути луча
L = n l,
где n – показатель преломления среды; l – геометрическая длина пути луча.
6. Оптическая разность хода двух лучей
D = L1 – L2.
7. Оптическая разность фаз
Dφ = 2π (D/λ),
где λ – длина световой волны.
8. Условие максимума при интерференции света
D = 
kl, (k = 0, 1, 2,…),
где D – оптическая разность хода лучей; k – целое число; l – длина световой волны.
9. Условие минимума при интерференции света
D = (2k + 1) l/2, (k = 0, 1, 2,…).
10. Оптическая разность хода лучей, возникающая при отражении монохроматического света от тонкой пленки:
или
,
где d – толщина пленки; n – показатель преломления пленки; a – угол падения света; b – угол преломления света в пленке.
11. Радиус светлых колец Ньютона в отраженном свете
где k – номер кольца (k = 1, 2, 3,…); R – радиус кривизны линзы.
12. Радиус темных колец Ньютона в отраженном свете
13. Условие максимума для дифракции на одной щели
а sin j = (2k+1)l/2, (k = 1, 2, 3,…);
условие минимума для дифракции на одной щели
а sin j = kl, (k = 1, 2, 3,…),
где а – ширина щели; k – порядковый номер максимума или минимума.
14. Условие главного максимума для дифракционной решетки
d sin j = kl, (k = 0, 1, 2,…);
условие главного минимума для дифракционной решетки
a sin j = kl, (k = 1, 2, 3,…),
где j – угол дифракции; k – целое число (порядок спектра); l – длина волны; d – период решетки; d = a + b, где a – ширина прозрачных щелей решетки, b – ширина непрозрачных промежутков между щелями.
15. Условие добавочных минимумов для дифракционной решетки
d sin j = kl/N, (k = 1, 2,…,N-1,N+1,…),
где N– количество щелей.
16. Разрешающая способность дифракционной решетки
R = λ/Δλ = kN,
где Δλ – наименьшая разность длин волн двух соседних спектральных линий (λ и λ + Δλ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N – полное число щелей решетки; k – порядок спектра.
17. Формула Вульфа – Брэгга
2d sin Θ = kλ, (k = 0, 1, 2,…),
где Θ – угол скольжения; d – расстояние между атомными плоскостями кристалла.
18. Формулы Френеля
,
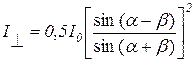где I┴ – интенсивность световых колебаний в отраженном луче, совершающихся в направлении, перпендикулярном к плоскости падения света; I| | – интенсивность световых колебаний в отраженном луче, совершающихся в направлении, параллельном плоскости падения света; I0 – интенсивность падающего естественного света; a – угол падения; b – угол преломления.
19. Закон Брюстера
tg aБ = n21,
где aБ – угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; n21 – относительный показатель преломления второй среды относительно первой.
20. Закон Малюса
I = I0 cos2α,
где I – интенсивность этого света после анализатора; I0 – интенсивность плоскополяризованного света, падающего на анализатор; α – угол между направлением колебаний света, падающего на анализатор, и плоскостью пропускания анализатора.
21. Энергия фотона
Е = hn,
где h – постоянная Планка; n – частота излучения.
22. Импульс фотона
p = hn/c.
23. Масса фотона
m = hn/c2.
24. Релятивистская масса
,
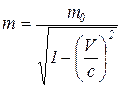где m0 – масса покоя частицы; V – ее скорость; с – скорость света в вакууме.
25. Взаимосвязь массы и энергии релятивистской частицы
где (E0 = m0c2) – энергия покоя частицы.
26. Полная энергия свободной частицы
Е = Е0 + Т,
где Т – кинетическая энергия релятивистской частицы.
27. Кинетическая энергия релятивистской частицы
T = (m – m0) c2.
28. Импульс релятивистской частицы
.
29. Закон Стефана – Больцмана
Rэ= σ T4, 
,
где Rэ – излучательность (энергетическая светимость) абсолютно черного тела; σ – постоянная Стефана – Больцмана; Т – термодинамическая температура.
30. Закон смещения Вина
λmax= b/T,
где λmax – длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела; b – первая константа Вина, b = 2,9 × 10–3 м × К.
31. Второй закон Вина
(rλ)max = C T5,
где (rλ) max – максимальная спектральная плотность энергетической светимости абсолютно черного тела; С – вторая константа Вина,
С = 1,29 × 10–5 Вт/(м3 × К5).
32. Уравнение Эйнштейна для фотоэффекта
hn = Aвых + mV2max/2,
где Авых – работа выхода электрона из фотокатода; mV2max/2 – кинетическая энергия фотоэлектрона.
33. Формула Комптона
Δλ = λ' – λ = h(1 – cos Θ)/(m0c),
где λ – длина волны фотона, встретившегося со свободным электроном; λ' – длина волны фотона, рассеянного на угол Θ после столкновения с электроном; m – масса электрона.
34. Комптоновская длина волны
Λ = h/(m0c) = 2,426 пм.
Примеры решения задач
Пример 1. Для измерения показателей преломления прозрачных веществ используют интерферометр (см. схему). Здесь S – узкая щель, освещаемая монохроматическим светом (λ0 = 0.589 мкм); 1 и 2 – две одинаковые трубки с воздухом, длина каждой из которых l = 10 см; Д – диафрагма с двумя щелями; Л – собирающая линза. Когда воздух в трубке 2 заменили аммиаком, то ранее наблюдавшаяся на экране Э интерференционная картина сместилась вверх на N = 17 полос. Определить показатель преломления ń аммиака, если для воздуха n = 1.00029.
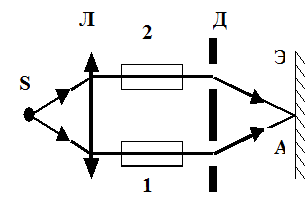Решение. Согласно принципу Гюйгенса, две щели в освещаемой диафрагме можно рассматривать как вторичные источники световых волн. Так как при этом на диафрагму падает свет от одного источника S, то обе щели являются когерентными источниками и на экране возникает интерференционная картина.
Результат интерференции света в какой-либо точке А экрана определяется из соотношения
, (1)
где Δ = L2 – L1 – оптическая разность хода лучей S1A, S2A; k – целое число; λ0 – длина световой волны в вакууме.
Так, для светлых интерференционных полос имеем
(2)
где k – номер данной полосы (отсчет ведется от центральной полосы, для которой k = 0).
Оптическая длина пути, проходимого световым лучом в однородной среде с показателем преломления n,
L = ns, (3)
где s – геометрическая длина пути луча.
Замена воздуха аммиаком в трубке 2 вызвала изменение оптической длины пути L2 светового луча S2A на величину
δ = ńl –nl. (4)
На столько же изменилась величина Δ = L2 – L1. При этом, согласно формуле (1), изменилось условие интерференции света в точке А.
В процессе замены воздуха аммиаком, когда величина Δ непрерывно изменялась, в точке А экрана постепенно сменяли друг друга светлые и темные интерференционные полосы – интерференционная картина перемещалась по экрану. Ее смещению на одну полосу соответствует в формуле (2) изменение числа k на единицу и, следовательно, изменение Δ на величину ±λ0. Значит, при смещении интерференционной картины на N полос оптическая разность хода Δ изменилась на величину ±Nλ0. Но это изменение выражается формулой (4), поэтому
ńl – nl =±Nλ0. (5)
Знак в правой части (5) определяется направлением смещения интерференционной картины на экране. Действительно, рассмотрим центральную интерференционную полосу (k = 0). Когда в обеих трубках был воздух, она располагалась на экране на равных расстояниях от щелей в диафрагме. Перемещение полосы вверх в процессе замены воздуха в трубке 2 аммиаком свидетельствует, как это видно из чертежа, об увеличении оптической длины пути L1 луча S1A. Но для центральной интерференционной полосы, как бы она ни перемещалась по экрану, всегда
Δ = L2 – L1 = ± kλ0 = 0.
Следовательно, оптическая длина пути L2 луча S2A также увеличилась. Очевидно, это могло произойти только вследствие неравенства ń > n. Таким образом, отбросив знак «минус» в правой части (5), получим
ń = n + (N λ0 )/ l = 1.00039.
Пример 2. Для уменьшения потерь света при отражении от стекла на поверхность объектива (n = 1,7) нанесена тонкая прозрачная пленка (n = 1,3). При какой наименьшей толщине ее произойдет максимальное ослабление отраженного света, длина волны которого приходится на среднюю часть видимого спектра (λ = 0,56 мкм)? Считать, что лучи падают нормально к поверхности объектива.
Решение. Свет, падая на объектив, отражается как от передней, так и от задней поверхностей тонкой пленки. Ход лучей для случая их наклонного падения изображен на схеме. Отраженные лучи 1 и 2 интерферируют. Условие минимума интенсивности света при интерференции выражается формулой
где Δ – оптическая разность хода; (m = 2k + 1) – нечетное число (k = 0, 1, 2, 3,…); λ0 – длина световой волны в вакууме, т. е.
(1)
Оптическая разность хода лучей, отраженных от двух поверхностей тонкой пленки, окруженной одинаковыми средами, определяется формулой
(2)
где h – толщина пленки; n – показатель преломления пленки; b – угол преломления. В данном случае пленка окружена различными средами – воздухом (n = 1) и стеклом (n = 1.7). Из неравенства n1<n<n2 следует, что оба луча 1 и 2, отражаясь от границы с оптически более плотной средой, «теряют» полуволну. Так как это не влияет на их разность хода, то в (2) следует отбросить член λ0/2. Кроме того, полагая b = 0, получим
(3)
Из равенств (1) и (3) находим толщину пленки:
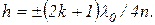
Учитывая, что h – положительная величина и что значению hmin соответствует k = 0, получим
hmin = λ0/4n = 0.11 мкм.
Пример 3. Монохроматический свет с длиной волны λ = 7 × 10–7 м падает нормально на дифракционную решетку с периодом d = 2 × 10–6 м. Длина решетки l = 4 × 10–2 м. Определить угловую ширину дифракционного максимума Δψ первого порядка.
Решение. Между двумя главными максимумами, соответствующими разности хода лучей от соседних щелей d· sin φ= kλ, где k = 0, ± 1, ± 2, …, лежат (N – 1) добавочных минимумов, определяемых разностью хода
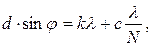
где c может принимать целые значения от 1 до (N – 1).
Угловое расстояние между главными максимумом и соседним минимумом определяется требованием, чтобы разность хода возросла на λ/N, т. е.
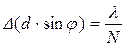
или
,
отсюда
что составляет полуширину максимума.
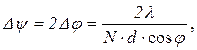
но N = l / d; Δψ – полная ширина максимума. Угол j определим из условия первого максимума на дифракционной решетке:
d·sin φ = λ,
откуда
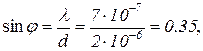
cos φ = 0.935.
Следовательно,
рад.
Пример 4. Экран Р находится на расстоянии 4 м от точечного монохроматического источника света. Посередине между экраном и источником света помещена диафрагма М с круглым отверстием. При каком радиусе отверстия центр дифракционных колец, наблюдаемых на экране Р, будет наиболее темным, если длина волны источника света равна 6 × 10–7 м?
Решение. Проведем из точки А ряд концентрических сфер с радиусами, отличающимися на λ/2, и тем самым разобьем отверстие в диафрагме М на зоны Френеля (см. схему). Зная число зон, уложившихся в отверстии, можно определить освещенность в точке А экрана Р.
Пусть отверстие пропускает m зон Френеля, тогда радиус m -й зоны rm есть одновременно радиус отверстия:
Очевидно, что освещенность центра колец, наблюдаемых на экране Р, минимальна при m = 2, так как в этом случае действие одной половины зон компенсирует действие другой половины.
Подставляя числовые данные, получаем
м.
Пример 5. Определить угол φ между главными плоскостями поляризатора и анализатора, если интенсивность света Ι, прошедшего через эту систему, уменьшилась в восемь раз. Поглощением света пренебречь.
Решение. Интенсивность света, прошедшего через систему «поляризатор – анализатор», меняется по закону Малюса:
I2 = I1·cos2 φ = 0.5·I0·cos2 φ.
Согласно условию задачи,
отсюда
,
φ = 60°.
Из закона Малюса (I2 = I1· cos2 φ) следует, что при повороте осей поляризатора и анализатора на угол φ = 90 ° свет через такую систему проходить не будет (I2 = 0).
Пример 6. Естественный свет падает под углом Брюстера на поверхность стекла (n = 1.6). Определить коэффициент отражения.
Решение. Коэффициент отражения ρ показывает, какую долю от интенсивности падающего света I составляет интенсивность отраженного света I', т. е.
ρ = I'/I. (1)
Свет, отраженный от диэлектрика под углом Брюстера, полностью поляризован. При этом в отраженном луче присутствуют лишь световые колебания, перпендикулярные плоскости падения. Поэтому на основании формулы Френеля
(2)
где I┴ и I'┴ – интенсивности падающего и отраженного света, у которого колебания светового вектора перпендикулярны плоскости падения; a – угол падения; b – угол преломления, и соотношения (aБ + b = π/2) получим
(3)
Так как в естественном свете величина 
составляет половину от полной интенсивности I, то из (1), (3) следует
(4)
Углы aБ и b можно найти, зная показатель преломления стекла n. По закону Брюстера, tg aБ = n =1.6. Отсюда aБ = 58 °, b = 90 ° – 58 ° = 32 °; aБ – b = 26 °.
Теперь из (4) получим
ρ = 0.5 sin2 26° = 0.10 или 10 %.
Пример 7. Красная граница фотоэффекта для цезия равна
λ0 = 6.53 × 10–7 м. Определить скорость фотоэлектронов V при облучении цезия фиолетовыми лучами с длиной волны λ = 5 × 10–7 м (h = 6.625 × 10–34 Дж × с,
с = 3 × 108 м/с, т = 9.11 × 10–31 кг).
Решение. Скорость фотоэлектронов может быть определена из уравнения Эйнштейна для фотоэффекта
.
Работу выхода электрона из цезия можно определить, зная красную границу фотоэффекта, т. е. ту минимальную энергию, при которой еще наблюдается фотоэффект:
.
Определяя из уравнения Эйнштейна скорость электрона, получим
В системе СИ скорость
Пример 8. Исследования спектра излучения Солнца показывают, что максимум спектральной плотности энергетической светимости соответствует длине волны 0.5 мкм.
Принимая Солнце за абсолютно черное тело, определить:
а) энергетическую светимость Солнца;
б) поток энергии, излучаемой Солнцем;
в) энергетическую освещенность поверхности Земли при нормальном падении лучей без учета поглощения в атмосфере.
Решение. а)Энергетическая светимость RЭ абсолютно черного тела выражается формулой Стефана – Больцмана
RЭ = σТ4, (1)
где σ – постоянная Стефана – Больцмана; Т – абсолютная температура излучающей поверхности.
Температура может быть определена из закона смещения Вина
, (2)
где λ0 – длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела; b – постоянная Вина.
Выразив из закона смещения Вина температуру Т и подставив ее в (1), получим
(3)
Выразим величины в системе СИ:
σ = 5.67 × 10–8 Вт/(м2 × К4);
b = 2.9 × 10–3 м × К;
λ0 = 0.5 мкм = 5 × 10–7 м.
Подставив эти числовые значения в (3) и произведя вычисления, получим
RЭ 
Вт/м2.
б)Поток энергии Р, излучаемой Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности:
P = RЭ S,
или
P = 4π r2 RЭ, (4)
где r = 6.96 × 108 м – радиус Солнца.
Подставив эти значения в (4), найдем
Р = 
Вт.
в)Энергетическую освещенность ЕЭ поверхности Земли определим, если разделим поток энергии Р, излучаемой Солнцем, на площадь S' поверхности сферы, радиус которой равен среднему расстоянию от Земли до Солнца:
ЕЭ = Р/ S',
или
ЕЭ = 
(5)
где R = 1.50 × 1011 м – среднее расстояние от Земли до Солнца.
Подставив числовые значения в (5), получим
ЕЭ = 
Вт/м2.
