План:
1. Взаємозв’язки показників податкової діяльності.
2. Непараметричні методи зв’язку показників податкової діяльності.
3. Поняття про кореляційний зв’язок у податковій статистиці.
4. Графічний аналіз зв’язку за допомогою кореляційного поля.
5. Розрахунок параметрів рівняння регресії.
6. Визначення щільності зв’язку між показниками податкової діяльності.
7. Побудова довірчих інтервалів.
8. Множинна і часткова кореляції.
1. Взаємозв’язки показників податкової діяльності. Одним із найважливіших завдань податкової статистики є вивчення взаємозв’язків соціально-економічних явищ, виявлення та вимір причинних залежностей. Практична економічна діяльність та наукові дослідження ставлять безліч конкретних завдань, які можуть бути реалізовані лише аналітичним підходом, використанням широкого спектра методів статистичного аналізу. Так, у ході дослідження взаємозв’язків вирішуються, наприклад, такі завдання, як наявність та оцінка щільності зв'язку між тяжкістю порушення податкового законодавства, способом ухилення від сплати податків та показниками штрафів, видами i розмірами штрафів, впровадженням додаткових та умовних штрафів, характером справ, що розглядаються податковими інспекціями; особливими обставинами скоєного порушення податкового законодавства (наприклад, умовами економічної ситуації) та характером їx врахування податковим органом у ході винесення вироку; рівнем освіти i станом працівників податкових органів та якістю оподаткування; динамікою окремих видів i груп різних порушень; видом, строком покарання, обґрунтування звільнення від сплати податків ociб, що займаються благодійною діяльністю, меценатством, тощо.
Статистичний розподіл характеризується наявністю певного рівня варіації (V) увеличині ознаки окремих одиниць сукупності. Статистика вивчає як фактори, які формують рівень ознаки у досліджуваної сукупності, так i конкретний вплив кожного з них на результативний фактор. Вивчення залежності варіації досліджуваної ознаки від зовнішніх умов становить зміст теорії кореляції. Варіація кожної досліджуваної ознаки перебуває в тісному взаємозв’язку з варіацією інших ознак, що характеризують досліджувані сукупності. Наприклад, варіація показника тяжкості порушення податкового законодавства та спосіб його здійснення залежать від освіти, віку, статі, умов виховання, характеру роботи та інших факторів.
Таким чином, у ході дослідження конкретних залежностей певні ознаки виконують функції факторів, які зумовлюють зміну інших ознак i характеризують причину цих змін. Ці ознаки називаються факторними, а ті, що характеризують наслідки, — результативними. Наприклад, при вивченні зв'язку між рівнем порушення податкового законодавства в регіоні та кількістю населення, факторною ознакою є чисельність населення, а результативною — рівень порушень.
Залежності між явищами i процесами, які виникають у сфері податкової діяльності, можна поділити на два види: функціональні та стохастичні.
Функціональні зв'язки характеризуються повною відповідністю між змінами факторної та результативної ознак. Вони здебільшого зустрічаються в точних науках, де зв'язок може бути виражений конкретною формулою, яка характеризує конкретне явище або процес. Наприклад, у фізиці сила електричного струму (Т) прямо пропорційна напрузі (Н) i обернено пропорційна опору (О), тобто формула матиме такий вигляд:
(9.1)
У даному випадку результативна ознака визначається двома факторами, які мають обернену дію, — сила струму буде тим більшою, чим більша напруга або менший oпip. Таким чином, функціональний динамічний зв'язок точний i повний, діє в мало залежному від зовнішнього впливу середовищі.
Стохастична залежність проявляється у тому, що при зміні факторної ознаки змінюється розподіл одиниць сукупності за результативною ознакою, тобто умовні розподіли при різних значеннях факторної ознаки різні. При цьому не можна передбачити, яке буде значення результативної ознаки у конкретної одиниці сукупності при даному рівні факторної ознаки.
У сфері податкової діяльності однозначні повні i точні зв'язки майже відсутні, оскільки порушення податкового законодавства — це масове явище, на яке впливають багато взаємопов’язаних факторів, зміна кожного з яких може вплинути на характер взаємодії всієї досліджуваної сукупності.
Причинна залежність між факторною i результативною ознаками неоднозначна. Результативна ознака формується під впливом комплексу факторних ознак. Кожному значенню факторної ознаки може відповідати кілька значень результативної. Це свідчить про те, що зв'язок між факторною i результативною ознаками багатозначний i має імовірнісний характер. Багатозначність проявляється в тому, що, з одного боку, те чи інше порушення податкового законодавства формується під впливом багатьох факторів, а з другого — кожен фактор взаємодіє з комплексом інших i може формувати не один, а кілька наслідків, які можуть включати різні види поведінки.
Особливості оподаткування зумовлюють імовірнісний характер багатозначності зв'язку між явищами та процесами податкової дiяльнocтi. Їх сутність полягає в тому, що у разі зміни тiєї чи іншої умови, якщо навіть залишається одна i та сама причина, може змінюватися i результативна ознака. Якщо форма зв'язку визначає залежність результативної ознаки від факторної не однозначно, а лише з певною часткою iмовipностi, вона є неповною i називається кореляційним зв'язком, який проявляється не в кожному конкретному випадку, а в середньому, тобто за наявності великої кількості спостережень.
Взаємозв’язки показників розрізняють:
а) за напрямом — прямі й обернені. У першому випадку зв'язок характеризує зміну результативної ознаки відповідно до зміни факторної. У другому — зростання результативної ознаки при зниженні факторної, i навпаки;
б) за аналітичною формою — прямолінійна та криволінійна залежність. При прямолінійній залежності в ході однакових змін середніх значень факторної ознаки відбуваються однакові зміни середніх значень результативної ознаки. Криволінійна кореляційна залежність характеризує відповідність однаковим значенням середніх значень факторної ознаки нерівні зміни середніх значень результативної ознаки.
2. Непараметричні методи зв’язку показників податкової діяльності. Взаємозв'язок окремих ознак у сфері податкової діяльності вимірюються також і за допомогою непараметричних методів зв'язку. Дослідження податкових явищ у багатьох випадках доцільно проводити, використовуючи різні умовні оцінки, до яких належать ранги. Вони являють собою ранговані (упорядковані досліджувані об'єкти на основі переваг) порядкові номери, розташовані у міру зростання або зменшення їх величин. Ці коефіцієнти обчислюються в тому разі, якщо досліджувані ознаки розподіляються за різними законами розподілу.
Наприклад, тій області, де рівень порушень податкового законодавства найнижчий, присвоюється ранг «І». Потім у міру збільшення цього показника, рангуються області, що досліджуються. Принцип нумерації значень досліджуваних ознак є основою непараметричних-методів вивчення взаємозв'язків податкових явищ і процесів.
У податковій статистиці серед наявних методів оцінки щільності зв'язку найчастіше використовують рангові коефіцієнти Спірмена (ς) та Кендалла (τ). Їх застосовують для визначення щільності зв'язку між якісними та кількісними ознаками, коли вони проранговані залежно від зростання або зменшення ознаки.
Ранговий коефіцієнт кореляції Спірмена можна обчислити за такою формулою:
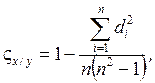(9.2)
де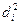 
— квадрат різниці рангів (факторної Rx та результативної Ry ознак);
п — кількість рангів.
Значення коефіцієнта Спірмена перебуває в межах від -1 до +1 (тобто одночасно оцінює щільність зв'язку та вказує його напрямок). Значущість цього показника перевіряється за допомогою t-критерію Стьюдента. При цьому використовують таку залежність:
(9.3)
Коефіцієнт кореляції вважається істотним, якщо tф > tкр, (a; к= η - 2) (див. додаток 29).
При стохастичній залежності кожному, значенню факторної ознаки відповідає множина значень результативної ознаки. Одиниці сукупності з даним рівнем факторної ознаки мають неоднакові значення результативної ознаки і утворюють розподіл за цією ознакою. Розподіл одиниць сукупності за однією ознакою при фіксованому значенні другої називається умовним. У табл. 9.1 наведено комбінаційний розподіл порушників податкового законодавства за кількістю порушень залежно від статі.
Таблиця 9.1
Розподіл порушників податкового законодавства за кількістю порушень залежно від статті (дані умовні)
| Стать | Кількість порушень податкового законодавства, чол. | Усього | ||||
| Жінки | — | |||||
| Чоловіки | ||||||
| Разом |
Зв'язок між ознаками стохастичний, і кожному значенню факторної ознаки:— статі порушників податкового законодавства — відповідає ряд значень результативної ознаки — кількості порушень. Кожен рядок таблиці являє собою ряд розподілу кількості порушень податкового законодавства при фіксованій кількості порушень, тобто характеризує умовний розподіл.
У табл. 9.2 наведені частості умовних розподілів.
Таблиця 9.2
Частості розподілу порушників податкового законодавства за кількістю порушень залежно від статі (дані умовні)
| Стать | Кількість порушень податкового законодавства, % до загальної кількості | Усього | ||||
| Жінки | 30,0 | 50,0 | 10,0 | 10,0 | - | 100,0 |
| Чоловіки | 3,3 | 3,3 | 13,4 | 53,3 | 26,7 | 100,0 |
| Разом | 10,0 | 15,0 | 12,5 | 42,5 | 20,0 | 100,0 |
Частості першого і другого рядків різні. Питома вага чоловіків що порушили податкове законодавство, з більшою кількістю порушень вища, ніж жінок. Тобто за різними статями порушників умовні розподіли не збігаються, і ознаки залежні. Чим більша відмінність між умовними розподілами, тим більше ознаки пов'язані між собою. При незалежності ознак частості умовних розподілів збігаються і дорівнюють частотам розподілу всієї сукупності.
Для оцінки тісноти зв'язку між ознаками використовують коефіцієнт взаємної спряженості (співзалежності):
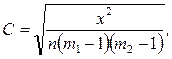(9.4)
де п — число одиниць сукупності;
т 1 і т 2, — кількість груп відповідно за першою і другою ознаками.
χ2 обчислюють за такою формулою:
(9.5)
де wіg — частості умовного розподілу в іншому рядку;
wі — частості розподілу в підсумковому рядку;
g — номер стовпця.
Очевидно, що при незалежності ознак 
. При функціональній залежності коефіцієнт взаємної спряженості досягає свого максимального значення. За даними табл. 9.2 (при підстановці у формулу відсотки замінені коефіцієнтами)
Тобто, щільність зв'язку між статтю порушників податкового законодавства і кількість порушень помітна.
Якщо результативна ознака кількісна, то з'являється можливість порівняти не тільки частості умовних розподілів, а й окремі їх характеристики, насамперед середні величини. Зв'язок між ознаками, який проявляється у зміні середніх величин умовних розподілів результативної ознаки при зміні значень факторної, називається кореляційним. Кореляційна залежність — це різновид стохастичного зв'язку. Якщо між ознаками існує кореляційний зв'язок, то існує і стохастичний (якщо середні величини умовних розподілів різні, то і самі розподіли різні). Якщо кореляційна залежність відсутня, то з цього не випливає, що ознаки незалежні (при однакових середніх умовні розподіли можуть відрізнятися, наприклад, рівнем варіації, ексцесом, асиметрією тощо).
Одним із найпоширеніших методів виявлення кореляційних зв'язків є метод аналітичних групувань.
Для побудови аналітичного групування, що характеризує залежність між двома ознаками, необхідно розділити досліджувану сукупність на групи за однією ознакою (як правило, факторною), а потім у кожній групі визначити середні значення другої ознаки, тобто середні умовних розподілів. Так, для побудови аналітичного групування за, даними таблиці 9.2 необхідно в кожній з груп за ознакою системи праці обчислити середній рівень порушень податкового законодавства.
Одержане аналітичне групування наведене в табл. 9.3.
Таблиця 9.3
Розподіл порушників податкового законодавства (дані умовні)
| Стать | Кількість порушень податкового законодавства, чол. | Середній рівень порушень |
| Жінки | ||
| Чоловіки | ||
| Разом |
Групування показує, що середня кількість порушень у чоловіків на 2 людини більше, ніж жінок, тобто між ознаками існує кореляційний зв'язок.
Як правило, при аналітичних групуваннях комбінаційні розподіли попередньо не будуються і групові середні розраховуються як прості середні арифметичні з індивідуальних варіант у групах.
У процесі дослідження залежності результативної ознаки від двох і більше, факторних ознак будуються комбінаційні аналітичні групування, які дають змогу вивчити залежність результативної ознаки від кожного із факторів при фіксованих значеннях інших факторних ознак.
За наявності залежності між ознаками у простому аналітичному групуванні від групи до групи змінюється не тільки рівень факторної ознаки, що лежить в основі групування, а й рівень інших пов'язаних з ним факторних ознак. У цьому разі зміну групових середніх не можна вважати результатом впливу тільки групової ознаки: вона відображає спільний вплив взаємопов'язаних факторів.
Це групування також дає можливість виявити взаємодію між факторами, яка проявляється і в неоднаковій силі впливу одного фактора на результативну ознаку при різних рівнях іншої факторної ознаки.
Виявивши за допомогою аналітичного групування наявність зв'язку між ознаками, необхідно встановити, яку роль відіграє досліджуваний фактор у зміні, результативної ознаки, належить він до головних чи другорядних.
Це завдання вирішується за допомогою вимірювання щільності зв'язку, в основі якого лежить складання варіації:
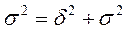(9.6)
Загальна дисперсія являє собою середній квадрат відхилень індивідуальних значень ознаки від загальної середньої (
). Ці відхилення викликані дією різних факторів, які впливають на досліджувану результативну ознаку х.
Середня із групових (залишкова) дисперсія δ2 — це середній квадрат відхилень індивідуальних значень ознаки χ від групових середніх — 
. Оскільки для усіх одиниць всередині кожної групи значення факторної ознаки є постійним, ці відхилення можуть бути пов'язані з впливом усіх факторів, окрім того, який покладений в основу групування.
Міжгрупова (факторна) дисперсія σ2 - це середній квадрат відхилень групових середніх від загальної середньої. Оскільки кореляційний зв'язок проявляється у зміні середніх значень результативної ознаки (групових середніх), то міжгрупова (факторна) дисперсія характеризує коливання результативної ознаки, пов'язаної зі зміною факторної ознаки.
Таким чином, правило складання варіації уможливлює виділення із загальної дисперсії результативної ознаки, пов'язаної з дією всіх факторів, двох складових:
• факторної дисперсії, пов’язаної з досліджуваною ознакою;
• залишкової, пов'язаної з іншими факторами.
Для характеристики щільності зв'язку в аналітичних групуваннях використовують кореляційне відношення:
(9.7)
Це показник частки вapiaцiї результативної ознаки, пов’язаної з факторною ознакою.
Кореляційне відношення коливається від 0 до 1. Якщо h2 i чисельник (факторна дисперсія) дорівнюють нулю, то групові середні piвнi між собою i при зміні факторної ознаки середнє значення результативної ознаки залишається незмінним.
Таким чином, при h2 = 0 кореляційний зв'язок між ознаками відсутній. При h2 = 1 факторна дисперсія дорівнює загальній, а залишкова — нулю. Це можливо за умови, якщо в кожній гpyпi всі індивідуальні значення результативної ознаки збігаються i кожному значенню факторної ознаки відповідає одне значення результативної. Отже, при h2 = 1 зв'язок між ознаками функціональний.
В аналітичному групуванні, наведеному в табл. 7.38, кореляційне відношення дорівнює 0,517. Це свідчить про те, що 51,7 % варіації середньої кількості порушень податкового законодавства пов'язано зі статтю порушників.
Відмінність кореляційного відношення від нуля ще не достатня для доказу icнyвання кореляційного зв'язку між ознаками. Відмінне від нуля кореляційне відношення може виникнути i при випадковому розподілі сукупності на групи. Наприклад, якщо виділити за алфавітним списком дві групи порушників податкового законодавства механічним способом (парні i непарні номери), то середня кількість порушень у цих двох трупах не збігатиметься i, таким чином, одержимо деяке відмінне від нуля кореляційне відношення. Але з цього не можна робити висновок про наявність зв'язку між середньою кількість порушень податкового законодавства i номером порушників у алфавітному списку. Групи відібрані випадковим способом i являють собою випадкові вибірки. Трупові середні, як вибіркові середні, містять похибки репрезентативності, i кореляційне відношення у цьому разі є мipoю таких похибок, а не характеристикою щільності зв'язку.
Щоб перевірити, чи не має визначене в аналітичному групуванні кореляційне відношення такої природи, тобто, чи не є воно результатом випадковості вибipки, необхідно порівняти фактичне значення h2 з тим максимально можливим значенням, що може виникнути у випадкових вибірках із генеральної сукупності, в якій зв'язок між ознаками відсутній i, таким чином, h2 = 0. Це максимально можливе значення (його називають критичним) необхідно розуміти як імовірнісне. Його доцільно вибирати так, щоб імовірність одержати у вибірці значення h2, що перевищує критичне (якщо в генеральній сукупності h2 = 0), була малою. Ця ймовірність називається рівнем значущості a. Як правило, у податковій статистиці використовуються рівні значущості l = 0,05 i l = 0,01. Критичне значення h2 при цих рівнях значущості є в спеціальних таблицях критичних значень h2 (див. додаток 30). Розподіл h2 у випадкових вибірках залежить від числа ступенів вільності факторної та залишкової дисперсій. Для факторної дисперсії число ступенів вільності k = m - 1 (де m — число груп), для залишкової дисперсії k2 = n - m (де n — число варіант; m — число груп). Наприклад, для аналітичного групування з таблиці числа ступенів скасування податкового покарання дорівнюють:
k1 = m – 1 = 2 - 1 = 1,
k2 = n - m = 40 – 2 = 38.
Критичне значення h2 знаходиться у додатку на перехресті стовпця, що відповідає k1, i рядка, що відповідає k2. Наприклад, при k1 = 1, i k2 = 38 для рівня значимості l = 0,05 критичне значущості h2 0,05 (1,38) = 0,097. Тобто, якщо зв'язок у генеральній сукупності відсутній (h2 = 0), то в 95 вибірках із 100 може виникнути кореляційне відношення, яке не перевищує 0,097, i лише у п'яти вибірках — таке, що перевищує 0,097. Рівень значущості — це настільки мала ймовірність, що процеси i явища податкової діяльності, які її мають, практично не можуть реалізуватися в одиничному випробуванні (іспиті). Отже, якщо в генеральній сукупності h2 = 0, то практично неможливо одержати значення h2, яке перевищує 0,097.
Якщо фактичне значення перевищує критичне, то це суперечить твердженню про відсутність залежності, i зв'язок муж ознаками визнається несуттєвим. У цьому прикладі фактичне значення кореляційного відношення h2 = 0,517 більше критичного h2 0,05 (1,38) = 0,097 i зв'язок між статтю порушників податкового законодавства i строком виплати податкових платежів є суттєвим.
Якщо фактичне значення h2 менше критичного, то це не суперечить твердженню про відсутність залежності, хоча i не доводить його правильність. Фактичне значення h2 могло бути одержане лише в ході вибірки із генеральної сукупності, в якій зв'язок відсутній, але це значення не обов'язково може бути одержане з такси сукупності. Висновок залишається невизначеним, а наявність або відсутність зв'язку не доведена. У ньому разі говорять, що зв'язок між ознаками несуттєвий.
При перевірці суттєвості зв'язку часто використовують не h2, а F-критерій (критерій Фішера), пов'язаний з h2 таким співвідношенням:
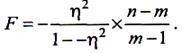(9.8)
Обчислити F-критерій можна також, виразивши його через дисперсії d2 і s2.
(9.9)
Критичні значення F наведені в додатку для l = 0,01 i l = 0,05. Правила використання цих таблиць i процедура перевірки за допомогою F- критерію нічим не відрізняються від описаних для h2.
При великих числах ступенів вільності F, на відміну від h2, майже не зміниться, тому побудову таблиць можна закінчити при k1 = 60, k2 = 120.
Для h2 необхідно було б побудувати аналогічні таблиці при великих k2.
У ході перевірки суттєвості зв'язку необхідно враховувати, що розподіл F i h2 у вибірках відповідає критичним значенням за умови використання ряду передумов, найважливішою з яких є передумова про нормальний розподіл сукупності за результативною ознакою.
Якщо ця передумова порушується, що досить часто зустрічається у правовій статистиці, то результати перевірки суттєвості зв'язку доцільно розглядати як приблизні.
При збільшенні обсягу сукупності зменшується вплив відхилення емпіричного розподілу від нормального на результати перевірки суттєвості зв’язку.
3. Поняття про кореляційний зв’язок у податковій статистиці. Явища та процеси, які відбуваються в суспільстві, зокрема у сфері податкової діяльності, взаємопов'язані і взаємообумовлені. Ці взаємозв'язки податкова статистика вивчає, використовуючи кореляційно-регресійний аналіз.
В основі такого аналізу податкової діяльності лежить припущення про те, що залежність між значеннями факторної ознаки та умовними середніми значеннями результативної ознаки може бути подана у вигляді функції:
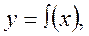(9.10)
яка називається рівнянням регресії. Розраховані за цим рівнянням очікувані середні значення результативної ознаки для.кожної (із рівнів) факторної ознаки х позначаються Y і називаються теоретичними, на відміну від емпіричних, тобто одержаних у результаті безпосередніх спостережень за значенням у.
Якщо аналітичне групування дає змогу виявити тільки наявність та напрямок зв'язку, то за допомогою рівняння регресії можна встановити, наскільки в середньому зміниться значення результативної ознаки при зміні факторної на одну одиницю.
Розрахунок рівняння регресії може вестися безпосередньо за первинними незгрупованими даними, тому кореляційно-регресійний аналіз податкової діяльності повніше використовує інформацію про досліджувані зв'язки, ніж метод групування. Але для розрахунку рівняння регресії необхідно, щоб обидві ознаки були кількісними (в аналітичному групуванні групувальна ознака може бути якісною).
Якщо результати аналітичного групування залежать від вибору інтервалів групування, то результати кореляційно-регресійного аналізу показників податкової діяльності в багатьох випадках залежать від вибору функції для розрахунку рівняння регресії.
Обчислення, пов'язані з використанням кореляційно-регресійного аналізу зв'язку двох ознак, що характеризують ту чи іншу сферу податкової діяльності, доцільно розділити на такі етапи:
• вибір форми рівняння регресії;
• розрахунок параметрів рівняння регресії;
• оцінка щільності зв'язку;
• перевірка суттєвості зв'язку.
З метою вибору форми рівняння регресії у податковій статистиці користуються такими прийомами.
Теоретичний аналіз базується на професійних знаннях дослідника про досліджуваний зв'язок. Щоб правильно застосувати кореляційний метод, необхідно глибоко розуміти сутність процесів взаємозв'язків, що відбуваються у сфері податкової діяльності. Важливо пам'ятати, що кореляційні методи не виявляють причин зв'язків між тими чи іншими податковими явищами, характер їх взаємодії, тобто не встановлюють причин залежності. їх роль зводиться до встановлення кількісної закономірності між досліджуваними ознаками і суцільністю зв'язку.
Але перш ніж визначити кількісну залежність досліджуваних ознак, необхідно встановити, який із досліджуваних показників є факторним, а який — результативним. Наприклад, якщо передбачається дослідити рівень порушень податкового законодавства в регіоні у зв'язку з чисельністю населення, то першочерговою виявиться можливість цього зв'язку, виходячи з реальної дійсності, а потім допускається, що факторним показником є чисельність населення, а результативним — рівень порушень.
У ході теоретичного аналізу показників податкової діяльності необхідно врахувати діапазон можливих значень факторної ознаки. Якщо в досліджуваній сукупності факторна ознака змінюється у вузьких рамках, то в полі її фактичної варіації відрізок кривої може бути наближений лінійним рівнянням.
4. Графічний аналіз зв'язку за допомогою кореляційного поля. При побудові графіка на осі абсцис позначаються значення факторної ознаки.v., а на осі ординат — результативної ознаки г. Кожна одиниця сукупності позначається на графіку крапкою. Коли є багато одиниць сукупності, доцільно попередньо побудувати аналітичне групування, винести на графік групові середні і з'єднати їх ламаною лінією. Побудована таким чином лінія групових середніх називається емпіричною лінією регресії.
Перебір функцій. Цей спосіб зумовлює обчислення рівняння регресії різних видів, а потім вибирають ті із них, яке найбільше відповідає емпіричним даним.
Запас функцій, які можуть бути використані для побудови регресії, досить обмежений. Для цього варто використовувати функції, лінійні щодо параметрів.
Розглянемо деякі функції, які застосовують в ході аналізу податкової діяльності частіше за інші:
а) лінійна — Y = а + bх.
Параметр а -лінійного рівняння регресії — це значення Y при х = 0. Якщо нуль перебуває в рамках фактичної варіації ознаки х, то а — одне із теоретичних значень Y, якщо ознака х у досліджуваній сукупності не приймає значень, близьких до 0, то параметр а не мас реального економічного змісту.
Параметр b називається коефіцієнтом регресії і показує, на скільки одиниць в середньому зміниться Y при зміні х на одиницю.
Рівняння регресії будь-якого виду доцільно розглядати тільки в рамках фактичної варіації факторної ознаки;
б) степенева— Y = а χb
Параметр b - степеневого рівняння називається коефіцієнтом еластичності. Він показує, на скільки відсотків зміниться значення результативної ознаки Y при зміні факторної ознаки x на 1 %; Параметр а значення Y при k = 1;
в) показникова — Y = аbx;
г) гіпербола — Y = а =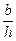 
;
д) парабола другого порядку — Y = а0 + а1x+ а2х2. Параметр а2 параболи другого порядку характеризує ступінь її кривизни. При а2 > 0 парабола має мінімум, при а2 < 0 — максимум. Степеневу та показникову функції приводять до лінійного вигляду шляхом логарифмування з наступною заміною змінних:
y' = lgx та
χ ' = lgχ.
Гіперболу та параболу перетворюють заміною змінних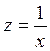 
та Z=x2.
5. Розрахунок параметрів рівняння регресії. Параметри рівняння регресії обчислюють методом найменших квадратів. Основна умова цього методу полягає в тому, що сума квадратів відхилень теоретичних значень Y від емпіричних повинна бути мінімальною:
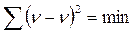(9.11)
Параметри рівняння регресії, які відповідають цій умові, розраховують шляхом рішення системи нормальних рівнянь. Ця система, наприклад, для лінійної функції (при обчисленні за незгрупованими даними) має такий вигляд:
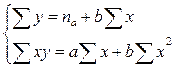(9.12)
Розв’язавши систему, одержуємо:
(9.13)
(9.14)
Використовуючи наведену методику, знайдемо параметри лінійного рівняння між рівнями порушень податкового законодавства (результативна ознака — у) та активності порушень (факторна ознака — х 1), значення яких наведені в табл. 9.4.
Таблиця 9.4
Вихідні показники для побудови регресійних моделей рівня порушень податкового законодавства
| Області н/п | Рівень порушень податкового законодавства. % (у) | Чисельність населення області, тис. чол. (х 2) | Частота порушень, % (х 1) |
| 40,8 | 12,9 | ||
| 41,3 | 14,8 | ||
| 32,5 | 10,7 | ||
| 10,0 | 12,0 | ||
| 34,7 | 14,5 | ||
| 38,9 | 11,3 | ||
| 45,7 | 15,0 | ||
| 38,8 | 17,1 | ||
| 35,9 | 10,5 | ||
| 36,9 | 11,6 | ||
| 38,0 | 12,0 | ||
| 31,1 | 9,5 | ||
| 28,5 | 8,2 | ||
| 25,6 | 10,4 | ||
| 24,4 | 9,6 | ||
| 30,0 | 10,5 | ||
| 17,0 | 7,5 | ||
| 29,0 | 10,7 | ||
| 34,0 | 7,3 | ||
| 25,0 | 7,7 |
Необхідні розрахунки наведені в табл. 9.4. Розв'язавши систему нормальних рівнянь
668,1 = 20 а о +223,8α1;
7741,13 =223,8 а о +2639,48 α1,
одержуємо:
Y= 11,458+1,961 χ1.
Параметри рівняння регресії можна одержати і за допомогою визначників:
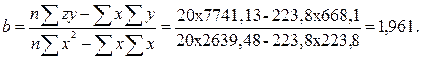
Коефіцієнт регресії показує, що підвищення частоти порушень на 1 % призводить до зростання рівня порушень податкового законодавства в середньому на 1,961 %. Оскільки у досліджуваній сукупності факторна ознака х не приймає значень, рівних або близьких до нуля, то параметр а не мас реального економічного змісту.
Щоб визначити очікувані теоретичні значення результативної ознаки (Y), підставимо в одержане рівняння регресії значення факторної ознаки по кожній обласній податковій адміністрації (гр. 6 табл. 9.5).
Якщо розрахунок ведеться на основі комбінаційного розподілу, то як варіант х і у використовують середини інтервалів, а всі задіяні в системі нормальних рівнянь величини зважують за частотами комбінаційного розподілу. У ході розрахунку параметрів рівняння регресії на основі аналітичного групування зважування проводять за частотами розподілу по факторній ознаці х1 (частоти розподілу по у відсутні). Щоб збільшити точність розрахунку, доцільно як факторну ознаку х використовувати середні значення показників у групах, а не показники середини інтервалів. Коли групування дискретне, результати розрахунку за згрупованими і незгрупованими даними збігаються.
6. Визначення щільності зв'язку між показниками податкової діяльності. Вимір щільності зв'язку в кореляційно-регресійному аналізі базується, як i в методі розкладання аналітичних групувань, на правилі розкладання варіації. Але як умовні середні, які характеризують вияв кореляційного зв'язку, виступають не групові середні, а теоретичні значення Y. Тому факторна дисперсія являє собою дисперсію теоретичних значень Y:
(9.15)
Для обчислення цієї дисперсії зручно користуватися формулою:
(9.16)
При її використанні не потрібно розраховувати теоретичні значення 7. Залишкова дисперсія характеризує величину відхилень емпіричних значень результативної ознаки у від теоретичних Y:
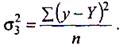(9.17)
Чим менше значення цієї дисперсії, тим ближче розташовані емпіричні значення до лінії peгpeciї. Сума цих двох дисперсій дорівнює загальній:
(9.18)
Таблиця 9.5
Табличний алгоритм розрахунку сум для визначення параметрів одно факторної та багатофакторної регресійних моделей
| № п/п | y | x1 | x1 y | x12 | y2 | y=11,458++1,961х1 | (Y-y)2 | x2 | x1 x2 | x2 у | x12 | у = - 0,939418 + + 1,471686 x1 + + 0,88503 x2 |
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 40,8 | 12,9 | 526,32 | 166,41 | 1664,6 | 36,76 | 11,256 | 2709,0 | 8568,0 | 36,6 | |||
| 41,3 | 14,8 | 611,24 | 219,04 | 1705,7 | 40,48 | 50,056 | 2930,4 | 8177,4 | 38,3 | |||
| 32,5 | 10,7 | 347,75 | 114,49 | 1056,3 | 32,44 | 0,931 | 1915,3 | 5817,5 | 30,5 | |||
| 40,0 | 12,0 | 480,00 | 144,00 | 1600,0 | 34,99 | 2,512 | 2640,0 | 8800,0 | 36,0 | |||
| 34,7 | 14,5 | 503,15 | 210,25 | 1204,1 | 39,89 | 42,055 | 3088,5 | 7391,1 | 39,2 | |||
| 38,9 | 11,3 | 439,57 | 127,69 | 1513,2 | 33,62 | 0,046 | 2938,0 | 10114,0 | 38,7 | |||
| 45,7 | 15,0 | 685,50 | 225,00 | 2088,5 | 40,87 | 55,726 | 4125,0 | 12567,5 | 45,4 | |||
| 38,8 | 17,1 | 663,48 | 292,41 | 1505,4 | 44,99 | 134,212 | 3420,0 | 7760,0 | 41,9 | |||
| 35,9 | 10,5 | 376,95 | 110,20 | 1288,8 | 32,05 | 1,836 | 2037,0 | 6964,6 | 31,6 | |||
| 36,9 | 11,6 | 428,04 | 134,56 | 1361,6 | 34,26 | 0,731 | 2610,0 | 8302,5 | 36,0 | |||
| 38,0 | 12,0 | 456,00 | 144,00 | 1444,0 | 34,99 | 2,512 | 2520,0 | 7980,0 | 35,2 | |||
| 31,1 | 9,5 | 295,45 | 90,25 | 967,2 | 30,09 | 10,989 | 2166,0 | 7090,8 | 33,2 | |||
| 28,5 | 8,2 | 233,70 | 67,24 | 812,3 | 27,54 | 34,398 | 1713,8 | 5956,5 | 29,6 | |||
| 25,6 | 10,4 | 266,24 | 108,16 | 655,4 | 31,85 | 2,418 | 1643,2 | 4044,8 | 28,3 | |||
| 24,4 | 9,6 | 234,24 | 92,16 | 595,4 | 30,28 | 9,766 | 1296,0 | 3294,0 | 25,1 | |||
| 30,0 | 10,5 | 315,00 | 110,25 | 900,0 | 32,05 | 1,836 | 1995,0 | 5700,0 | 31,3 | |||
| 17,0 | 7,5 | 127,50 | 56,25 | 289,0 | 26,17 | 52,345 | 1387,5 | 3145,0 | 26,4 | |||
| 29,0 | 10,7 | 310,30 | 114,49 | 841,0 | 32,44 | 0,931 | 1926,0 | 5220,0 | 30,7 | |||
| 34,0 | 7,3 | 248,20 | 53,29 | 1156,0 | 25,78 | 58,141 | 1350,5 | 6290,0 | 26,1 | |||
| 25,0 | 7,7 | 192,50 | 59,29 | 652,0 | 26,56 | 46,854 | 1532,3 | 4975,0 | 28,0 | |||
| Разом | 668,1 | 223,8 | 7741,13 | 2639,48 | 23273,5 | 668,10 | 519,551 | 45943,5 | 138158,7 | 668,1 |
Залишкову дисперсію часто обчислюють як різницю загальної та факторної дисперсій.
Для оцінки щільності зв'язку між показниками, що характеризують явища та процеси в сфері податкової діяльності у кореляційно-регресійному аналізі використовують аналогічний кореляційному відношенню за своєю побудовою коефіцієнт детермінації (R2), який виражається формулою:
(9.19)
У ході інтерпретації цього коефіцієнта необхідно враховувати, що він показує частку варіації, пов'язану з досліджуваним фактором, якщо визначено відповідне рівняння peгpeciї. Наприклад, якщо при вирівнюванні за лінійним рівнянням одержали значення R2 = 0,8, то це означає, що 80 % вapiaцiї результативної ознаки пов'язані з факторною ознакою.
Якщо рівняння peгpeciї обчислюється за аналітичним групуванням, то R2 £ h2.Рівність одержують, коли лінія регресії проходить через усі групові середні. При розрахунку R2 за не згрупованими даними ця нерівність може не виконуватись через варіацію факторної ознаки всередині груп.
Коефіцієнт детермінації R2, як і h2, коливається від 0 до 1. Якщо R2 = 0, то s2y = 0, тоді Y = у, i лінія peгpeciї перетворюється в пряму, паралельну oci абсцис.
При зміні значень факторної ознаки X значення результативної у не зміниться, i зв'язок між ознаками буде відсутній. Але в цьому разі йдеться про зв'язок, який має певне функціональне вираження, а не про кореляційний зв'язок взагалі. Можливо, в ході використання для рівняння peгpeciї iншoї функції буде виявлена висока щільність зв'язку.
Коли R2 = 1, залишкова дисперсія h2у = 0. Таким чином, емпіричні значення y i теоретичні Y збігаються, лінія peгpeciї встановлює точну відповідність між х та у, i зв'язок є функціональним. На практиці поряд із коефіцієнтом детермінації R2 для оцінки щільності зв'язку школи використовують квадратний корінь з нього, який називається індексом кореляції (R) і виражається формулою:
(9.20)
Розглянемо застосування цієї методики, використовуючи інформацію, наведену в табл. 7.40.
Для оцінки щільності зв'язку використаємо коефіцієнт детермінації. Його розрахунок, як уже було зазначено, заснований на розкладені загальної дисперсії результативної ознаки на дві складові: факторну i залишкову.
• Загальна дисперсія результативної ознаки:
= 1163,675 - 1115,894 = 47,781.
• Факторна дисперсія:
• Коефіцієнт детермінації:
Це означав, що 54,4 % варіації рівня порушень податкового законодавства мають лінійний зв'язок з показником рівня активності порушень. 1ндекс кореляції дорівнюватиме:
При вирівнюванні за лінійною функцією школи зручно використовувати ще один показник щільності зв'язку — лінійний коефіцієнт кореляції (r), який виражається формулою:
(9.21)
де 
(9.22)
— для не згрупованих даних; (9.23)
— для згрупованих даних; (9.24)
— для не згрупованих даних; (9.25)
— для згрупованих даних. (9.26)
У статистичній літературі для розрахунку лінійного коефіцієнта кореляції рекомендують й iншi формули, тотожні попередній:
або 
(9.27)
Значення лінійного коефіцієнта кореляції коливається від -1 до +1. Показник r із знаком «-» вказує на наявність оберненого зв'язку, a зі знаком «+» - прямого зв'язку. Таким чином, лінійний коефіцієнт кореляції дає не тільки оцінку щільності зв'язку, а й напрямок зв'язку. За абсолютною величиною цей коефіцієнт дорівнює індексу кореляції.
| r | = R.
Щоб одержати висновки про практичну значущість, значенням щільності зв'язку дається якісна оцінка. Бона визначається за шкалою Чеддока (табл. 9.6):
Таблиця 9.6
Pівні значущості щільності зв'язку за шкалою Чеддока
| Рівень щільності зв'язку | 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Характеристика сили зв'язку | слабка | помірна | помітна | висока | дуже висока |
Тобто, чим ближчий лінійний коефіцієнт кореляції до 0, тим менша щільність зв'язку, а чим ближчий він до 1, тим зв'язок щільніший.
Якщо щільність зв'язку між показниками, що характеризують податкову діяльність, перевищує 0,7, залежність у від х є високою, а при значеннях, які перевищують 0,9, — дуже високою.
Якщо лінійний коефіцієнт кореляції дорівнює 0, зв'язок між ознаками відсутній, якщо він дорівнює 1 — зв'язок функціональний.
Обчислимо лінійний коефіцієнт кореляції за даними табл. 9.4.
де
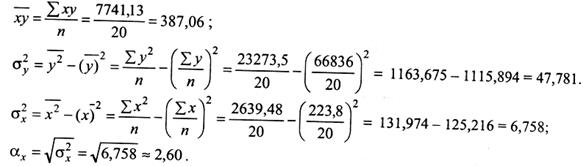
Таким чином, щільність між показниками рівня порушень податкового законодавства активності порушень в областях r = R = 0,73.
7. Побудова довірчих інтервалів. У ході кореляційно-регресійного аналізу показників податкової діяльності поряд з оцінкою суттєвості зв'язків важливе значення має побудова довірчих інтервалів для показників, які обчислюються. Це стосується i коефіцієнта peгpeciї. У невеликих за обсягом сукупностях значення цього коефіцієнта має схильність до випадкових коливань i можлива зміна у при зміні х на одиницю може бути задана тільки у вигляді певного інтервалу. Розрахунок цього інтервалу базується на тих самих принципах, що i обчислення довірчих інтервалів для середніх i частостей у вибірковому методі. Середня помилка коефіцієнта peгpeciї:
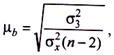(9.28)
а межі визначають відповідно до такої залежності:
b + / - t ´ mb,
де t — коефіцієнт довіри.
Визначимо середню помилку коефіцієнта peгpeciї:
Тоді гранична помилка з імовірністю 0,954 дорівнюватиме:
Dь = t mb = 2 ´ 0,423 = 0,846,
де t = 2 при Р = 0,954.
Звідси обчислимо межі довірчого інтервалу:
1,115 £ b1 £ 2,807.
Таким чином, з імовірністю 0,954 можна стверджувати, що середній рівень порушень податкового законодавства в областях із зростанням показника рівня активності порушень на 1 може досягти значень, не менших 1,115 i не більших 2,807 млн. грн.
Перевірка суттєвості зв'язку між показниками податкової доцільності в кореляційному аналізі проводиться за допомогою тих самих критеріїв, що i в аналітичних групуваннях. При визначені числа ступенів вільності зберігаютьсяформули, наведені ранiшe (k1 = m - 1; k2 = n - m), але в цьому разі m-число параметрів у рівнянні peгpeciї. Наприклад, для лінійного рівняння m = 2 i n =20. Якщо перевіряють за допомогою коефіцієнта детермінації, то критичні значення R2 визначають за тими таблицями, що i для h2. При використанні таблиць F- критерію користуються такою формулою:
(9.29)
За допомогою F- критерію можна перевірити суттєвість зв'язку між досліджуваними показниками. Для цього визначається число ступенів вільності:
k1 = m – l = 2 - l = l,
k2 = n – m = 20 - 2 = 18,
де т = 2 i n = 20.
Розраховується фактичне значення F- критерію:
Критичне значення F- критерію для рівня значущості a = 0,05 i ступенів вільності k1 = 1, k2= 18 становитиме F0,95(l’18) = 4,4 % (див. додаток 30).
Таким чином, фактичне значення F- критерію більше критичного значення (21,47 > 4,41), i з імовірністю 0,954 можна стверджувати, що між рівнями порушення податкового законодавства та активністю порушень досліджуваних обласних дирекцій банку існує лінійний зв'язок. Аналогічний висновок можна зробити при пepeвipцi суттєвості зв'язку за допомогою коефіцієнта детермінації R2. Критичне його значення R20,95 |1,18| = 0,197 (див. додаток 30) значно менше фактичного. Тому висновок про суттєвість зв'язку такий самий, як i за F- критерієм.
За допомогою F- критерію можна також перевірити правильність вибору форми рівняння регресії. Ця перевірка ґрунтується на зіставленні коефіцієнта детермінації R2, розрахованого на основі аналітичного групування, i кореляційного відношення h2. Як уже зазначалося, якщо лінія peгpeciї проходить через yci групові середні, то ці показники збігаються i в генеральній сукупності: R2 = h2. Фактичні значення F- кpитepiю в цьому разі обчислюють за формулою:
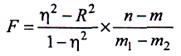(9.30)
де т1 — число груп;
т2 — число параметрів.
Якщо фактичні значення цього показника більші від критичних, то це говорить про неправильний вибір рівняння peгpeciї.
8. Множинна i часткова кореляції. Розглянуті методи побудови рівняння peгpeciї характеризують зв'язок між двома ознаками - x та y. Але у практичній податковій діяльності здебільшого використовують методи множинної кореляції, за допомогою яких досліджується зв'язок міжрезультативною ознакою у, двома i більше факторними ознаками х1, х2,..., хn.
Обчислюють параметри рівняння множинної кореляції також за допомогою системи нормальних рівнянь. Наприклад, для лінійного рівняння
у = а0 а1 х1 + а2х2 +... + аn хn. (9.31)
ця система має такий вигляд:
(9.32)
Коефіцієнти peгpeciї а1, а2, …, аn множинного рівняння показують, на скільки одиниць зміниться результативна ознака у при зміні відповідної факторної ознаки х на одиницю при фіксованих (середніх) значеннях х інших факторних ознак, що входять у рівняння peгpeciї. Тобто ці коефіцієнти показують вплив кожного фактора, очищеного (елюмінованого) від впливу інших факторів, що увійшли у рівняння. У цьому їx відмінність від коефіцієнтів парної peгpeciї, які можуть бути викривлені впливом взаємопов’язаних факторів.
Якщо ж фактори ознаки незалежні, то коефіцієнти множинної та парної peгpeciї збігаються. Тому будувати рівняння множинної peгpeciї доцільно за наявності взаємозв’язку факторних ознак. Оцінку щільності зв'язку між результативною ознакою та вciмa факторами проводять за допомогою сукупного коефіцієнта детермінації R2 у х1, х2,..., хn,який розраховують за тією формулою, що i при пapнiй кореляції.
Цей коефіцієнт характеризує частку вapiaцiї результативної ознаки у, пов’язаної з yciмa включеними в piвняння ознаками х1, х2,..., хn і відповідає вибраній формі зв'язку (наприклад, зв'язану лінійно).
Оскільки розрахунок теоретичних значень У при множинній кореляції досить гpoмiздкий, для обчислення факторної дисперсії зручно користуватися формулою, аналогічною формулі визначення s2n у парній кореляції:
(9.33)
У ході аналізу показників податкової діяльності поряд з оцінкою щільності зв'язку з усіма факторами одночасно при множинній кореляції оцінюють щільність зв'язку з кожною факторною ознакою окремо за допомогою часткового коефіцієнта детермінації. Розраховують цей коефіцієнт, наприклад для фактора х1, за схемою:
Нехай відомі сукупний коефіцієнт дeтepмiнaцiї в рівнянні зв'язку між результативним i всіма факторами показниками, окрім x1R2 у х1, х2,...., хn. Частка варіації у, не роз'яснена факторами х1, х2,...., хn, дорівнює 1 - R2 у х2, х3,...., хn, а частка варіації у, додатково роз'яснена включенням у рівняння peгpeciї фактора х1, дорівнює:
R2 y x1, x2, …, xn – R2 y x2, x3, …, xn. (9.34)
При включенні в рівняння додаткової змінної коефіцієнт детермінації не може зменшуватися, тому ця різниця завжди невід’ємна. Частка варіації результативної ознаки у, додатково роз’ясненої включенням у рівняння цього фактора, у варіації, не роз'ясненні іншими факторами, називається частковим коефіцієнтом детермінації.
Наприклад, для фактора х формула цього коефіцієнта має такий вигляд:
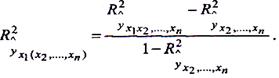(9.35)
Перевірка суттєвості сукупного коефіцієнта детермінації нічим не відрізняється від перевірки суттєвості коефіцієнта детермінації парної peгpeciї. Особливість перевірки суттєвості часткових коефіцієнтів детермінації полягає в підрахунку числа ступенів вільності.
Для залишкової дисперсії число ступенів скасування податкового покарання визначається за формулою:
k1 = п - т, (9.36)
а для факторної дисперсії число ступенів вільності дорівнює числу параметрів при певній змінній.
Наприклад, якщо даний фактор входить лінійно, то k1 = 1; якщо у вигляді параболи другого порядку, то k1, =2 (параметри при хі, та хі2).
Використовуючи дані попереднього завдання:
• розраховуються параметри лінійного рівняння peгpeciї, що характеризують залежність рівня порушень податкового законодавства (у) від рівня активності порушень (х1) i чисельності клієнтів банку (х2);
• вимірюється щільність зв'язку між цими показниками за допомогою часткових i сукупного коефіцієнтів детермінації;
• перевіряється суттєвість цих коефіцієнтів при рівні значущості a = 0,05.
Проміжні значення наведені в табл. 9.4.
Запишемо систему нормальних рівнянь для аналізованого прикладу:
668,1 = 20 а0 + 223 x1, + 4053 х2
7741,13 = 223 а0 + 2639,48 х1 + 45943,5 х2;
138158,7 = 4053 а0 + 45943,5 х1 + 840105 x2.
Розв'язавши систему лінійних рівнянь, одержуємо такі оцінки параметрів:
До а0 = - 0,939418; b1 = 1,471686; b2 = 0,088503.
Тоді рівняння peгpeciї, що характеризують залежність рівня порушень податкового законодавства від частоти порушень законодавства i чисельності населення областей, матиме такий вигляд:
Y= - 0,939418 + 1,471686 х1 + 0,088503 х2.
Часткові коефіцієнти регресії при факторах х1 та х2 показують, що при збільшенні частоти порушень законодавства на 1 % рівень порушення податкового законодавства в середньому зростає на 1,471 686 %, а при збільшенні чисельності населення в областях на 1 тис. чол., рівень порушень зростає на 0,088 503 %.
Проаналізувавши параметри одно факторного i багатофакторного рівнянь peгpeciї, побачимо, що частковий коефіцієнт при х1, який дорівнює 1,472 %, значно нижчий, ніж коефіцієнт при тій самій змінній у рівнянні парної peгpeciї, значення якого 1,961. Таке розходження пояснюється взаємозв’язками факторних ознак х1, х2.
Так, у рівнянні парної peгpeciї вплив на рівень порушення податкового законодавства частоти порушень законодавства не елюміновано. Але в цьому paзi на piвень порушень податкового законодавства впливає як частота порушень законодавства, так i чисельність населення в областях. Загальний їx вплив ефективніший i сприяє підвищенню порушень податкового законодавства. Зі зростанням чисельності населення збільшується i частота порушень законодавства.
У рівнянні багатофакторної peгpeciї при розрахунку часткового коефіцієнта peгpeciї b1, вплив частоти порушень на рiвень порушень податкового законодавства елюмінований i вважається незмінним, зафіксованим на середньому piвнi.
Аналогічно коефіцієнт peгpeciї b1що дорівнює 0,088 503, показує вплив чисельності населення на рівень порушень податкового законодавства, але не враховує вплив частоти порушень законодавства.
Обчислимо сукупний коефіцієнт детермінації R2yx1x2 . Для цього використаємо попередньо розраховане значення загальної дисперсії результативної ознаки (s2 = 47,781) i визначимо факторну дисперсію: 
Сукупний коефіцієнт детермінації становить:
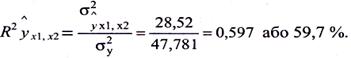
Розрахований показник R2yx1x2 показує, що 59,7 % коливань рівня порушень податкового законодавства досліджуваної сукупності лінійно зв'язані з розбіжностями частоти порушень законодавства та чисельності населення.
Побудуємо алгоритм розрахунку часткового коефіцієнта детермінації для ознаки х2. 3 цією метою використаємо попередні розрахунки, які стосуються побудови одно факторної моделі.
Обчислений сукупний коефіцієнт детермінації, як було зазначено, показує, що обидві факторні ознаки пояснюють 59,7 % вapiaцiї результативної ознаки у. У парній моделі ознака х1 пояснює 54,4 % вapiaцiї (коефіцієнт детермінації R2yx1 = 0,544).
Тобто включення в рівняння фактора х2 дало можливість пояснити 5,3 % вapiaцiї результативної ознаки y (R2yx1x2 …. R2yx1) = 0,597 - 0,544 = 0,053.
Оскільки факторна ознака х1 пояснює 54,4 % вapiaцiї результативної ознаки у, то максимально можлива частка вapiaцiї, яку можна обґрунтувати включенням х2 у piвняння, дорі
