| Спорттовари | Обсяг товарообігу званого періоду, тис. грн., p1q1 | Розмір зміни цін, % | Індивідуальні індекси цін, ip |
| Спортивний одяг | -2 | 0,98 (1 - 0,02) | |
| інвентар | +5 | 1,05 (1 + 0,05) | |
| Разом | — | — |
Обчислимо загальний індекс цін:
Товарообіг за рахунок зростання цін на спорттовари у звітному роцізбільшився на 2,6 %.
До розрахунку середніх індексів звертаються, коли відсутні необхідні дані для обчислення агрегатного індексу.
У податковій діяльності часто виникає необхідність проведення аналізу динаміки за сукупністю порушень податкового законодавства, у ході якого використовують формули, побудовані за методикою агрегатного індексу. Наприклад, відповідно до даних статистичної звітності «Звіт про порушення податкового законодавства і результати роботи» протягом січня було зафіксовано 25 випадків несплати податку на прибуток, 20 випадків несплати податку за землю, 56 ухилень від сплати податків, 32 випадки несплати ПДВ, а в лютому скоєні відповідні порушення податкового законодавства в кількості 18, 22, 61 та 43. Якщо кількість порушень податкового законодавства за їх видами помножити на їх бали (а це можуть бути й індивідуальні індекси), то одержимо умовну кількість порушень податкового законодавства. Тоді можна побудувати, наприклад, агрегатний індекс.порушення податкового законодавства (Іп.п.з.), який матиме такий вигляд:
(7.9)
де З0, З1 — кількість порушень податкового законодавства кожного виду відповідно в базисному та звітному періодах;
ƒ1 — бали грубості порушення податкового законодавства (бажано, щоб вони були одні і ті самі для обох періодів).
Тобто в нашому прикладі:
(7.10)
Індекс показує, що порушення податкового законодавства у лютому порівняно з січнем знизилася на 6 % завдяки зменшенню порушень податкового законодавства за видами.
Такий аналіз проводять як у динаміці, так і по регіонах, що дає можливість мати не тільки кількісну, а й якісну характеристику податкової діяльності. Використовуючи такі індекси, наприклад в разі рівної кількості порушень податкового законодавства, можна відстежити причину формування рівня порушень податкового законодавства в кожному регіоні, місті чи районі.
Аналогічно будуються й інші індекси податкової статистики. Наприклад, індекс покарань за порушення податкового законодавства (Іп.п.п.з.) має такий вигляд:
(7.11)
де В0, В1 — кількість осіб, що були оштрафовані за несплату податків відповідно в базисному і звітному періодах;
ƒ1 — бали порушення податкового законодавства.
За допомогою зіставлення індексів покарань за порушення податкового законодавства на основі рівня штрафів і реально призначених податковим органом строків сплати штрафів можна оцінити ступінь розбіжності податкової практики і положень чинного законодавства.
4. Для факторного аналізу динаміки середніх величин у податковій статистиці використовують індекси змінного, постійного складу і структурних зрушень.
Індекс середніх розмірів називається індексом змінного складу. Він показує зміну середньої величини, зумовлену дією двох факторів — змінами окремих рівнів показника і структури сукупності.
Індекс змінного складу можна розкласти на два аналітичних індекси-співмножники, кожний із яких відображає вплив тільки одного фактора. Один індекс-співмножник показує, як змінився б середній рівень показника за рахунок зміни індивідуальних рівнів якісного показника при постійній структурі сукупності, і називається індексом постійного складу. Інший індекс-співмножник показує, як змінився б середній рівень показника за рахунок зміни структури сукупності при збереженні базисних рівнів якісного показника. Це індекс структурних зрушень.
Індекс змінною складу дорівнює добутку індексу постійного (фіксованого) складу на індекс структурних зрушень:
(7.12)
Розглянемо розрахунок цієї системи індексів на прикладі (табл. 7.4).
Таблиця 7.4
Чисельність працівників податкових органів та рівень середньої зарплати
| Група працівників податкових органів | Базисний період | Звітний період | ||
| Середня місячна чисельність працівників податкових органів, чол. (Ч0) | Середня заробітна плата, грн. (3о) | Середня місячна чисельність працівників податкових органів, чол. (Ч1) | Середня заробітна, плата, грн. (31) | |
| Разом | - | - |
Обчислимо середню заробітну плату по двох і групах працівників у базисному і звітному періодах:
Індекс середньої заробітної плати (змінного складу) становить:
Середня зарплата працівників податкових органів у звітному періоді збільшилася на 19,3 % за рахунок одночасного впливу двох факторів — зміни середньої місячної заробітної плати по кожній групі працівників і зміни складу груп працівників (група працівників із меншою зарплатою знизилася з 43 до 39 % у звітному періоді порівняно з базисним). Індекс зарплати постійного складу дорівнює:
У середньому зарплата працівників податкових органів у звітному періоді підвищилася на 18,3 % порівняно з базисним тільки за рахунок динаміки середньомісячної зарплати кожної групи працівників (склад працівників постійний).
Обчислимо індекс впливу зміни структури сукупності на рівень зарплати:
де 
- середня зарплата працівників податкових органів у звітному періоді розрахована за середньомісячною зарплатою окремих груп працівників у базисному періоді.
Зміна структури (складу) працівників привела до зростання середньої зарплати у звітному періоді порівняно з базисним на 0,8 %.
Необхідно зазначити особливості застосування індексів у фінансово-податковій статистиці. Варто мати на увазі, що застосування загальних індексів у фінансово-податковій статистиці для характеристики середньої динаміки порушень податкового законодавства, які складаються із різних у якісному плані категорій, абсолютно неприпустиме. Обчислення середнього індексу за допомогою певних співмножників (скажімо, ваги податкових покарань) із числа таких різнорідних за економічною небезпекою порушень податкового законодавства, як ухилення від сплати податків тощо, було б типовим прикладом математичного формалізму повного ігнорування якісного аналізу.
Тому якщо обчислення загальних індексів допустиме в різних сферах економіки, промисловості, торгівлі та ін., так як тут якісно обґрунтовано застосування відповідних співмножників (ваг), то у податковій статистиці ніякі співмножники (ваги) не можуть усунути розходження між ухиленням від сплати різних видів податків.
Проте фінансистам часто доводиться мати справу з індексами у практиці податкових адміністрацій i податкових інспекцій, наприклад при розслідуванні справ про різні види ухилення від оплати податків.
Аналогічно розраховуються й індекси, що безпосередньо характеризують податкову діяльність. Наприклад, динаміку середнього рівня порушень податкового законодавства по регіонах можна аналізувати за допомогою такої індексної системи:
(7.13)
Даний індекс показує, як змінився середній рівень порушень податкового законодавства за сукупністю регіонів у звітному періоді порівняно з базисним:
(7.14)
Цей індекс показує, як змінився середній рівень порушень податкового законодавства за сукупністю регіонів у звітному періоді порівняно з базисним завдяки зміні рівня порушень у кожному регіоні.
(7.15)
Даний індекс показує, як змінився середній рівень порушень податкового законодавства за сукупністю регіонів у звітному періоді порівняно з базисним завдяки змінам, що відбулися у структурі чисельності населення peгioнiв.
Взаємозв’язок індексів:
(7.16)
де 
- індекс середнього рівня порушень податкового законодавства;
- індекс рівня злочинності;
IN - індекс структурних зрушень;
Рппз0, Рппз1 - рівень порушень податкового законодавства та чинники відповідно в базисному й звітному періодах;
3 - кількість зареєстрованих порушень податкового законодавства;
N - чисельність населення.
За допомогою зазначеної індексної системи визначають динаміку середнього piвня порушень податкового законодавства та чинники, що й породжують.
Знання індексів необхідне для орієнтування в ряді важливих економіко-податкових питань.
Контрольні питання:
1. Поняття статистичних індексів та їх класифікація в податковій статистики.
2. Які задачі індексного аналізі?
3. Які принципи побудови загальних індексів?
4. Що таке агрегатна форма індексів, що застосовується в податковій статистики?
5. Перетворення агрегатних індексів у середні.
6. Індекси постійного, зміного складу і структурних зрушень, які використовуються в податковій статистики.
7. Як вивчаються структурні зміниза допомогою індексного метода?
8. Які проблеми побудови територіальних індексів?
Рекомендована література:
Основна: [2,3,4,5,6,7,8]
Додаткова: [72,73,76,83,84,89]
ТЕМА 8
Вибіркове спостереження у податковій статистиці
План:
1. Суть вибіркового спостереження.
2. Обчислення помилок вибіркового спостереження. Систематичні помилки вибірки.
3. Різновиди відбору, що забезпечують репрезентативність вибірки.
1. Основною формою збору інформації з різноманітних питань оподаткування є державна статистична звітність податкових адміністрацій та податкових інспекцій.
Звітність включає найважливіші показники податкової діяльності.
Віддавна було привабливим не вивчати всі одиниці сукупності, а відбирати лише частину, за якою можна було б зробити висновки про властивості сукупності в цілому. З XVII ст. почав розвиватися й удосконалюватися метод вибіркового спостереження. Нині цей метод набув поширення й у податковій статистиці.
Оскільки дійсність швидко змінюється і на актуальні питання відповіді в офіційній статистичній звітності немає, економічна наука і практика систематично потребують інформації, що відображає цю дійсність. Таку інформацію можна одержати вибірковим спостереженням.
Вибіркове спостереження — науково обґрунтований вид не суцільного спостереження, при якому обстежується частина одиниць досліджуваної сукупності, відібрана за певними правилами, що дає змогу на підставі вибіркових оцінок отримати дані для характеристики сукупності в цілому.
Отже, при вибірковому спостереженні обстежується визначена, заздалегідь обумовлена частина сукупності 1/10; 1/20; 1/50 та ін., а результати поширюються на всю сукупність. Вибіркове спостереження набуло поширення, тому що має ряд переваг порівняно з суцільним спостереженням:
Ø потребує значно менше витрат праці, коштів, ніж суцільне спостереження;
Ø оперативніше за суцільне спостереження;
Ø дає змогу чіткіше організувати і провести спостереження і цим забезпечити більш точні результати, ніж при суцільному спостереженні дуже великої сукупності;
Ø дає можливість розширити програму спостережень і значно доповнити дані, отримані в результаті суцільного спостереження;
Ø може застосовуватися, коли неможливо провести суцільне спостереження через великий обсяг сукупності, або тому, що в результаті дослідження одиниці спостереження знищуються або псуються.
При вибірковому спостереженні мають справу з двома категоріями узагальнених показників: відносними і середніми. Відносні величини застосовуються для зведеної характеристики сукупності за альтернативними ознаками. Така характеристика дається у вигляді частки тих одиниць сукупності, що мають досліджувану очнику (частка порушників податкового законодавства, що мають вишу осипу; частка порушників податкового законодавства, що мають сім'ї, та ін.).
Узагальнюючими характеристиками сукупності за кількісною ознакою є середні величини.
Уся сукупність одиниць, із яких відбирають певну частину для вибіркового спостереження, називається генеральною сукупністю. Узагальнені показники генеральної сукупності називаються генеральними. Частина одиниць, відібраних для вибіркового спостереження, називається вибірковою сукупністю, а узагальнені показники — вибірковими.
Обчислимо узагальнені показники для генеральної і вибіркової сукупностей на прикладі.
За рік у районі виявлено порушників податкового законодавства 500 чоловік. Це генеральна сукупність. Розрахуємо узагальнені показники генеральної сукупності. За кількістю порушень на один суб'єкт оподаткування вони розподіляються так (табл. 8.1):
Таблиця 8.1
Групування порушників податкового законодавства за кількістю один суб'єкт оподаткування
| Кількість порушень податкового законодавства | Кількість порушників, ƒ | Середина інтервалу, х | х – а а = 7 | 
і = 2
| 
| 
| 
|
| До 4 | -4 | -2 | -40 | ||||
| 4-6 | -2 | -1 | -50 | ||||
| 6-8 | |||||||
| 8-10 | |||||||
| 10 і більше | |||||||
| Разом | - | - | - | - |
Обчислимо середній строк виплати податкових заборгованостей способом моментів:
Визначимо середнє квадратичне відхилення (а):
Знайдемо частку винних виплатити податкові заборгованості за 8 років і більше у загальній кількості порушників (w):
Ці показники можна визначити досить точно, але з меншими витратами і оперативніше за допомогою вибіркового спостереження.
Припустимо, із 500 чоловік відібрали у випадковому порядку 50 (10 %) і одержали такі результати (табл. 8.2):
Таблиця 8.2
Групування порушників податкового законодавства за кількістю порушників
| Кількість порушень податкового законодавства | Кількість порушників, ƒ | Середина інтервалу, х | х ƒ | 
| 
| 
|
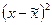
| До 4 | -4,8 | 23,04 | 69,12 | |||
| 4-6 | -2,8 | 7,84 | 51,80 | |||
| 6-8 | -0,8 | 0,64 | 7,04 | |||
| 8-10 | +1,2 | 1,44 | 34,56 | |||
| 10 і більше | +3,2 | 10,24 | 51,20 | |||
| Разом | - | - | - | 213,72 |
Обчислимо узагальнені показники вибіркової сукупності. Середній строк виплати податкових заборгованостей (
) становить:
Середнє квадратичне відхилення (σ) дорівнює:
Частка винних у виплаті податкових заборгованостей за 8 років і більше у загальній чисельності підібраних становить:
Порівняння узагальнених показників вибіркової сукупності з показниками генеральної показує, що вони не збігаються, але близькі до них.
Взагалі ці різниці могли бути й іншими, оскільки серед відібраних одиниць, якщо зробити відбір кілька разів, усякий раз може виявитися різне їx число в кожній гpyпi, а отже, i різні арифметичні значення середньої величини та середнього квадратичного відхилення. Відповідь на питання, наскільки велика i ймовірна різниця між узагальненими генеральними i вибірковими показниками, дає теорія вибіркового спостереження, що базується на законі великих чисел. Закон великих чисел, що випливає з теорії П. Чебишева щодо вибіркового спостереження, можна сформулювати так: з імовірністю, як завгодно близькою до одиниці, можна стверджувати, що при достатньо великій кількості спостережень зведені характеристики вибіркової сукупності як завгодно мало відрізнятимуться від зведених характеристик генеральної сукупності.
Точність результатів вибіркових досліджень багато разів перевірялась. Ці спостереження підтвердили, що результати досліджень, проведених вибірковим методом, дають досить точне уявлення про досліджувану сукупність i широко застосовуються на практиці.
2. Обчислення помилок вибіркового спостереження. Відхилення узагальнених показників вибіркової сукупності від зведених характеристик генеральної сукупності називається помилками вибірки, вони виникають внаслідок самого факту відбору. Структура вибіркової сукупності не може точно відтворити генеральну сукупність. Помилки, властиві вибірковому спостереженню, називаються помилками вибірки або репрезентативності. За своєю природою вони можуть бути систематичними і випадковими.
Систематичні помилки вибірки виникають при порушенні принципів проведення вибіркового спостереження. Наприклад, якщо при обстеженні успішності студентів відібрати для спостереження сильну групу, то середній бал буде завищений.
Систематичні помилки спрямовані тільки в один бік (або зменшення, або збільшення) і призводять до того, що вибіркове спостереження втрачає свій сенс, тому що на його основі не можна правильно визначити показники генеральної сукупності. Систематичних помилок можна уникнути. Для попередження й усунення їх потрібно встановити науково обґрунтований порядок відбору, який проводиться випадковим методом, коли кожній одиниці генеральної сукупності забезпечена однакова можливість потрапити у вибірку.
Якщо відбір зроблено правильно, то розбіжності між узагальненими показниками вибіркової і генеральної сукупностей виникають через сам факт відбору і називаються випадковими помилками вибірки.
Випадкові помилки дають відхилення як в один, так і в інший бік. Вони властиві вибірковому спостереженню, усунути їх практично неможливо, але можна обчислити.
Помилка вибірки залежить від чисельності вибіркової сукупності і ступеня варіації досліджуваної ознаки. Чим більше одиниць відібрано у вибіркову сукупність, тим меншими, за інших рівних умов, будуть розбіжності. Чим менша варіація ознаки, тим менша помилка вибірки. Залежність ця виражається у формулі середньої помилки вибірки (μ).
При повторному відборі:
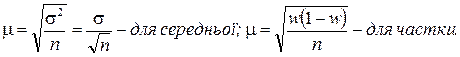(8.1)
При повторному відборі
(8.2)
де σ2 — дисперсія ознаки в генеральній сукупності;
п — число одиниць вибіркової сукупності;
N — число одиниць генеральної сукупності;
w — частка одиниць, що мають певні ознаки.
Отже, для визначення середньої помилки вибірки потрібно знати дисперсію ознаки в генеральній сукупності. Але при вибірковому спостереженні генеральна дисперсія невідома.
У курсі математичної статистики доведено, що
(8.3)
У міру зростання числа вибірки 
коефіцієнт наближається до одиниці, і розбіжності між генеральною та вибірковою дисперсіями стають меншими. Тому середню помилку вибірки можна обчислити, виходячи зі значення вибіркової дисперсії.
Середня помилка вибірки характеризує міру відхилень вибіркової середньої від генеральної середньої, частки вибіркової від частки генеральної.
Обчислимо для нашого прикладу середні помилки вибірки. Для середньої величини:
при повторному відборі (див. табл. 8.2):
при безповторному відборі:
Отже, середній строк виплати податкових заборгованостей у генеральній () сукупності становить від 7,5 до 8,1 року (
):
Це можна стверджувати з імовірністю 0,683, тобто якщо буде відібрано 1000 порушень податкового законодавства, то 683 з них матимуть середній строк виплати податкової заборгованості в цих межах. Точність розрахунку можна гарантувати на 68,3%.
Визначимо середні помилки вибірки для частки порушників податкового законодавства на 8 i більше місяців.
При повторному відборі (див. табл. 7.32)
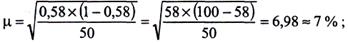
При без повторному відборі:
Обчислені помилки кількісно майже не відрізняються i показують, що частка порушників податкового законодавства, винних у сплаті борги за 8 i більше років, у вибірковій сукупності відхиляється від частки у генеральній на ±7 %.
Отже, з імовірністю 0,683 можна стверджувати, що питома вага порушників на 8 i більше місяців у генеральній сукупності становитиме від 51 до 65 %:
P = w ± m = 58% ± 7%,
51 % £ Р £ 65%.
Розраховані з імовірністю 0,683 показники не завжди влаштовують дослідників.
Щоб підвищити iмовіpність, потрібно розширити межі відхилень, прийнявши за міру, скажімо, подвоєну помилку вибірки (2 m). У цьому разі ймовірність нашого твердження досягне 0,954, а середній строк виплати податкових заборгованостей становитиме від 7,2 до 8,4 місяця:
х = х ± 2m = 7,8 ± 2 х 0,3 = 7,8 ± 0,6;
7,2 £ х £ 8,4 місяця.
Частка винних у виплаті податкової заборгованості за 8 i більше місяців становитиме від 44 до 72 %:
P = w± 2m = 58% ± 2 x 7 = 58 ± 14;
44% £ Р £ 72%.
Помилка вибірки, обчислена з імовірністю, більшою ніж0,683, називається граничною й визначається за формулою:
D = t m, (8.4)
де D - гранична помилка вибірки;
t - коефіцієнт кратності помилки (коефіцієнт довіри).
Коефіцієнт довіри залежить від імовірності, з якою можна гарантувати, що гранична помилка вибірки не перевищить t - кратну середню помилку. Коефіцієнт t визначається за таблицями значень інтеграла ймовірностей. Так, при ймовірності 0,954 - t = 2, aпри ймовірності 0,997 - t = 3.
Наведені формули помилок вибірки дають змогу заздалегідь розрахувати той обсяг вибірки, при якому відхилення вибіркових показників від генеральних не перевищать заздалегідь заданих розмірів, що гарантуються з визначеною ймовірністю.
Повторний відбір: Без повторний відбір:
— для середньої, 
— для середньої,
— для частки. 
— для частки.
Наприклад, потрібно визначити кількість працівників податкових інспекцій, щоб встановити середнє навантаження (середню кількість справ) на одного податківця. Помилка вибірки з імовірністю 0,954 не повинна перевищувати ±5 справ при середньому квадратичному відхиленні ±20 справ:
Отже, потрібно відібрати 64 податківці для визначення середньої кількості справ, що припадає на одного податківця.
В економічній практиці домінуюче значення має вивчення якicниx (атрибутивних) ознак, i для обчислення середньої помилки вибірки використовують такі формули:
при повторному відборі: 
(8.5)
при без повторному відборі: 
(8.6)
Наприклад, iз сукупності 900 порушників податкового законодавства по району у випадковому порядку досліджували 100 суб’єктів оподаткування, ізних 80 скоїли порушення навмисно. Потрібно визначити з ймовірністю 0,954 частку порушників податкового законодавства, які скоїли порушення навмисно.
Обчислимо граничну помилку частки:
Визначимо межі частки:
Р = w ± D = 80% ± 7,4%;
72,6 % £ Р £ 87,4 %.
Отже, з iмовipнiстю 0,954 можна стверджувати, що від 72,6 до 87,4 % із 900 порушників податкового законодавства скоїли порушення навмисно.
3. Найважливішою умовою проведення вибіркового спостереження є правильний відбір одиниць сукупності:
• достатня кількість відібраних одиниць;
• об’єктивний відбір, що забезпечує однакову можливість кожній одиниці сукупності потрапити у вибірку.
Вибіркова сукупність повинна бути утворена на основі випадкового відбору. Розрізняють такі основні види відбору:
• власне випадковий,
• механічний;
• розшарований.
За кількістю охоплених одиниць сукупності розрізняють великі і малі вибірки.
Власне випадковий відбір полягає у тому, що спостереження ведеться за частиною одиниць сукупності, відібраною з усієї сукупності у випадковому порядку, ненавмисно. Випадковий відбір дає лотерея або жеребкування. На кожну одиницю сукупності заготовляють жетон, квиток із номером. Потім у випадковому порядку відбирають необхідну кількість жетонів (одиниць сукупності).
Випадкова вибірка може бути повторною i без повторною.
Повторним називається такий відбір, при якому кожна одиниця сукупності бере участь у відборі стільки разів, скільки відбирається одиниць. Без повторний - це відбір, при якому відібрана одиниця надалі не бере участі у відборі.
Механічний відбір полягає у тому, що вся сукупність одиниць розбивається на рівні за обсягом групи з випадковими ознаками, потім із кожної групи, як правило, випадковим порядком відбирається одна одиниця. Механічний відбір — різновид власне випадкового відбору, але має ряд організаційних переваг (легше i простіше організувати перевірку відбору одиниць сукупності).
Він буває тільки без повторним i організується у такий спосіб. Наприклад, потрібно з 1000 порушників податкового законодавства відібрати 100 для вивчення залежності тяжкості порушення від наявності освіти. Складають алфавітні списки вcix порушників податкового законодавства. Визначають інтервал, що дорівнює 10 (1000 / 100). За складеним списком, починаючи з будь-якого номера, у межах першого десятка відбирають у випадковому порядку одного порушника. Якщо з першого десятка випадковим добором відібрали порушника податкового законодавства під номером 5, то далі відбирають 15-го, 25-го, 35-го i т. д.
Механічний відбір можна також застосувати, використовуючи природний порядок розташування одиниць генеральної сукупності (розподіл засуджених на ланки, групи тощо).
Розшарований відбip починають з групування вciєї сукупності на якісно однорідні групи за істотною, типовою ознакою (наприклад, групування порушників податкового законодавства за видами порушень).
Потім iз кожної групи власне випадковим або механічним способом відбирають Кількість одиниць пропорційно питомій вазі групи в усій сукупності. Розшарований відбір доцільно застосовувати при великій міжгруповій варіації. При цьому відборі досягається більш повне представництво у вибірці окремих типів досліджуваного явища, тому він дає точніші результати, ніж власне випадковий i механічний.
Крім того, у податковій статистиці використовують i такі види відбору, як серійний, моментний, багатоступеневий, багатофазовий. Різні форми організації відбору, як одиниць у вибіркову сукупність, - це подальший розвиток та видозміна простого випадкового відбору. Застосування того чи іншого виду відбору визначається особливим характером об’єкта спостереження з метою здешевлення або полегшення процесу спостереження.
Контрольні запитання:
1. Суть вибіркового спостереження, яке використовується в податковій статисттиці.
2. Методи обчислення помилок вибіркового спостереження в податковій статисці.
3. Різновиди відбору, що забезпечують репрезентативність відбірки в податковій статисці.
Рекомендована література:
Основна: [7,8,27,34,40,46]
Додаткова: [66,70,76,79,82,83,89]
ТЕМА 9.
