У лінійних колах змінного струму синусоїдально перемінні струми і напруги визивають періодичні зміни енергії, що були запасені в електричному полі конденсаторів 
та в магнітному полі котушок 
. Отже, в колах протікають струми і є напруги, що змінюють ці енергії, і всі процеси стають значно складнішими, ніж в колах постійного струму. При цьому елементи з параметрами L і C обмінюються енергіями між собою та з джерелом, і частина енергії вживається на активних опорах.
Таким чином, режим роботи визначається сукупністю режимів трьох ідеальних елементів: R, L і C, особливості поведінки яких в колах синусоідального струму наведено в табл. 5.1. Ці особливості витікають з основних зв’язків між напругами та струмами:
Таблиця 5.1- Результати замірів
| Характеристики | R | L | C |
1 Напруги на затисках при синусоїдальному струмі
|
|
|
|
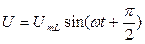
| 2 Закон Ома для відрізка кола | 
| 
| 
|
| 3 Кут зсуву фаз напруги та струму |
| 
| 
|
| 4 Активна потужність, що виділяється в елементі | 
| ||
| 5 5. р в символічній форміи і струмуьному ve ідальнгого енергії, і всі процеси стають значно у полі конденсаторів Реактивна потужність елементу |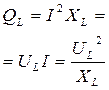 
| 
|
Продовження таблиці 5.1
| 6 Векторна діаграма напруги і струму | 
| 
| 
| ||
| 7 Опір в символічній формі | 
| 
| 
|
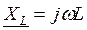
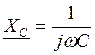
Елементи з параметрами L і C називають реактивними елементами.
Помітим, що кут зсуву фаз є алгебраїчною величиною і його знак визначає характер навантаження: індуктивний, якщо φ>0, і ємнісний при φ<0.
При послідовному з’єднанні трьох вищеназваних ідеальних елементів (рис.5.1) для миттєвих значень за другим законом Кирхгофа маємо
і в геометричній формі -
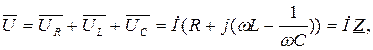
де Z – комплекс повного опор кола,
,
де 
- модуль повного опору;
φ – кут зсуву фаз, що визначається для заданої частоти параметрами кола,
де 
- реактивні опори кола, визначають характер кола.
 |
Рисунок 5.1 – Послідовне з’єднання RLC - елементів
Якщо XL>XC, кажуть, що індуктивність домінує в колі, коло має індуктивний характер і φ>0.
Якщо XL<XC, φ<0, коло носить ємнісний характер (рис.5.2).
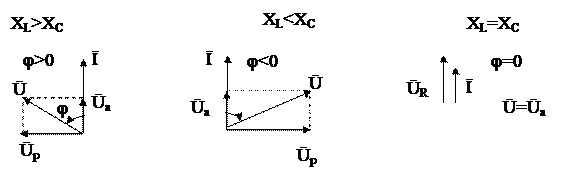
Рисунок 5.2 –Векторні діаграми струму та напруги
Розклавши вектор напруги на составні, одна з яких збігається зі струмом, а друга йому перпендикулярна, одержують активну і реактивну составні напруги при цьому.
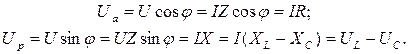
Таким чином, для будь якого кола мають векторну діаграму напруг (трикутник напруг). Поділивши усі сторони цього трикутника на загальний для всіх елементів струм, чи перемножив їх на той же струм, одержують ще два подібних трикутника, сторони яких у відповідному масштабі будуть у першому випадку опори і в другому – потужності. Наприклад, для індуктивного характеру навантаження ці трикутники подані на мал. 5.3.
а) б) в)
а) трикутник напруг; б) трикутник опорів; в)трикутник навантаження
Рисунок 5.3 – Векторні діаграми
Аналіз послідовного з’єднання має на увазі справедливість другого закону Кірхгофа та інших співвідношень для електричних кіл, але в геометричній формі. Аналіз проводиться звичайно при розкладі напруг на активні і реактивні составні, які з урахуванням характеру відрізків (індуктивний чи ємнісний) будуються на векторній діаграмі.
Векторні діаграми підвищують наочність результатів аналізу. При розрахунку цих составних необхідно знати параметри приймачів.
Якщо приймач має тільки один параметр (наприклад резистор, що має тільки активний опір), то величина 
визначається за законом Ома чи 
, тобто для визначення параметру необхідно заміряти струм і напругу чи струм і потужність приймача.
У приймачі двох параметрів, наприклад котушки параметрів R і L, останні назначаються експериментально двома методами.
Перший полягає у визначенні опору Rк в колі постійного струму. Для цього котушку вмикають в коло постійного струму і замірюють опір котушки 
і вважають його надалі активним опором котушки. На низьких частотах, де поверхневий ефект та ефект близькості проявляються слабо, це допускається.
Визнавши Rк, вмикають в коло змінного струму і визначають повний опір котушки 
. Далі вираховують:
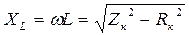та 
.
Другий метод використовується частіше, але для цього методу потрібен ватметр. Вмикають котушку в коло змінного струму відомої частоти та заміряють напругу Uк, струм Iк і потрібну активну потужність Pк.
Відомо, що
де cosφк визначають з формули потужності 
.
Тоді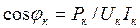 
, а 
. Далі 
.
Окремим випадком є режим кола, в якому XL=XC, тобто 
або 
. У такому випадку X=XL-XC=0, відповідно φ=0 та Z=R, тобто коло веде себе як активний опір. Такий режим кола називається резонансом напруг. При цьому в колі на окремих елементах мають місце реактивні потужності QL=I2XL і QC=I2XC, але реактивна потужність, що вживається з сіті дорівнює нулю. Зазначимо, що при X=0 повний опір Z=Rє мінімальним. Звідси струм має максимальне значення і реактивні напруги UL=IXL і UC=IXC можуть бути значними і навіть перевищувати напругу джерела. При умові XL=XC>>R напруга на реактивних елементах UL=UC>>UR=U, і в такому випадку говориться про перенапругу на елементах з параметрами L і C. Описаний режим, при якому ω2LC=1,може бути одержаний шляхом зміни параметрів L або C або зміною частоти постачальної напруги до величини 
називають власною частотою кола.
У лабораторних умовах про проходження точки резонансу при зміні параметрів, наприклад С, роблять висновок про змін струму.
