В пояснительной записке следует изложить теоретический материал по рассматриваемому типу колебаний, разобрать типовые задачи. Затем на основе задач из сборника И.Е.Иродова «Задачи по общей физике» или проделанного эксперимента выбрать параметры и в расчетной части построить требуемые графики.
Вначале дадим вводные замечания для повторения школьного курса физики по разделу колебаний, а затем рассмотрим более сложный материал.
В физике, в технике, в природных и социальных явлениях часто происходят такие процессы, когда ускорение (скорость изменения скорости) определенной характеристики процесса (физической величины) пропорциональна значению этой величины и направлена против ее изменения (например, в данный момент времени). Такая общность явлений находит свое отражение в едином математическом аппарате их описания. Все эти процессы описываются одним дифференциальным уравнением, решением которого является функциональные зависимости, основным свойством которых является периодичность, повторяемость.
Ввиду того, что в технической литературе в различных пособиях и используются различные обозначения величин и термины, характеризующие колебательные процессы, дадим кратко основные определения и понятия на основе принятых базовых учебников. В работе следует использовать именно эти обозначения, понятия, определения.
В природе часто наблюдается такое движение, когда тело, перемещаясь по замкнутой траектории, возвращается в исходное положение через равные промежутки времени. Такое движение называется периодическим, а промежуток времени, по истечении которого движение повторяется, называется его периодом Т. Величина, обратная периоду, называется частотой. Частота f = 1/Т показывает, сколько раз в секунду повторяется движение. Единица измерения частоты, соответствующая периоду Т = 1с, называется герцем (Гц): 1Гц = 1с-1
Существует, очевидно, бесчисленное множество различных видов периодического движения. Мы будем рассматривать простейший случай периодического движения материальной точки вдоль определенной кривой: в этом случае говорят, что частица совершает одномерное движение, т.е. она обладает одной степенью свободы. Для задания положения частицы в таком случае достаточно всего одной координаты; в качестве таковой можно выбрать, например, расстояние вдоль кривой от некоторой точки, используемой в качестве начала отсчета. Обозначим эту координату буквой х. Силы, действующие на частицу, в этом случае будут зависеть от этой единственной координаты.
Гармонические колебания
Поскольку простейшими периодическими функциями являются тригонометрические функции синус и косинус (их период равен 2π), то простейшим одномерным периодическим движением будет такое движение материальной точки, при котором ее координата х изменяется по закону
x(t) = A cos(ω0t + α), x(t) = A sin(ω0t + α1), (1)
где А, ω0, α, α1 – некоторые постоянные величины.
Такое периодическое движение называется гармоническим колебательным движением, а частица (материальная точка), совершающая гармонические колебания, - гармоническим осциллятором. Термины «маятник», «осциллятор», «колебательная система» будем считать тождественными.
Величины А и ω0 имеют простой физический смысл. Так как период косинуса и синуса равен 2π, то период движения Т (период колебаний) связан с ω0 соотношением
T = 2π/ω0. (2)
Это соотношение легко получить из условия, что частица в моменты времени t и (t + T) имеет одинаковые координаты
х (t) = (t + T). (3)
Из (3) и (1) вытекает, что
ω0 = 2π/T = 2π ν. (4)
Величину ω0 называют циклической (круговой) частотой. Единица измерения циклической частоты - радиан в секунду (рад/c), ν – частота колебания, измеряемая в герцах (Гц).
Максимальное значение координаты х называется амплитудой колебания. Так как максимальное значение косинуса и синуса любого переменного аргумента равно единице, то максимальное значение координаты х при гармонических колебаниях равно А (рис. 1)
Аргумент косинуса или синуса в (1)
φ (t) = ω0t + α (5)
называют фазой колебаний. Из (5) следует, что при t = 0
α = φ, (6)
поэтому постоянную величину α называют начальной фазой.
Из (1) (мы будем везде в дальнейшем преимущественно использовать первую формулу для х(t)). Легко найти скорость частицы, совершающей гармонические колебания. Взяв производную по времени от первого выражения из (1), получим
vx = dx/dt = -A ω0 sin (ω0t + α) = A ω0 cos(ω0t + α + π/2). (7)
Как видим, при гармонических колебаниях скорость частицы изменяется также по гармоническому закону, но изменение скорости ”опережает по фазе ” изменение координаты на величину 1/2 π. Иначе говоря, разность фаз колебаний скорости и координаты равна 1/2 π. При этом в те моменты времени, когда координата x достигает экстремальных значений ± А, скорость частицы обращается в нуль, и наоборот. Максимальное по модулю значение скорости (ее амплитуда) равно
vmax = A ω0. (8)
Выясним, какова должна быть результирующая сила Fx = 
действующая на частицу, чтобы она совершала гармонические колебания. Найдем для этого ускорение частицы при таком движении. Продифференцировав (7) по времени, получим
ax = 
= - A ω2 0 cos(ω0t + α), (9)
или с учетом фазы относительно (1)
ax = - ω0 2x = A ω2 0 cos(ω0t + α + π). (10)
Если учесть второе выражение в (1), то получим результаты, представленные в табл. 1.
Таблица 1
Описание кинематических характеристик колебаний
| 1. x(t) = A sin (ω t + φ) 1. 2. v = x'(t) = ω A cos(ω t + φ) 2. 3. a = v'(t) = - ω2 A sin (ω t +φ) | 1. x(t) =A cos(ω t + φ) 2. v = x'(t) = - ω A sin(ω t + φ) 3. a = v'(t) = - ω2 A cos(ωt + φ) |
| φ = 0 | |
4. x(t) = A sin ∙ ω t
5. v = ω A cos ω t = ω A sin (ω t +  ) = ω A(sin ω t · cos + cos ω t · sin ) = ω A cos ω t
6. a = - ω2 A sin ω t = ω2 A sin(ω t + π)
| 4. x(t) = A cos ω t
5. v = - ω A sin ω t = ω A·
cos(ω t + ) = ω A(cos ω t · cos -sin ω t · sin ) = - ω A× ×sin ω t
6. a = - ω2 A cos ω t = ω2 A ×
cos (ω t + π)
|
7. tg φ =  ; A2 = 
| 7. tg φ = -  ; A2 =
|
8. A cos ω t + B sin ω t =  cos(ω t – δ)
| |
cos δ = 
| sin δ = 
|
| 9. A cos ω t + B sin ω t = sin(ω t + δ)
| |
| sin δ =
| cos δ =
|
Из (10) видно, что ускорение изменяется со временем по такому же закону, что и координата частицы, но фаза колебаний ускорения отличается от фазы координаты на π. Наибольшее по модулю значение ускорения (его амплитуда)
amax = A ω02. (11)
Из второго закона Ньютона для движения частицы массой m
m 
= 
= 
,
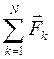записанного в проекции на направление движения частицы с учетом (10) получим
maх = Fx, Fx = -m ω0 2x. (12)
Таким образом, для того чтобы частица совершала гармонические колебания, действующая на нее результирующая сила должна быть пропорциональна величине смещения частицы и направлена в сторону, противоположную этому смещению. Такую силу называют восстанавливающей (или возвращающей).
Зависимость силы от положения частицы в виде (12) встречается в физических задачах очень часто. Если какое-либо тело находится в положении устойчивого равновесия (пусть это будет точка x = 0), то в этом положении = 
= 0, а при этом смещении тела из этого положения в ту или другую сторону возникает отличная от нуля результирующая сила , действующая на тело и стремящаяся вернуть его в положение равновесия. При этом график зависимости Fx (x) будет иметь вид некоторой кривой: в точке x = 0 сила Fx = 0, а по обе стороны от этой точки она имеет противоположные знаки (рис. 2).
В общем случае зависимость возвращающей силы от x не является линейной. Это означает, что хотя тело и будет совершать колебания около положения равновесия, но колебания не будут гармоническими. Однако при небольших смещениях тела из положения равновесия отрезок кривой Fx вблизи x = 0 можно всегда приближенно заменить отрезком прямой линии так, что сила Fx окажется пропорциональной величине отклонения x, и колебания тела будут гармоническими. Частота этих колебаний определяется жесткостью закрепления тела, характеризующей связь между силой и смещением. Если сила связана со смещением по линейному закону
Fx = - kx (13)
(где k – некоторый коэффициент, определяемый свойствами рассматриваемой системы, называемый коэффициентом восстанавливающей (возвращающей) силы), то из сравнения (13) с выражением для силы при гармонических колебаниях (12) следует, что
k = m ω20 (14)
и циклическая частота гармонических колебаний
ω0 = 
, (15)
а период колебаний T = 
= 2π 
. (16)
Как видим, частота и период колебаний зависят только от свойств системы (жесткости закрепления тела около положения
Рис.1. Простое гармоническое колебание. А – амплитуда, Т - период
Рис.2. Один из вариантов нелинейной зависимости силы от смещения
 |
U(0) = 0 x
Рис.3. Смещение, возвращающая сила и начало отсчета потенциальной энергии
равновесия и от его массы), но не от амплитуды колебаний. Одно и то же тело, производя колебания с разной амплитудой, совершает их с одинаковой чистотой. Это очень важное свойство гармонических колебаний. Напротив, амплитуда колебаний А и начальная фаза α определяются не только свойствами колеблющейся системы, но и начальными условиями ее движения, т.е. начальным смещением из положения равновесия x0 = х(t = 0) и скоростью υ0= υ(t = 0). Из (1) и (7), получим
(17)
Решив систему уравнений (17) относительно А и α, находим
A = 
, α = - arctg 
. (18)
Заметим, что однозначное определение угла α (определение четверти, в которой он находится) производится с учетом (17)
Если систему каким-либо образом заставили совершать колебания (например, сместив из положения равновесия на х0 или сообщив начальную скорость v0) и предоставили самой себе, то возникающие колебания называют собственными колебаниями, а частоту колебаний – собственной частотой.
Используя выражение для возвращающей силы (13), нетрудно найти потенциальную энергию колеблющейся частицы. Будем считать, что потенциальная энергия U (x) равна нулю в положении равновесия x = 0 (нулевой уровень потенциальной энергии (рис. 3)). По определению потенциальной энергии она равна работе силы F (x) при перемещении частицы из смещенного положения x на нулевой уровень
Ux = A (F) (19)
Поскольку сила F (x) направлена к положению равновесия и линейно зависит от x, то ее работа при таком смещении будет положительной и равной
A = <F> (x – 0) = 
x = 
. (20)
Следовательно, потенциальная энергия гармонического осциллятора
U = , (21)
или, учитывая (15)
U = 
. (22)
Кинетическая энергия осциллятора
T =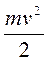 
(23)
Подставив (2) и (3) в (23) и (24), получим
U = 
cos2 (ω0 t + α) = 
(1 + cos 2(ω0 t + α)) (24)
T = sin2 (ω0 t + α) = (1 - cos 2(ω0 t + α)) (25)
т.е. и потенциальная, и кинетическая энергии частицы в процессе колебания изменяются со временем, причем таким образом, что когда одна из них увеличивается, другая – уменьшается. Колебания энергий происходят с удвоенной частотой колебаний осциллятора. Полная же энергия гармонического осциллятора
E = T + U = 
= const (26)
остается все время постоянной и равной максимальной кинетической энергии
Tmax = (27)
или, что то же самое, максимальной потенциальной энергии
Umax = 
(28)
Другими словами, процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Средние же (за период колебаний) значения потенциальной и кинетической энергий одинаковы и каждое из них равно 0,5E:
< T > = < U > = 0,5E. (29)
Математический маятник
В качестве примера гармонических колебаний рассмотрим малые колебания математического маятника - материальной точки массой m, подвешенной на невесомой и нерастяжимой нити длинной l в поле тяжести Земли. Когда маятник висит вертикально, сумма сил действующих на частицу (силы тяжести, действующая со стороны Земли, mg, и силы натяжения нити 
)
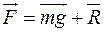= 0 (30)
т.е. частица массы m находится в равновесии.
Сместим частицу m из положения равновесия по дуге окружности радиуса l на величину
α = l θ, (31)
где θ – угол отклонения нити (в радианах) (рис.4а). При этом сила тяжести 
останется без изменений, в то время как сила натяжения нити 
изменяется не только по направлению, но и по величине, в итоге результирующая сила , действующая на частицу, станет отличной от нуля и будет направлена к положению равновесия (т.е. эта сила возвращающая, восстанавливающая, а положение равновесия устойчивое). Из рис. 4а видно, что
Fx = - mg sin θ (32)
или, используя (31),
Fx = - mg sin (x/l) (33)
Из (33) следует, что возвращающая сила Fx зависит от x по нелинейному закону. Следовательно, колебания математического маятника в общем случае не являются гармоническими. Однако, в случае малых колебаний, когда выполняется условие x << l, отношение x/l << 1 и и sin (x/l) 
tg (x/l) x/l. Поэтому при малых колебаниях возвращающая сила
Fx = - mg 
(34)
линейно зависит от x, причем коэффициент возвращающей силы
k = 
. (35)
Таким образом, при малых смещениях от положения равновесия математический маятник колеблется по гармоническому закону
x(t) = A cos(ω0t + α)
с частотой
ω0 = = 
(36)
и периодом
T = = 2π 
. (37)
Отметим, что длина маятника с периодом колебаний T0 = 1 с (для стандартного значения ускорения свободного падения вблизи поверхности Земли g0 = 9,81 м/с2) равна 24,8 см.
Если маятник находится в глубокой шахте на глубине h или на вершине горы высотой h (не на борту спутника), то его период колебаний будет определяться ускорением свободного падения в месте нахождения маятника. Если не учитывать вращение Земли и воспользоваться выражениями для g в шахте на глубине h, то получим, что на этой глубине
T = 2π 
(38)
(где T0 – его период колебаний на поверхности Земли и R3 – радиус Земли), а на высоте h
T = 2π 
> Т0 . (39)
Отметим, что в случае, когда глубина шахты h << R3, стоящий в (38) сомножитель 1/ 
можно приближенно заменить на (1 + h/2R3). В этом случае период колебаний маятника
T T0 
(40)
Рассмотрим теперь вопрос о том, как изменяется колебательное движение математического маятника, если на материальную точку, кроме силы тяжести, действует еще постоянная внешняя си
Рис.4а. Математический маятник и действующие на него силы
Рис.4б. Математический маятник под действием сторонней силы
ла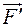 
(например, сила Архимеда, когда маятник движется в жид- кости).
В положении равновесия равнодействующая всех сил, действующих на частицу
= 0 (41)
Из (41), в частности, следует, что в положении равновесия векторы 
(вертикаль), (нить) и лежат в одной плоскости.
Соотношение (41) можно записать в виде
(42)
где
(43)
т.е. в этом случае нить маятника в положении равновесия не вертикальна, а расположена вдоль вектора 
. Обратим внимание, что условие равновесия (42) формально совпадает с (30) с той лишь разницей, что в (30) стоит , а в (42) - . Поэтому, все формулы, написанные после (30) и относящиеся к выражению периода колебания математического маятника, остаются в силе и в нашем случае, если в них заменить , на . Таким образом, при действии на маятник постоянной силы 
он будет совершать малые гармонические колебания около положения равновесия, в котором нить расположена вдоль вектора , с частотой
ω0 =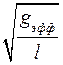 
(44)
и периодом
T = 2π 
, (45)
где
gэфф = 
(46)
- абсолютное значение (модуль) вектора .
Полученные выше результаты можно использовать при рассмотрении задачи о гармонических колебаниях математического маятника, когда его точка подвеса движется относительно Земли с постоянным ускорением 
. Для этого перейдем в неинерциальную систему отсчета, связанную с точкой подвеса. Как известно, закон движения материальной точки (второй закон Ньютона) в неинерциальной системе отсчета совпадает с законом движения ее в инерциальной системе отсчета, если считать, что на эту точку, кроме реальных сил, действует также фиктивная сила инерции 
. На основании этого можно заключить, что в случае, когда точка подвеса математического маятника движется с постоянным ускорением , маятник может совершать малые гармонические колебания около положения устойчивого равновесия, в котором нить маятника расположена вдоль вектора
= 
(47)
с частотой (44) и периодом (45), где
gэфф = 
.
Задача 1. Самолет стартует под углом α к горизонту с ускорением а (рис.5). Найти частоту малых колебаний математического маятника длины l,подвешенного в самолете.
Решение
Найдем эквивалентное ускорение g¢ обусловленное инерционными силами и силой тяжести (рис. 5). Из чертежа, используя теорему косинусов, имеем:
(g¢')2 = а2 + g2 + 2аg sin α. (48)
Далее используем соотношение ω2 = g1 /l.
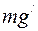
Рис. 5. Векторы сил и ускорений (к задаче 1)
Пружинный маятник
В качестве другого примера гармонического осциллятора рассмотрим пружинный маятник – материальную точку массой m, прикрепленную к одному концу идеальной невесомой пружины жесткостью к, другой конец которой закреплен. Длина пружины в нерастянутом положении равна 
.
Пусть на материальную точку массой m действует, кроме силы упругости пружины 
, постоянные силы 
, 
, …, не зависящие от удлинения пружины, ни от кинематических характеристик движения материальной точки (например, ее скорости). В положении равновесия
= 
,
т.е. пружина будет расположена вдоль равнодействующей силы и растянута (или сжата) на величину
Δl =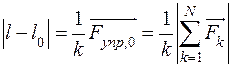 
. (49)
Если теперь вывести пружину из положения равновесия, растянув или сжав ее на величину x, отсчитываемую от положения равновесия, то равнодействующая сила не изменится, а сила упругости увеличится на величину kx. В результате этого появиться результирующая сила, направленная в сторону положения равновесия (возвращающая сила) и равная
Fx = - kx
Отсюда видно, что возвращающая сила линейно зависит от смещения x, причем коэффициент возвращающей силы равен жесткости пружины
k = к,
а это означает, что пружинный маятник будет совершать гармонические колебания с частотой
ω0 = (50)
и периодом
T = 2π
около положения равновесия, в котором пружина растянута на величину, определяемую выражением (49).
Обратим внимание, что собственная частота (и период) колебаний пружинного маятника определяется лишь жесткостью пружины и массой маятника и не зависит от внешних сил , , …, действующих на него, от которых зависит лишь растяжение пружины в положении равновесия. Поэтому, где бы ни находился пружинный маятник (в шахте, на вершине горы или на борту спутника) и как бы ни двигалась точка закрепления пружины, его частота и период колебаний будут всегда одними и теми же.
Коэффициент жесткости характеризует пружину в целом и зависит как от свойств материала, из которого она изготовлена, так и от ее геометрических характеристик. Некоторое представление об этих зависимостях можно получить на основании следующей модели. Заменим пружину стержнем длины L и сечения S. Пусть на стержень действует деформирующая (растягивающая или сжимающая) сила F. Она создает в стержне механическое напряжение σ = 
и удлиняет его на х. Относительное удлинение составляет ε = 
. Закон Гука представим в виде ε = 
. Здесь Е – модуль Юнга. Сравнивая с F = kx, получим k = 
. Жесткость пружины обратно пропорциональна ее длине.
2.1.4. Комбинированные осцилляторы
Комбинированный осциллятор - маятник, находящийся под воздействием нескольких сил различной физической природы, обеспечивающих возвращение отклоненного тела к одному и тому же положению устойчивого равновесия. Будем считать, что осциллятор совершает одномерные движения. Поэтому комбинацию математического маятника и пружинного маятника, показанную на рис. 6, рассматривать не будем, поскольку здесь меняются как угол отклонения, так и длина маятника. Это колебания с двумя степенями свободы.
Задача 2. Положительный заряд q сосредоточен на материальной точке массой m, которая подвешена в вакууме на невесомой нерастяжимой непроводящей нити длины l на высоте h над провод-
Рис.6. Математический маятник на упругом подвесе
ником (электропроводность которого бесконечна), занимающим нижнее полупространство. Граница раздела вакуума и металла – плоскость. Материальную точку отклоняют на малый угол от положения устойчивого равновесия. Найти собственную частоту колебаний такого комбинированного осциллятора.
Рис.7. Заряженная материальная точка, колеблющаяся над проводящим полупространством.
AB = BC = h; AD = Δh; l = ç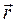 
ç- длина нити; 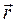- радиус-вектор, проведенный из точки О в точку Р.
Решение
На точку действуют сила тяжести, сила натяжения нити и сила электростатического (кулоновского) взаимодействия (рис. 7).
Рассмотрим подробнее силу кулоновского взаимодействия Fk.
Заряд +q перераспределяет свободные электроны проводника. В результате на поверхности раздела появляется отрицательный заряд по величине равный заряду q. Между исходным зарядом и наведенными зарядами возникает электростатическое взаимодействие. При колебаниях поверхностные заряды будут перемещаться, возникнут токи, что приведет к выделению джоулева тепла и магнитному взаимодействию. Однако, в хорошем металлическом проводнике (с бесконечной электропроводностью) при малых скоростях движения зарядов этими явлениями можно пренебречь.
Величину и направление кулоновской силы можно найти из сравнения картины силовых линий электрического диполя и картины силовых линий заряда, подвешенного над идеальным проводником. Силовые линии входят в проводник под прямым углом и их густота тем больше, чем ближе точка на поверхности проводника к точке B, лежащей на оси симметрии картины. Таким образом, картина силовых линий для рассматриваемого случая аналогична картине силовых линий диполя с расстоянием между положительным и отрицательным точечными зарядами равным 2h. Тогда Fk = 
для оси симметрии. Это поле неоднородно, но для малых колебаний момент кулоновской силы, как и момент силы тяжести можно считать пропорциональным углу α.
При отклонении нити на угол α материальная точка поднимается на высоту Δh = l(1 – cos α). Это приводит к изменению величины силы Fk:
Fk = 
.
Однако, при малых колебаниях, когда
<< 1 т.е. 
<< 1
силу кулоновского взаимодействия заданного заряда и наведенных поверхностных зарядов можно считать неизменной.
Момент инерции материальной точки (относительно оси вращения О параллельной поверхности идеального проводника) J0 = ml2, l – длина нити. Момент сил, действующих на материальную точку
N = (mg + Fk)lsinα. (51)
Здесь PD = l sinα - плечо действующих сил.
Связь между векторами скорости, угловой скорости и вектором 
направленным от центра вращения по радиусу к материальной точке задается соотношением:
= [ 
, 
]
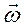Если скорость материальной точки направлена влево, то угловая скорость 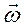и момент импульса 
= J0 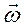направлены против момента сил 
. Поэтому основное уравнение динамики вращательного движения (уравнение моментов) запишется в виде
J0α" = - (mg + Fk) lsinα, (52)
где α" = ε =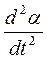 
угловое ускорение.
Тогда из (52) для sin α ≈α получаем
α" + 
l α = 0
В соответствии со стандартными обозначениями ω02 = , где ω0 собственная частота. Если бы заряда на материальной точке не было, то ω012 = mg/J0. Если бы можно было «отключить» силу тяжести, то ω022 = Fk/J0. Поэтому мы можем записать ω02 = ω012 + ω022. Если бы возвращающий момент обеспечивали n сил различной физической природы, то
ω02 = 
. (53)
Разумеется, это соотношение верно только для малых колебаний.
