,
где wi, – доля признака (в коэффициентах) в отдельных сериях; и общая доля признака во всей выборочной совокупности (
).
Среднюю ошибку выборки находят по формуле:
,
где R – общее число серий.
Пример 5. Для определения средней урожайности зерновых культур в области проведена серийная бесповторная выборка, в которую вошло пять районов из 40. Средняя урожайность по каждому отобранному району составила ц с га:
I район – 42, II район – 39, III район – 38, IV район – 41, V район – 40.
Определить с вероятностью 0,954 пределы, в которых будет находиться средняя урожайность зерновых культур по области.
Найдем общую выборочную среднюю. Она равна:
ц с га.
Определим межсерийную дисперсию:
Рассчитаем предельную ошибку серийного бесповторного отбора:
ц с га.
Следовательно, с вероятностью 0,954 можно утверждать, что средняя урожайность зерновых культур будет находиться в пределах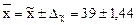 
ц с га.
Под типическим отбором понимается такой способ отбора, когда перед производством выборки генеральная совокупность делится на группы по какому-либо существенному (типическому) признаку, а затем из каждой группы производится случайный отбор единиц. Данные выборки затем распространяются на всю совокупность, а не на отдельные ее части.
Из всех типических групп можно отбирать некоторое число единиц непропорциональное численности самой группы, но можно и отбирать число единиц пропорциональное этой численности. Чаше всего на практике используют пропорциональный отбор:
.
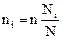Например, если из каждой группы будет отбираться 10% единиц, то получим пропорциональный типический отбор.
Разбивка на типические группы дает возможность избежать влияния межгрупповой вариации на точность выборки, т.к. в типическую выборку должны обязательно лопасть представители всех групп, что может не произойти при случайном отборе. Поэтому средняя ошибка типической выборки будет зависеть только от средней из групповых дисперсий, а не общей дисперсии, как это имеет место в случайной выборке.
Средняя ошибка пропорционального типического бесповторного отбора определяется по формуле:
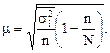
Формула же численности отбора аналогична формуле собственно-случайной выборки с той лишь разницей, что вместо общей дисперсии в ней фигурирует средняя из частных дисперсий.
Важное значение для теории н практики выборочного исследования имеет сочетание группового отбора с индивидуальным. Он связан со стадийностью, ступенчатостью отбора, когда формирование выборки происходит не сразу, а проходит несколько ступеней.
Ошибка многоступенчатого отбора в общем виде определяется по формуле:
,
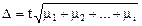где mi– средняя ошибка соответствующей ступени отбора.
Например, при двухступенчатом отборе первоначально отбираются группы единиц, а затем отбираются единицы из отобранных на первой ступени групп. Этот отбор называют иначе комбинированной выборкой. Ошибка этого отбора равна:
.
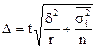