1. Определение средней арифметической интервалов ряда распределения.
Пример: Необходимо определить средний возраст студентов заочного отделения.
Таблица 4.2 Возраст студентов заочного отделения КубГУ
| Возраст студентов, лет (x) | Число студентов, f |  – середина интервала – середина интервала
|
| до 20 | ||
| 20–22 | ||
| 22–26 | ||
| 26–30 | ||
| 30–40 | ||
| Итого | 500 |

2. Определение общей средней из групповых средних.
При определении общей средней величины из групповых применяется формула для вычисления средней арифметической взвешенной, в которой в качестве вариантов (хi) принимаются группы, а в качестве частот – объем каждой группы.
Пример: определить среднюю урожайность зерновых культур по 3 группам совхозов.
Таблица 4.3 Урожайность зерновых по совхозам в 2009 г.
| Совхзы | xi – средняя урожайность, ц/га | Валовый сбор, ц (xifi) | Площадь посевов га, (f) |
| Итого | – | 720000 | 30000 |

3. Вычисление средней арифметической из относительных величин.
Применяется формула средней арифметической взвешенной, в которой вариантами являются относительные величины, а частотами – основания относительных величин.
Пример: определить средний процент выполнения плана по выпуску продукции по 3 предприятиям.
Таблица 4.4 – Выполнение плана по предприятиям отрасли
| № предприятия | % выполнения плана, хi | План выпуска продукции, тыс. р. (f) |
| Итого | – | 24900 |
 (4.3)
(4.3)
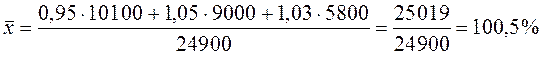
 (4.4)
(4.4)
.
Свойства средних величин
1. Если все варианты увеличить или уменьшить в несколько раз, то средняя арифметическая увеличится или уменьшится во столько же раз.
2. Если все варианты увеличить или уменьшить на одно и то же число, то средняя увеличится или уменьшится на то же число.
3. Средняя арифметическая суммы нескольких величин равна сумме средних арифметических этих величин.
4. Если все частоты увеличить или уменьшить в несколько раз, то средняя не изменится.
5. Алгебраическая сумма отклонений значений признака от средней арифметической всегда равна нулю.
Пример: имеется ряд распределения: 5, 10, 15, 20, 15.

Отклонения составят следующие значения: –8, –3, 2, 7, 2.
Сумма отклонений от средней величины равна нулю:

Свойства средней арифметической применяются для упрощения ее расчетов.
Пример: определить средний размер вклада.
Таблица 4.5 – Вспомогательная таблица для расчета среднего размера вклада способом моментов
| Размер вклада р. (х) | Число вкладов, (f) | 
| x'–A* (A = 450) |  = x"
i = 100** = x"
i = 100**
| f'= | 
|
| 200–300 | – 200 | – 2 | – 10 | |||
| 300–400 | – 100 | – 1 | – 6 | |||
| 400–500 | ||||||
| 500–600 | ||||||
| 600–700 | 5 | |||||
| Итого | 230 | – | – | – | 23 | –3 |


Данный способ расчета средней арифметической взвешенной называется способом моментов (или способом расчета от условного нуля).






