В результате систематизации и обработки первичных материалов статистического наблюдения получают упорядоченные ряды цифровых показателей, характеризующих либо изменение размера явления во времени (ряд динамики, о котором будет идти речь в теме «Ряды динамики»), либо распределение единиц совокупности по тем или иным варьирующим признакам в статике (ряд распределения).
Ряд распределения - это ряд цифровых показателей, представляющих собой распределение единиц совокупности по одному признаку, разновидности которого расположены в определенной последовательности.
Элементами ряда распределения являются: варианты и частоты.
Вариантами ( 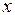 ) называются отдельные значения группировочного признака, которые он принимает в вариационном ряду. Варианты могут выражаться числами положительными и отрицательными, абсолютными и относительными. Числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения, называются частотами (
) называются отдельные значения группировочного признака, которые он принимает в вариационном ряду. Варианты могут выражаться числами положительными и отрицательными, абсолютными и относительными. Числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения, называются частотами (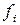 ). Численность единиц в каждой группе может быть выражена не только численностью единиц (частотами), но и в долях (процентах) от общей численности единиц совокупности (частостями). Сумма частостей равна 1, если они выражены в долях единицы, и 100%, если они выражены в процентах.
). Численность единиц в каждой группе может быть выражена не только численностью единиц (частотами), но и в долях (процентах) от общей численности единиц совокупности (частостями). Сумма частостей равна 1, если они выражены в долях единицы, и 100%, если они выражены в процентах.
В зависимости от статистической природы вариантов различают два вида рядов распределения: атрибутивные и вариационные.
Ряды, построенные по качественному признаку, называют атрибутивными (например, распределение населения по полу, распределение предприятий по форме собственности и др.).
Ряды распределения по количественному признаку называют вариационными (распределение населения по размеру дохода, распределение банков по размеру активов).
Так как вариация признака может быть дискретной (прерывной) и непрерывной, то различают вариационные ряды дискретные и непрерывные (интервальные). В дискретный вариационных рядах значения вариантов выражаются целыми числами и отличаются друг от друга на вполне определенную величину (одну или несколько единиц). Примерами дискретных вариационных рядов являются: распределение семей по числу детей, распределение квартир по числу комнат и т.д.
При непрерывной вариации признака его величина может принимать как целые, так и дробные значения, то есть любые значения в определенном интервале (возраст, стаж работы, прибыль и т.д.). Для рядов распределения с равными интервалами частоты дают представление о степени заполненности интервала единицами совокупности. Для рядов распределения с неравными интервалами в целях сравнения заполнености интервалов рассчитывается плотность распределения, то есть число единиц совокупности (частота, частость), приходящееся в среднем на единицу ширины интервала. Плотность распределения может быть абсолютной (отношение частоты к ширине интервала) и относительной (отношение частости к ширине интервала).
Ряды распределения могут строиться по накопленным частотам (частостям), которые показывают, какое число единиц имеют величину варианта, не большую данной. Такие ряды распределения называют кумулятивными.
Для изображения рядов распределения применяются различные графики.
Так, распределение населения региона по месту жительства может быть изображено с помощью секторной диаграммы (рис. 5.1).
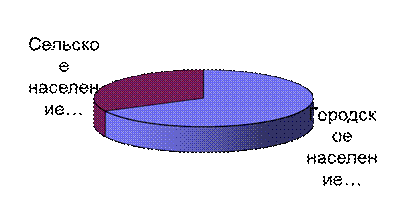
Рис. 5.1. Распределение населения региона по месту
жительства на 1 января 2001г.
Для изображения вариационных рядов применяются линейные и плоскостные диаграммы, построенные в прямоугольной системе координат.
Дискретные вариационные ряды, варианты у которых выражаются целыми числами, изображаются в виде полигона распределения. Полигон распределения представляет собой замкнутый многоугольник, абсциссами вершин которого являются значения варьирующего признака, а ординатами - соответствующие им частоты или частости (рис. 5.2).
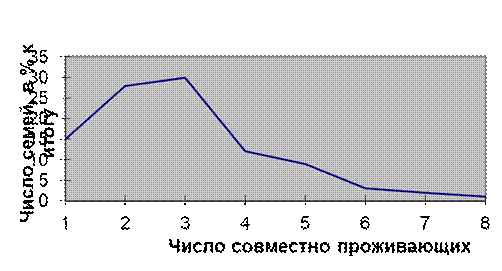
Рис.5.2. Распределение одиночек и семей города по числу совместно
проживающих.
Графическое изображение непрерывных вариационных рядов осуществляется с помощью так называемой гистограммы. Для построения гистограммы на оси абсцисс в соответствии с принятым масштабом откладывают границы интервалов, на которых строятся прямоугольники. Высоты этих прямоугольников пропорциональны плотностям распределения соответствующих интервалов. На рис. 4.3 изображена гистограмма распределения населения региона по размеру среднедушевого совокупного дохода в месяц в 2000г. 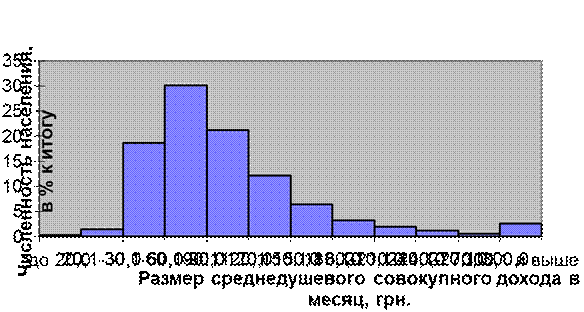
Рис.5.3. Распределение населения региона по размеру среднедушевого
совокупного дохода в месяц в 2000г. (по данным бюджетных
обследований семей).
При неравных интервалах гистограмма строится только по плотности распределения.
Для графического изображения вариационных рядов используется также кумулятивная кривая (кумулята). Для ее построения на оси абсцисс откладывается значение дискретного признака (или границы интервала), а на оси ординат - нарастающие итоги частот или частостей, соответствующие этим значениям признака (или верхним границам интервала). Кумулята распределения населения региона по размеру среднедушевого совокупного дохода в месяц приведена на рис.5.4.
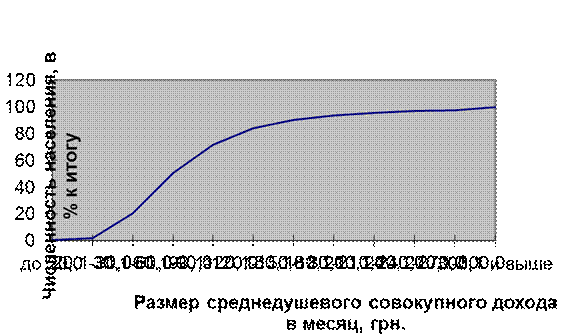
Рис.5.4. Кумулята распределения населения региона по размеру
среднедушевого совокупного дохода в месяц в 2000г.
(по данным бюджетных обследований семей).
С помощью кумулятивных кривых можно графически изображать процесс концентрации. Для графического изображения явления концентрации используются нарастающие итоги показателей. Для этого нужно иметь в групповой таблице кроме сумм накопленных частостей также суммы накопленных значений важнейших признаков (группировочного в первую очередь), выраженных в процентах к итогу. На оси абсцисс откладывают нарастающие итоги частостей, а соответствующие нарастающие итоги показателей - на оси ординат. Соединив отрезками прямых найденные таким образом точки, получают ломаные линии, которые называют кривыми концентрации.






