Я в душе не ебу!
28.) Вариация-это…
различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. Причиной возникновения вариации являются различные условия существования разных единиц совокупности.
Главное значение средних величин.
Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений варьирующего признака.
30.) Среднее арифметическое-это…
сре́днее арифмети́ческое — одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений, деленную на их количество.
31.) Формула простой средней арифметической.
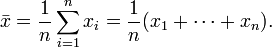
32.) Формула взвешенной средней арифметической.
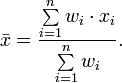
Категории средних величин и виды средних, к которым они относятся.
степенные средние (средняя гармоническая, средняя геометрическая, средняя арифметическая и др.). Для вычисления степенных средних необходимо использовать все имеющиеся значения признака. Если рассчитывать все виды степенных средних для одних и тех же данных, то их значения окажутся одинаковыми. Тогда действует правило мажорантности средних: с увеличением показателя степени средних увеличивается и сама средняя величина.
структурные средние (мода, медиана). Мода и медиана определяются лишь структурой распределения. Поэтому их именуют "структурными позиционными средними". Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.
Форума степенной средней степени d.
35.) Формула средней квадратической. Статистический показатель на ее основе.
На основе данной формулы строится такой статистический показатель как дисперсия.
36.
Формула средней кубической величины применяется при расчете с величинами кубических функций и исчисляется по формуле:
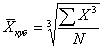(простая)
Х - индивидуальное значение.
N – число единиц изучаемой совокупности.
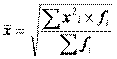(взвешенная)
fi – частота ряда распределения или удельный вес в совокупности.
37.
Средняя геометрическая величина дает возможность сохранять в неизменном виде не сумму, а произведение индивидуальных значений данной величины. Ее можно определить по следующей формуле:
Средние геометрические величины наиболее часто используются при анализе темпов роста экономических показателей.
Геометрическая простая
Для расчетов средней геометрической простой используется формула:
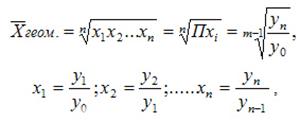
где:
§ 
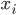— цепной коэффициент роста
§ 
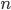— число этих коэффициентов роста
§ П — знак произведения
§ 
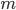— количество уровней ряда
§ 
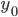— значение начального уровня ряда
§ 
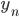— значение конечного уровня ряда
Геометрическая взвешенная
Для определения средней геометрической взвешенной применяется формула:
38.
Правило мажорантности средних:
Правило мажорантности средних: чем выше показатель степени m, тем больше величина средней.
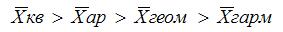
39.Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.
Средняя всегда обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. В отличие от средней абсолютная величина, характеризующая уровень признака отдельной единицы совокупности, не позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям. Так, если нужно сопоставить уровни оплаты труда работников на двух предприятиях, то нельзя сравнивать по данному признаку двух работников разных предприятий. Оплата труда выбранных для сравнения работников может быть не типичной для этих предприятий. Если же сравнивать размеры фондов оплаты труда на рассматриваемых предприятиях, то не учитывается численность работающих и, следовательно, нельзя определить, где уровень оплаты труда выше. В конечном итоге сравнить можно лишь средние показатели, т.е. сколько в среднем получает один работник на каждом предприятии. Таким образом, возникает необходимость расчета средней величины как обобщающей характеристики совокупности.
Вычисление среднего – один из распространенных приемов обобщения; средний показатель отрицает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей.
Для того, чтобы средний показатель был действительно типизирующим, он должен рассчитываться с учетом определенных принципов.
Остановимся на некоторых общих принципах применения средних величин.
1. Средняя должна определяться для совокупностей, состоящих из качественно однородных единиц.
2. Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц.
3. Средняя должна рассчитываться для совокупности, единицы которой находятся в нормальном, естественном состоянии.
4. Средняя должна вычисляться с учетом экономического содержания исследуемого показателя.
40.Ряд распределния является одним из видов группировок.
Ряд распределения — представляет собой упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака и подсчет числа единиц с одним и тем же значением признака.
В зависимости от признака, положенного в основу образования ряда распределения различают атрибутивные и вариационные ряды распределения:
Атрибутивными — называют ряды распределения, построенные по качественным признакам.
Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называются вариационными.
Формы вариционного ряда:
Ранжированный ряд – это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.
Дискретный ряд – представляет собой таблицу, состоящую из двух граф или строк: конкретных значений признака и числа единиц совокупности
Интервальный ряд – представляет собой таблицу,состоящую из двух граф или строк: интервалов признака, вариация которого изучается, и числа единиц совокупности,попадающих в данный интервал(частот), или долей этого числа от общей численности совокупности(частостей)
42.
Частота – численности отдельных вариант или каждой группы вариационного ряда n-i
43.
Накопленные частоты (обозначаются S) показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое, и определяются последовательным суммированием частот интервалов. При построении кумуляты интервального ряда распределения нижней границе первого интервала соответствует частота, равная нулю, а верхней границе — частота данного интервала.
44.
Частость - частота, выраженная в долях единицы или в процентах к итогу.
45.
F - критерий Фишера является параметричесикм критерием и используется для сравнения дисперсий двух вариационных рядов. Эмпирическое значение критерия вычисляется по формуле:
где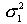 
- большая дисперсия, 
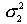- меньшая дисперсия рассматриваемых вариационных рядов.
Если вычисленное значение критерия Fэмп больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными. Иными словами, проверяется гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: H0={Dx=Dy}.
Критическое значение критерия Фишера следует определять по специальной таблице, исходя из уровня значимости α и степеней свободы числителя (n1-1) и знаменателя (n2-1).
Проиллюстрируем применение критерия Фишера на следующем примере. Дисперсия такого показателя, как стрессоустойчивость для учителей составила 6,17 (n1=32), а для менеджеров 4,41 (n2=33). Определим, можно ли считать уровень дисперсий примерно одинаковым для данных выборок на уровне значимости 0,05.
Для ответа на поставленный вопрос определим эмпирическое значение критерия: 
При этом критическое значение критерия Fкр(0,05;31;32)=2.
Таким образом, Fэмп=1,4<2=Fкр, поэтому нулевая гипотеза о равенстве генеральных дисперсий на уровне значимости 0,05 принимается.
46.
