Понятие о дифракции волн. Принцип Гюйгенса

Как уже отмечалось, у пругие колебания в среде передаются по эстафетному механизму от одной ее точки к соседним точкам. Эта особенность распространения волн положена в основу принципа, предложенного Х. Гюйгенсом. Согласно этому принципу каждая

точка фронта волны Ф (t) в момент времени t рассматривается как самостоятельный источник элементарных сферических вторичных волн. Огибающая этих вторичных волн дает фронт волны Ф (t + Δ t) в последующий момент времени t + Δ t (рис. 9.). В однородной изотропной среде волновые фронты вторичных волн имеют вид сфер радиуса v Δ t, центры которых лежат на поверхности Ф (t) В такой среде фронт плоской (рис. 9.) или сферической (рис. 9.) волн, перемещаясь со скоростью v, всегда остается геоме-

Рис. 9.

трически подобным себе. При этом огибающую нужно строить только по ту сторону от волнового фронта Ф (t), в которую распространяется рассматриваемая волна.

Принцип Гюйгенса является чисто геометрическим способом построения волновых фронтов

Если на пути волны расположено какое-либо препятствие, например, экран (рис. 9), то вторичные волны, распространяющиеся вблизи его краев, будут заходить (загибаться) за экран. В результате и фронт результирующей волны (огибающая вторичных волн) у краев экрана загибается, а лучи меняют свое направление и заходят туда, куда при прямолиней-

Рис. 9.

ном распространении волны они заходить не должны (в область геометрической тени).

Отклонение волн от прямолинейного направления распространения и захождение в область геометрической тени называется дифракцией волн. Дифракция существенно зависит от соотношения между размерами отверстий или экранов препятствий) и длиной волны. Если размер экрана или отверстия в экране во много раз больше длины волны, то за экраном получится тень с ясно выраженными границами, так как интенсивность волн, отклонившихся в область тени, ничтожно мала по сравнению с интенсивностью не отклонившихся волн (рис. 9.). Дифракция в этом случае незаметно. Если же размер препятствия или отверстия сравним с длиной волны, дифракция будет наблюдаться более отчетливо (рис. 9.).

Пользуясь принципом Гюйгенса, можно получить законы отражения волн от границы раздела двух сред и преломления волн при переходе из одной среды в другую.

 

 

 

Рис.9.

 

Пусть на плоскую границу MN раздела двух сред 1 и 2 падает плоская волна, распространяющаяся вдоль направления KA. Угол i между KA и перпендикуляром AE к плоскости MN называется углом падения. Плоскость AB – фронт падающей волны. В изображенной на рисунке момент фронт волны достиг отражающей поверхности в точке A. Следовательно, эта точка начинает испускать вторичную волну. За время Δ t = BC / v прохождения падающей волной расстояния BC фронт вторичной волны, распространяющейся в первой среде, достигает точек полусферы, радиус AD которой равен v Δ t = BC. Положение фронта отраженной волны в этот момент в соответствии с принципом Гюйгенса изобразится плоскостью CD, а направление распространения этой волны – лучом AD. Угол i′ между нормалью AE и лучом называется углом отражения. Из равенства треугольников ABC и ADC следует закон отражения волн: угол отражения i′ равен углу падения i.

Аналогичным образом выводится и закон преломления волн при переходе из одной среды в другую (рис. 9.). Пусть скорость распространения волны в первой среде v ₁, а во второй v ₂. Тогда за время Δ t = BC / v ₂ падающей волной расстояния BC в первой среде фронт вторичной волны, возбуждаемой во второй среде точкой А достигнет точек полусферы, радиус которой AD = v ₂Δt = BC.

 

Рис. 9

 

В соответствии с принципом Гюйгенса фронт результирующей преломленной волны, распространяющейся во второй среде, изображается плоскостью CD, а направление ее распространения – лучом AD. Угол r между лучом AD и продолжением нормали AE называется углом преломления. Из прямоугольных треугольников ABC и ADE следует, что BC = AC sin i и AD = AC sin r, или

 

Мы получили закон преломления волн: отношение синуса угла падения к синусу угла преломления равно отношению фазовой скорости волны в первой среде к фазовой скорости волны во второй среде.

Величина = называется относительным показателем преломления второй среды по отношению к первой. Таким образом, из принципа Гюйгенса вытекает, что

Следует подчеркнуть, что все полученные выше закономерности справедливы только для изотропных сред, в которых скорости волн не зависят от направления распространения. В противном случае вторичные волны не будут сферическими.

 

 

Звуковые волны

 

Механические колебания в определенном интервале частот, распространяющиеся в упругой среде, называются звуковыми колебаниями или просто звуками, а учение о звуках – акустикой. Звуковые волны с частотой от 16 до 20 000 Гц называются собственно звуками. Эти волны воздействуют на органы слуха человека, вызывая ощущение звука. Упругие волны с частотой больше 20 000 Гц называются ультразвуком, а с частотой ниже 16 Гц – инфразвуком. Эти волны не вызывают звуковых ощущений. К звуковым волнам применимы все рассмотренные выше общие закономерности колебательного и волнового механического движения в упругих средах. Если известны формула звуковой волны и ее скорость, можно определить смещение и характер колебаний всех точек объема среды, охваченного волновым движением. Область среды, находящейся в состоянии звукового волнового движения, называется звуковым полем.

Скорость распространения продольной волны в сплошной среде (твердой, жидкой и газообразной) определяется по формуле (9.7), которую для общего случая можно записать в виде

 

где – модуль упругости, соответствующий определенному типу деформации рассматриваемой среды. Скорость звуковой волны v (или просто – скорость звука) зависит от физических свойств среды, в которой она распространяется, частота волны и ее период Т от свойств среды не зависят, а задаются источником волн, следовательно, длина волны также зависит от свойств среды. Скорость звука в воздухе, как будет показано в разделе «Молекулярная физика», составляет около 330 Поэтому собственно звуковому диапазону соответствуют в воздухе длины волн от 20 м до 2 см. Ультразвуковому диапазону соответствуют частоты до 10⁹ Гц а длины волн от 2 см до 0,5 мкм.

 

 

Рис. 9

 

Гармонические колебания определенной частоты воспринимаются нами как определенный тон, называемый простым или чистым тоном. Чисто гармонические монохроматические звуковые волны звучат «бесцветно» и монотонно. Реальные источники звука излучают обычно не гармоническую волну, а совокупность конечного или бесконечного числа гармонических волн с различными частотами и амплитудами. Эта совокупность частот колебаний, составляющих данный звук, называется его акустическим спектром. Для наглядного представления акустического спектра звука пользуются его графическим изображением. При этом по оси абсцисс откладывают значение частот, а по оси ординат – интенсивность звуковых волн с этими частотами. Звуки, акустический спектр которых состоит из отдельных частот (изображается в виде отдельных вертикальных линий – линейчатый спектр, рис. 9., а), называются тональными или музыкальными. Звуки, спектр которых состоит из частот почти непрерывно заполняющих определенный интервал частот (сплошной спектр), называются шумами. Акустический спектр шума показан на рис. 9., б, где dI – интенсивность волн с частотам, заключенными в интервале от до

В музыкальном звуке из всех частот спектра особо выделяются колебания с наименьшей частотой (основной тон). Они имеют наибольшую амплитуду, а значит, и интенсивность по отношению к высшим гармоникам (колебаний с большими частотами, называемыми обертонами)

При субъективном восприятии звуки различают по высоте, тембру и громкости. Каждой такой физиологической характеристике восприятия звука соответствует физическая его характеристика. Высота звука определяется частотой основного тона: чем больше его частота, тем больше высота тона воспринимаемого звука. Малые частоты колебаний вызывают ощущение так называемого низкого тона (бас, баритон); большие частоты колебаний вызывают ощущение звука высокого тона (сопрано, дискант).

Тембр звука (его окраска) определяется количеством обертонов и отношением их амплитуд к амплитуде основного тона. На тембр звука оказывает влияние характер увеличения амплитуды на начальном участке звучания и характер ее уменьшения в конце звучания.

Различие в начальных фазах обертонов на тембр звука влияния не оказывает. Объясняется это тем, что сила возбуждения отдельных нервных волокон, обеспечивающих восприятие тонов, зависит только от амплитуды (интенсивности) обертонов и не зависит от фазы их колебаний. Чем сложнее спектр звука, чем больше в нем обертонов и чем ближе их амплитуда к амплитуде основного тона, тем богаче, красивее тембр звука в музыкальном отношении. Различный спектральный состав звуков, возбуждаемых разными музыкальными инструментами, позволяет отличить на слух, например, флейту от скрипки или рояля.

Несколько одновременно приходящих звуковых колебаний, частоты которых находятся в определенном соответствии, создают впечатление созвучия, приятного (консонанс) или неприятного (диссонанс). Большое число одновременных звуковых колебаний с самыми различными частотами создают впечатление шума.

Распространяясь в пространстве, звуковые волны переносят энергию (см. п. 7.3). Для звукового диапазона интенсивность волны называют также силой звука и обозначают той же буквой I.

Человеческое ухо воспринимает звуки, сила которых заключена в определенных пределах. Наименьшее значение силы воспринимаемых звуков называется порогом слышимости. Величина этого порога зависит от частоты звуков Наиболее чувствительно ухо человека к звукам частотой от 1000 до 4000 Гц. Для частоты 3000 Гц порог слышимости примерно равен 10^–12 Вт/м². При силе звука порядка 1–10 Вт/м² звуковая волна перестает восприниматься как звук. Такой звук воспринимается как давление и боль в ухе. Отсюда следует, что звуки, воспринимаемые ухом, различаются по силе примерно в 10¹²–10¹³ раз.

Интенсивность (сила) звука определяет его громкость. Однако субъективно оцениваемая громкость возрастает гораздо медленнее, чем интенсивность звуковых волн. Это связано с тем, что наше ухо, способное воспринимать звуки, отличающиеся по силе в 10¹³ раз, не нечувствительно к малым изменениям силы звука и замечает прирост громкости звука при увеличении силы последнего не менее, чем на 10–20%. При возрастании интенсивности в геометрической прогрессии громкость возрастает приблизительно в арифметической прогрессии, т.е. линейно. Поэтому для сравнения силы звуков пользуются не линейной, а логарифмической шкалой. Для этого вводится уровень громкости (силы) звука L, определяемый как

 

где – условно принятый за основу уровень интенсивности, равный порогу слышимости человеческого уха при частоте 3 кГц. Единица измерения громкости звука по логарифмической шкале называется белом (Б). На практике используется единица в 10 раз меньшая, которая называется децибелом (дБ). Уровень громкости в децибелах определяется по формуле

 

Весь диапазон воспринимаемых ухом звуков находится по уровню громкости в пределах от 0 (при I = I ₀) до 130 дБ (при I = 10 Вт/м²). Для справки укажем, что средний уровень громкости речи составляет 60 дБ, тиканье часов, производит шум в 20 дБ, а мотор самолета на расстоянии 5 м производит шум в 120 дБ. Средняя мощность, развиваемая человеком при разговоре, очень мала и составляет около 10^–5 Вт.

Звуковую волнуможно характеризовать величиной, называемой звуковым давлением, под которым понимают отклонение давления газа от его статического значения. Для плоской волны, распространяющейся вдоль положительного направления оси X, эта величина будет периодической функцией координаты x и времени t: p = p (x, t). Найдем явный вид этой функции. Пусть колебания звукового давления в плоскости x = 0, где располагается источник звука, происходят по закону

 

 

где – амплитуда колебаний звукового давления, – круговая частота колебаний, – начальная фаза. Эти колебания звукового давления будут распространяться вдоль оси X со скоростью v. В плоскость x они переместятся спустя промежуток времени Следовательно, начало колебаний звукового давления в плоскости x будут отставать от начала колебаний в плоскости x = 0 на промежуток времени τ и, следовательно, будет описываться соотношением

 

Это есть формула плоской гармонической звуковой волны. Здесь k = 2 𝜋 / 𝜆 – волновое число, 𝜆 – длина звуковой волны.

Эффект Доплера

 

Рассмотрим плоскую монохроматическую звуковую волну

 

 

распространяющуюся в газовой или жидкой среде вдоль оси X со скоростью . Представим себе, что вдоль этого направления равномерно движется наблюдатель (приемник звука) со скоростью v _п. Подставим в выражение волны вместо x путь, пройденный наблюдателем за время t, т.е. x = v _п t + x ₀, где x ₀ – значение x при t = 0. В результате получим

где Это выражение показывает, что для равномерно движущегося наблюдателя звуковая волна будет по-прежнему гармонической, но воспринимаемая им частота будет отличаться от частоты звука в системе, связанной со средой, а именно, она будет равна

Таким образом, частота, воспринимаемая удаляющимся от источника за наблюдателем, будет меньше частоты источника. При = частота обращается в нуль, а при > она становится отрицательной. Это значит, что слышимый наблюдателем звук будет в действительности доходить до него в обратном порядке, т.е. звук, излученный в более поздние моменты времени, дойдут до наблюдателя раньше, чем звук, излученный в более ранние моменты.

Если наблюдатель будет двигаться не от источника, а к источнику, то воспринимаемая им частота будет равна

 

где – скорость наблюдателя (приемника).

Изменение частоты звука при переходе от одной системы отсчета к другой носит общее название эффекта Доплера.

Выясним теперь, как влияет на изменение частоты движение источника звука. Предположим, что наблюдатель неподвижен, а источник звука движется со скоростью в направлении, противоположном направлению распространения звука, т.е. от наблюдателя. Обозначим воспринимаемую наблюдателем частоту через Чтобы определить ее, представим себе, что наблюдатель начинает двигаться по направлению к источнику со скоростью . Тогда воспринимаемая им частота не будет отличаться от ω. С другой стороны, она равна Поэтому

 

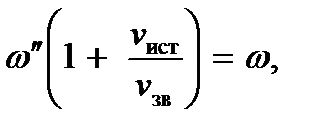
откуда

 

Она больше, чем ω.

Из полученных формул можно заключить, что если движутся и источник, и приемник, то воспринимаемая им частота будет

 

гд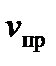е и – скорости приемника и источника звука, ω – частота звука при неподвижном источнике и неподвижной среде. Верхние знаки в этой формуле перед скоростями и берутся в том случае, когда векторы скорости приемника и источника направлены в сторону сближения. Если векторы скоростей v _пр и v _ист направлены в сторону удаления, следует брать нижние знаки перед соответствующей скоростью