Все волновые процессы, с которыми приходится иметь дело на практике, никогда не бывают строго гармоническими плоскими волнами. Однако любую реальную волну можно представить как суперпозицию плоских монохроматических волн, частоты и волновые числа которых заполняют интервал шириной ∆ ω и ∆ k соответственно. Эти интервалы могут быть и бесконечными. Если частоты (и волновые числа) компонент мало отличаются друг от друга и сгруппированы вблизи некоторой центральной частоты ω 0 (и волнового числа k 0, ∆ ω << ω 0, ∆ k << k 0), то такую суперпозицию называют группой волн, или волновым пакетом. Волновой пакет – это волна, которая отлична от нуля лишь в некотором интервале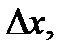 
а во всех других точках пространства равна нулю.
При распространении группы волн результирующее колебание в какой-либо точке x в момент времени t зависит от соотношения их фаз φ = kx – ωt, поэтому в одних точках волны вследствие интерференции будут усиливать друг друга, а в других ослаблять. В одних точках это усиление или ослабление будет меньше, в других больше. Если эти фазы будут взаимно почти противоположны, результирующее колебание будет мало. Но если в какой-либо точке x 0 в момент времени t фазы отдельных составляющих почти совпадут, то в результате интерференции в этой точке колебания сложатся и дадут результирующее колебание с максимальной амплитудой. Точку x 0, в которой амплитуда группы волн имеет максимальное значение, называется центром группы или центром волнового пакета.
Из того, что в центре группы фазы колебаний, вызываемых волнами различных, но близких часто и волновых чисел, совпадают следует, что в центре группы фаза колебаний не зависит от частоты и волнового числа, т.е. от того, какой из волн группы приписывается эта фаза. Математически это можно выразить в утверждении, что в центре группы производная фазы по волновому числу (или частоте) как производная постоянной равна нулю:
(7.16)
откуда
(7.17)
Мы видим, что положение центра группы, определяемой координатой x0, изменяется во времени, т.е. центр группы перемещается в пространстве равномерно со скоростью
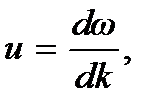(7.18)
где индекс «0», указывающий на то, что производная берется в центре группы, отброшен за ненадобностью.
Скорость, определяемая равенством (7.18), называется групповой скоростью, в отличие от введенной выше фазовой скорости 
являющейся скоростью переноса в пространстве любого значения фазы волны. Понятие фазовой скорости относится к плоской гармонической волне. Но реальные волны не являются плоскими гармоническими. Поэтому на практике обычно имеют дело с волновыми пакетами, а значит, и с групповой скоростью.
Наибольшее абсолютное значение результирующей амплитуды, как было установлено выше, получается в том случае, когда фаза φ остается почти постоянной в интервале волновых чисел от 
до 
Изменение фазы считается малым, пока оно не достигнет значения порядка π. Отсюда имеем условие того, чтобы амплитуда в указанном интервале имела большую абсолютную величину: 
Пусть изменение фазы на π достигается в точке x 1, тогда с учетом соотношений (7.16) и (7.17) получим
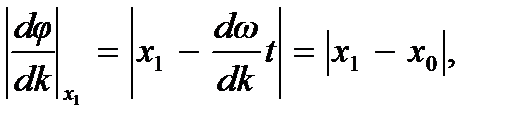
а значит, можно записать: 
Принимая величину 
за ширину волнового пакета, получим
(6.19)
Это соотношение показывает, что волна, волновые числа составляющих гармоник которой занимают спектральный интервал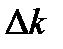 
конечной ширины, оказывается практически локализованным в области шириной 
(отсюда и название – волновой пакет). Эта область будет тем уже, чем шире интервал волновых чисел волн, образующих волновой пакет. С другой стороны, при стремлении 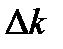к нулю (что имеет место в случае гармонической волны) ширина пакета стремится к бесконечности – волна занимает все бесконечное пространство и описывается гармонической функцией косинуса или синуса.
Соотношение (6.19) называют соотношением неопределенностей для волн (неопределенностями называют величины и 
). Другим соотношением неопределенностей для волн является соотношение
(7.20)
Это соотношение можно получить путем следующих рассуждений. Пакет шириной перемещается вдоль оси X со скоростью u, однако момент прохождения им заданной точки на оси X не может быть указан точно: неопределенность в определении этого момента оказывается порядка 
Волновой пакет характеризуется размытостью по волновым числам 
и частотам 
причем
Из этих двух приближенных равенств находим, что 
Тогда, используя соотношение (7.19), приходим к соотношению (7.20).
