В предыдущем параграфе мы рассмотрели образование стоячих волн в струне при наложении двух плоских волн, бегущих в противоположных направлениях, отражающихся на концах струны и снова бегущих навстречу друг другу. Такая стоячая волна будет существовать только в том случае, если на длине струны укладывается целое число полуволн. Стоячие волны при наложении двух бегущих волн – падающей и отраженной - могут наблюдаться и при многократных отражениях в любом замкнутом с обеих сторон участке пространства. В отсутствие затухания колебаний частиц, стоячая волна будет существовать здесь неограниченно долго, не меняя своего вида. Чтобы стоячая волна не меняла с течением времени своего вида, на границах участка должно удовлетворяться условие, установленное в предыдущем параграфе для узлов закрепленной или пучностей незакрепленной струны, т.е. условие 
Если левая граница находится в точке 
а правая – в точке 
то 
.
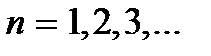Таким образом, в замкнутом с обеих сторон участке пространства могут существовать стоячие волны, не меняющиеся с течением времени, без постороннего источника, возбуждающего эти волны. Такая стоячая волна будет существовать только в том случае, если в интервале между границами среды укладывается целое число полуволн. Условие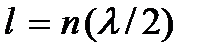 
можно записать также в виде 
Стоячие волны могут существовать и в замкнутом объеме среды, например, в закрепленном на одном конце или посередине упругого стержня. Если в таком объеме распространяются плоские волны, то условие образования стоячих волн тоже определяется некоторой совокупностью целых чисел. Рассмотрим простейший случай, когда ограниченный объем имеет форму куба со стороной l; три взаимно перпендикулярных ребра куба направим вдоль координатных осей X, Y, Z. Если стенки куба являются отражающими, то волновое поле в нем может существовать только в виде суперпозиции прямых и отраженных волн, т.е. в виде стоячих волн, имеющих узлы на гранях куба. Условия образования стоячих волн вдоль ребер куба (координатных осей) запишутся подобно условию образования стоячих волн в замкнутом с обеих сторон участке пространства. Учитывая это, получим, что для стоячей волны, являющейся суперпозицией прямой и отраженной волн, распространяющихся в объеме куба в произвольном направлении, задаваемым волновым вектором k, должны выполняться условия
(7.14)
где nx, ny, nz – целые положительные числа, нумерующие волны. Отсюда следует, что тройка целых чисел nx, ny, nz определяет один волновой вектор k с компонентами kx, ky, kz и одну стоячую волну. Общее число стоячих волн бесконечно. Величины kx, ky, kz можно трактовать как декартовы компоненты волнового вектора k.
Найдем число стоячих волн в кубе, модуль волнового вектора k которых лежит в интервале между k и k + dk, независимо от направления вектора k. Будем рассматривать величины kx, ky, kz как прямоугольные координаты точки трехмерного пространства волнового вектора k (k -пространства). Каждая такая точка представляет в k -пространстве одну стоячую волну. Поскольку, однако, промежутки 
между последовательными значениями волновых чисел (им соответствует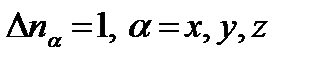 
), как видно из (6.10), одинаковы и равны 
, то каждой стоячей волне (одному типу колебаний) в этом k -пространстве будет соответствовать не одна точка, а целая ячейка в виде кубика со стороной и объемом 
Все k -пространство, таким образом, разделяется на кубические ячейки указанных размеров.
Соотношение
,
определяющее связь между модулем вектора k и его компонентами kx, ky, kz, в k -пространстве представляет собой сферу радиуса k. Поэтому все кубики, соответствующие стоячим волнам с указанным значением модуля волнового вектора, будут лежать в объеме шарового слоя радиусом k и толщиной dk. Этот объем равен 
Поскольку величины kx, ky, kz, как видно из (6.10), положительные, то следует рассматривать не весь указанный объем, а его часть, соответствующую первому положительному октанту, что составляет 1/8 часть всего объема слоя. Разделив объем указанной части слоя на объем одной ячейки, найдем число ячеек, заключенных в указанном объеме, а тем самым и искомое число стоячих волн:
где 
- объем куба. Чтобы найти число стоячих волн (типов колебаний) в объеме V и имеющих частоты в интервале от n до n + dn, нужно в эту формулу подставить значение k = 2 pn / v, где v – скорость распространения волн в среде. Тогда получим
(9.15)
Такой же результат получается и для объема произвольной формы.
Величину dZ (ν) можно рассматривать как число степеней свободы, характеризующее волновое поле в объеме V в интервале частот от n до n + dn.
Полученные результаты не зависят от физической природы стоячих волн и применимы как к упругим волнам в ограниченном объеме среды, так и к волнам другого типа, например, к тепловым волнам в твердых телах и электромагнитным волнам в замкнутой полости.
