I) Условие квазистационарности.
1) При изучении переменных полей и токов необходимо учитывать конечную скорость распространения электромагнитных волн в пространстве
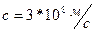- в вакууме
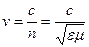- в среде
2) Порождённое магнитное поле, изменяющимся во времени электрическим полем. Явление э/м индукции.
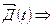
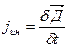
При малой частоте изменения переменного тока этими факторами можно пренебречь и считать, что электромагнитное поле распространяется мгновенно, токами смещения пренебречь и считать, что магнитное поле образуется только токами проводимости. Такие токи поля называются квазистационарными.
С физической точки зрения квазистационарным будет такой режим в цепи, при котором магнитное поле, создаваемое переменным током в любой момент времени практически такое же, как и у постоянного тока, т.е. так же распределено в пространстве и равно по величине во всех точках пространства, равноудалённых от данного проводника.
Электрическое поле зарядов в квазистационарной цепи совпадает со статическим полем распределённых зарядов в данный момент времени и в каждый момент оказывается неодинаковым на различных участках цепи, но если изменение тока происходят медленно, то мгновенные значения тока можно считать постоянными по цепи.
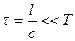(l – длина контура) – время распространения э/м возмущения
Для электрических цепей, имеющих размеры 10 метров, это условие хорошо выполняется, вплоть до частот в несколько мега герц.
(для синусоидального тока) 
II) Основные характеристики синусоидальных токов и напряжений.
Наиболее часто в науке и технике встречаются токи и напряжения, изменяющиеся по синусоидальному закону.
Мгновенные значения изменяются по закону
- амплитуды
Переменные синусоидальные токи характеризуются следующими параметрами:
Амплитуда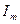 
- наибольшее положительное или отрицательное значение, которое принимает ток.
Период Т – наименьший интервал времени, по истечению которого мгновенные значения тока повторяются.
Частота f – число колебаний за единицу времени.
Фаза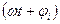 
- величина, определяющая мгновенное значение тока при заданной амплитуде в заданный момент времени.
Угловая частота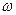 
- величина, показывающая число колебаний за 2 
секунд или величина, показывающая число радианов, на которое увеличивается фаза за одну секунду.
Для квазистационарных цепей справедливы законы Кирхгофа, Ома, сформулированные для цепей переменного тока, кроме мгновенных значений токов, напряжений и ЭДС.
§ 50 Колебательный контур.
Рассмотрим контур, состоящий из катушки индуктивности, сопротивления, конденсатора и источника ЭДС(L,R,C, 
).
По второму правилу Кирхгофа для мгновенных значений можно записать следующее
(
- мгновенное значение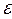 
)
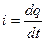
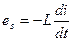
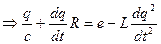после преобразования и сворачивания его в правую часть
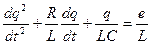- условие колебательного контура.
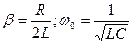- собственная частота колебания.
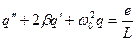
1) при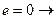 
в колебательном контуре свободные колебания
а) R=0 – незатухающие
б) R 
0 – затухающие
Свободные незатухающие колебания.
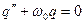- уравнение свободных незатухающих
колебаний.
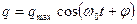- решение уравнений.
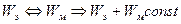
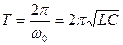
Свободные затухающие колебания.
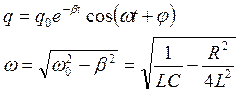
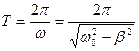
Характеристики затухающих колебаний.
1) коэффициент затухания, время релаксации
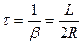
2) логарифмический декремент затухания - отношение двух амплитуд, взятых через период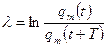 
Вынужденные колебания под действием синусоидального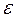 
.
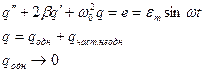
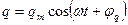
§ 51 Предоставление гармонической функции с помощью векторных диаграмм и комплексных чисел.
1) графическое представление гармонических функций (метод векторных диаграмм)
Сущность метода векторных диаграмм заключается в следующем: любую гармоническую изменяющуюся функцию можно представить в виде вращающегося веера с угловой скоростью 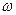(=угловой частоте изменения тока).
Модуль этого веера равен максимальному значению этой физической величины.
При рассмотрении электрической цепи синусоидального тока все напряжения и токи изменяются с одинаковой частотой и, потому их взаимное расположение на векторной диаграмме не будет изменяться со временем. Можно зафиксировать их взаимное расположение в некоторый момент (t=0). Дальнейший расчет и построение векторных диаграмм осуществляется по правилу Кирхгофа и законам Ома, записанных для цепей переменного тока, через амплитудные значения токов и направлений с учётом сдвига фаз.
Представление гармонических функций с помощью комплексных чисел.
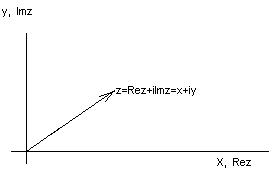
Возможность комплексного представления токов и напряжений (изменяющихся по синусоидальному закону) основана на формуле Эйлера.
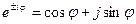
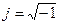
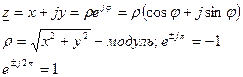
Дифференцирование и интегрирование комплексного числа по аргументу.
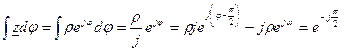
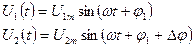
Рассмотрим представление токов и напряжений в комплексном виде
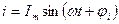. Такому току формально можно сопоставить комплексное число
Мнимая часть этого выражения определяет реальный ток
- комплексная амплитуда
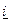- мгновенное значение комплексного тока
Аналогично можно написать и напряжение
