Закон эл/магнитной индукции. Правило Ленца.

I. ЭДС движущегося проводника

а) поступательно движущийся проводник

При движении проводника его свободные электроны под действием приводятся в движение относительно проводника — возникает ток – явление индукции в проводнике.

Дрейфовая скорость –

На каждый заряд . имеет две составляющие:

— ^ составляющая проводнику, которая проссумировавшись по всем носителям заряда на участке AC даст силу Ампера и при равном. движ. проводника она уравновешена внешней силой F.

— - составляющая направл. вдоль проводника – сторонняя сила, заставляющая заряды двигаться по проводнику, создающая индукционный ток.

Уравнение равномерного движения электрона

Þ пропорциональна скорости изменения магнитного потока.

б) Вращение проводника в магнитном поле (равномерно)

Аналогично поступ. движению возникает движение свободн. электр. Þ течет ток

Индуктивность.

Пусть в контуре по каким-либо причинам течет ток, магнитная индукция которого ~ току (сл-ие з-на Б-С-Л)

*

Индуктивность контура с током зависит от геометрических размеров и формы конура (от магнитных свойств среды, в которой находится контур)

Если вблизи контура с током находится диамагнетик или парамагнетик, то и зависит только от формы контура. Если ферромагнетик, то магн. поток через контур не пропорц. току. В этом случае также можно применить формулу

Пример:

Расчет индуктивности идеального соленоида

В некоторых случаях расчет индуктивности ведется по формуле

Она удобна, когда ток течет по тонким проводникам.

 

Закон эл/магнитной индукции. Правило Ленца.

Пусть произвольный контур с током находится во внешнем магнитном поле с индукцией . Из принципа суперпозиции и определения магнитного потока. Полный магнитный поток, пронизывающий контур, состоит из потока внешнего поля и потока собственного магнитного поля

При этом внешн. может изменяться со временем как из-за изменения внешнего поля во времени, так и из-за движения или отдельных его частей. Собственный магнитный поток может тоже меняться со временем (из-за изменения тока) и в результате изменения индуктивности контура (в результате деформации).

Опытным путем в 1831 г. Фарадей установил закон эл/магн. индукции: независимо от причин, вызывающих изменение полн. магнитного потока, в контуре возникает эл/движ. сила, называемая ЭДС индукции

Направление нормали к контуру и полож. напр. обхода связаны правилом буравчика и определяют знак F и e. ЭДС инд. > 0 если направление ее действия совпадает с положительным направлением обхода контура и отрицательно в противоположном случае. Под направлением действия ЭДС на некотором участке понимается направление действия сторонних сил на этот участок, т.е. то направление через участки контура с ЭДС при мысленном замыкании этого участка резистором

Второе слагаемое называется ЭДС самоиндукции. Оно появляется благодаря изменению во времени .

При решении задач можно пренебрегать индуктивностью контура () когда контур состоит из одного витка или рамки с малым количеством витков. Одним из критериев для оценки роли индуктивности служит сравнение и .

правило Ленца устанавливает знак (1883 г. – Ленц).

 

Природа эл/магнитной индукции.

$ 2 причины вызывающие возникновение :

- действие магнитной составляющей силы Лоренца на движущиеся заряды в движущихся проводниках. В этом случае F_л – сторонняя сила. Направление действия ЭДС инд. в движущемся проводнике совпадает с возможным направлением движения в нем положительных зарядов F_л.

рис:

- Вторая причина: возникновение вихревого поля в неподвижном контуре. Сторонние силы этого вихревого поля вызывают появление

В общем случае, когда контур движется и изменяется во времени магн. поля

В некоторых частных случаях формула является менее общей, чем .

Примеры:

§ 40 Явление самоиндукции.

Изменение собственного магнитного потока может происходить:

- За счет изменения тока I (t)

- За счет изменения индукции контура L (t)

Явление самоиндукции проявляется в контурах индукции при замыкании и размыкании индукции на внешний источник:

а) замыкании индуктивности на внешний источник

При резком размыкании контура с индуктивностью, e_S на короткое время может превысить рабочий e, что приводит к пробою изоляции индуктивности.

Явление индукции проявляется при возникновении в толще проводников при изменении тока через эти проводники вихревых токов.

Вихревые токи или токи Фуко в большинстве случаев являются вредными, т.к. в проводниках выделяется джоулево тепло и затраты мощности возрастают. Поэтому сердцев. трансф., якори генераторов набираются из отдельных пластин, стержней для того, чтобы изолировать их друг от друга.

Вихревые токи используются в индукционных печах, в которых за счет изменения магнитного поля в объеме расплавленного металла возбуждаются вихревые токи, вызывающие плавление этого металла.

 

Взаимная индукция.

 

На примере 2-х контуров

Ф₂₁ = L₂₁ ×I₁

Ф₁₂ = L₁₂ ×I₂

Ф₂₁ – магнитный поток, пронизывающий второй контур

L₂₁ – коэффициент вз. индукции

По теореме взаимной индукции L₂₁ = L₁₂ в случае, когда нет ферромагнетиков.

Когда ток в 1-м контуре изменяется, ~ нему изменяется магнитный поток Ф₁₂, создавая во 2-м контуре e взаимную индукцию.

Для нахождения взаимной индуктивн. контуров необходимо пропустить ток через какой-то контур, найти магнитный поток Ф₂₁, пронизывающий контур 2.

Дано:

N₁, N₂

l, S

а) m = const нет ферром.

б) m (I) – есть ферром.

 

а)

Явление взаимной индукции применяется в трансформаторах.

- коэффициент трансф.

Если пренебречь потерями на рассеяние магн. поля, токи Фуко, выделяющие тепло, то Ф пронизыв. вторичную оболочку будет таким же как и Ф, пронизывающий первичную оболочку.

 

§41. Магнитное поле в веществе.

Магнитное поле в веществе создается токами, текущими по проводникам (токи проводимости I), и движением заряженных частиц (ядер и электронов) внутри самих атомов и молекул (токи намагничивания ).

Согласно теории Бора электроны вращаются вокруг ядер по замкнутым траекториям (орбитам) и совершают вращение вокруг собственных осей, с которым связано количество движения (силы электрона).

Орбитальные и силовые движения элементарных частиц аналогичны круговым токам, они возбуждают магнитные поля. Магнетизм вещества обусловлен следующими причинами:

1. Орбитальным движением электрона вокруг атомных ядер

спиновый магнитный момент

3. Собственным вращением или спином. ядер. Однако спиновые моменты ядер в 1000 раз меньше магнитных спиновых моментов электронов и поэтому ими пренебрегают.

- сумма всех магнитных моментов электронов входящих в молекулу (атомы).

Атомы вещества, совершая беспорядочное тепловое движение, в отсутствии внешнего магнитного поля ориентированы хаотически. Возбуждаемые ими магнитные поля компенсируют друг друга. При вкл. внешнего магн. поля атомы ориентируются в сторону магн. поля, создаваемое собств. магн. полем , которое вместе с внешн. магн. полем образует результир. магн. поле . Вещество намагничивается. Тела, способные намагничиваться, называются магнетиками. Большинство веществ намагничиваются, но слабо. Сильными магнитными свойствами обладают ферромагниты (Fe, Ni, кобальт и некоторые сплавы).

Орбитальные и спиновые вращения электронов в отношении возбуждаемого поля эквивалентны некоторым токам, циркулирующим в атомах – молекулярные токи. Для вычисления B молекулярные токи усредняют по объему пространства, считая, что они распредел. непрерывно с плотностью - токи намагничивания. Обычные токи, текущие по проводам и связанные с упорядоченным движением заряж. частиц (электронов и ионов) называются токами проводимости.

Магнитное поле в веществе создается токами проводимости J и токами намагничив. J ’ и, если известно распределение плотностей тока (J(r),J’(r)), то можно вычислить по формулам для вакуума (Закон-Био-Савара-Лапласа, терема о циркуляции вектора магн. индукции), забыв о наличии вещества.

а) Теорема Гаусса для в веществе

 

б) Теорема о циркуляции

диф. форма

 

§ 42. Вектор намагниченности. Теорема о циркуляции магн. Поля в веществе.

I. Вектор намагнич.

Степень намагничивания магнет. характеризуется магн. моментом единицы V, создаваемого магнитными токами – вектор намагниченности.

Если обозначить < > - средний магнитный момент одной молекулы, а n – концентрация молекул, то

Рассмотрим одн. цилиндр. магнетик, (J = const). Молекулярные токи в этом магнетике текут согласованно и создаваемые ими магнитные поля усиливают друг друга.

Молекулярные токи в местах соприкосновения текут в противоположных направлениях и компенсируют друг друга.

Не скомпенсированные молекулярные токи, выходящие на боковую поверхность цилиндра образуют поверхностный ток намагничивания I’, создающий магн. поле как и все молекулярные токи вместе взятые. Магнитный момент тока I’ можно определить следующим образом:

i’ - поверхностный ток намагничивания

Замечание 1:

Если однородно намагничен косой цилиндр, то

Замечание 2:

Если магнит намагничен неоднородно, то цилиндр нужно выбрать бесконечно малым, так как в неоднородном магнетике наряду c i’ будут иметься объемные токи намагнич.

II. Вывод теоремы о циркуляции магнитного поля в веществе.

Возьмем произвольный замкнутый контур L, натянем на него поверхность S.

Одни молекулярные токи пересекают S дважды: раз в “+”, раз в “-“ направлении. Они не вносят вклад в ток намагничивания I’ через поверхность S. Другие молекулярные токи обвиваются вокруг L и пересекают поверхность S один раз. Они создают ток намагничивания i’. Выразим i’ через , окружив L бесконечно узкой трубкой, по поверхности которой будет течь ток намагничивания i’.

- теорема о циркуляции вектора намагничивания

Дифференциальная формула

Запишем теорему о циркуляции вектора магнитной индукции

Введем - вектор напряженности магнитного поля

- теорема о циркуляции

Т. циркуляция по замкнутому контору L равна алгебраической сумме токов, охвачиваемых этим контуром.

Дифференц. форма

Замечание:

Вектор - вспомогательный вектор, не имеющий глубокого физического смысла, но позволяющий во многих случаях упрощать расчет магнитного поля в веществе, аналогичный .

III. Связь между и

Рассмотрим линейный магнетик, тогда пропорциональна напряженности магнитного поля

c - магнитная восприимчивость магнетика.

В зависимости от c_м магнетики подразделяются на:

парамагнетики (O₂, Fe, платина)

диамагнетики (N₂, H₂O, CO₂, Ag) - вещества, которые намагничиваются противоположно магн. полю.

$ ферромагнетики, у которых зависимость J от H имеет сложный, нелинейный характер и наблюдается гистерезис, т.е. J зависит от предыстории магнетика.

В общем случае связь между :

Для линейных функций: Þ

 

§ 43. Граничные условия для векторов магнитного поля.

 

а) Граничные условия для вектора .

Рассмотрим границу раздела 2-х сред с отношением магн. прониц. m₁ и m₂. На границе раздела возьмем элементарный цилиндр, основания которого параллельны границе раздела. По теореме Гаусса для

B_1n =B_2n

б) Граничные условия для вектора .

Пусть вдоль границы раздела 2-х сред с m₁ и m₂ течет поверхностный ток проводимости с линейной плотностью . Возьмем элементарный прямоугольный контур, охватывающий этот линейный ток.

H_1t×l =H_2t×l=i×l Þ H_1t =H_2t=I

т.е. тангенсальная составляющая терпит скачок при переходе границы 2-х магнетиков.

Преломление линий , на границе раздела магн. (в случае отсутствия токов проводимости на границе)

Вывод: Ввиду того, что нормальная составляющая вектора не терпит разрыва на границе раздела 2-х магнетиков, то количество линий магнитной индукции в 1-ой и 2-ой среде будет одинаковым.

Ввиду того, что нормальная составляющая вектора терпит разрыв, то граница раздела является источником для и количество линий будет различным в 1-ой и 2-ой среде.

 

§44. Энергия магнитного поля.

п.1. Собственная магнитная энергия тока.

Когда замкнута на 1 по 2-му правилу Кирхгофа:

Найдем элемент. работу за dt

В процессе установления тока (когда Ф ­, dФ > 0) работа, которую совершает источник складывается:

- из Джоулевой теплоты, выделяемой в цепи на сопротивление R

- дополнительной работы против e_Si и

Рассмотрим случай, когда ферромагн. отсутствует

Ф = LI dФ = d(LI) Þ

При замыкании ключа из 1 в 2 энергия магн. поля превращается во внутреннюю энергию, и поэтому эта энергия $, когда $ ток и запасается контуром с током.

п.2. Энергия магнитного поля.

Т.к. ток окружен магнитным полем, встает вопрос, где локализована собств. этого поля. Ответ на этот вопрос был дан опытным путем при исследовании переменных магнитных полей (эл/магн. волн).

Т.к. ЭМВ заключают в себе и переносят определенную энергию, то энергия сосредоточена в самом поле.

Рассмотрим идеальный соленоид.

- объемная плотность энергии магн. поля

(*)

Замечание: для ферромагнетиков

идет на создание магнитного поля и на приращение внутренней энергии среды (на нагревание).

Покажем, что в случае справедливости формулы (*), формула для энергии магн. поля имеет вид:

Возьмем прямоугольный контур с током.

Окружим элемент трубки dS, ось которой совпадает c

Энергия сосредоточена во всей трубке

 

Просуммируем все элем. энергии всех трубок. Получим полную энергию магнитного поля

Замечание:

Т.к. Þ

Þ - эта формула позволяет найти индуктивность энергетическим способом и в некоторых случаях позволяет проще найти L, чем из определения.

Ввиду того, что в некоторых случаях трудно вычислить магнитный поток, создаваемый контуром с током.

Рассмотрим пример:

Рассмотрим коаксиальный кабель и найдем индуктивность на единицу длины.

По теореме о циркуляции рассчитаем этого кабеля

1) r £ a

2) a £ r £ b

3) B = 0

а) r a

 

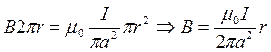
б)

 

в) r>b

 

 

При включении источников и в контурах возбуждается и в контурах возбуждается и при этом магнитный поток изменится

Дополнительная работа сторонних сил источника совершается против и образующихся при включении источников в первом и втором контуре.

- и эта дополнительная работа идёт на приращение энергии магнитного поля этих контуров

(*)

Энергия магнитного поля двух контуров с токами.

- собственная энергия тока

- собственная энергия тока

- энергия взаимодействия токов (**)

Получим формулу (*) непосредственно.

В некоторой точке пространства находится контур с током 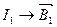, а контур с током .

аналогично.

Выводы:

1) из формул для собственной энергии магнитного поля видно, что собственные энергии магнитного поля величины строго положительны

2) энергии магнитного поля двух контуров с током не является величиной адиативной

3) взаимная энергия магнитного поля двух контуров с током может быть величиной как положительной, так и отрицательной

4) из формулы (**) можно получить ещё один метод расчета взаимной индуктивности без контуров ферромагнетиков