Множественная (многофакторная) регрессия. Оценка существенности связи

Множественная регрессия - регрессия между переменными у и x₁,x₂,…,x_m. Т. е. модель вида: у = f (x₁,x₂,…,x_m)+E

где у - зависимая переменная (результативный признак);

x₁,x₂,…,x_m- независимые, объясняющие переменные (признак-фактор); Е- возмущение, или стохастическая переменная, включающая влияние неучтенных факторов в модели.

Множественная регрессия применяется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах. Цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также их совокупное воздействие на моделируемый показатель.

Основные типы функций, используемые при количественной оценке связей: линейная функция: у = а₀ + a₁х₁ + а₂х₂,+... + a_mx_m. Параметры a_1, а_2, a_m, называются коэффициентами «чистой» регрессии и характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне; нелинейные функции: у=ах₁^b1 х₂^b2.... x_m^bm- - степенная функция; b₁, b₂..... b_m - коэффициенты эластичности; показывают, насколько % изменится в среднем результат при изменении соответствующего фактора на 1 % и при неизменности действия других факторов.

- гипербола;

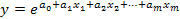- экспонента.

Отбор факторов при построении множественной регрессии. Включение в уравнение множественной регрессии того или иного набора факторов связано с представлением исследователя о природе взаимосвязи моделируемого показателя с другими эко­номическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.

2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией может привести к нежелательным последствиям - система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.

3. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

Методы построения уравнения множественной регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии к разным методам:

1) метод исключения (отсев факторов из полного его набора);

2) метод включения (дополнительное введение фактора);

3) шаговый регрессионный анализ (исключение ранее введенного фактора).

Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты.