Корреляционные параметрические методы - методы оценки тесноты свози, основанные на использовании, как правило, оценок нормального распределения, применяются в тех случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения.
Параметризация уравнения регрессии: установление формы зависимости; определение функции регрессии; оценка значений параметров выбранной формулы статистической связи Методы изучения связи - форму зависимости можно установить с помощью поля корреляции. Если исходные данные (значения переменных х и у) нанести на график в виде точек в прямоугольной системе координат, то получим поле корреляции При этом значения независимой переменной x (признак-фактор) откладываются по оси абсцисс, а значения результирующего фактора у откладываются по оси ординат. Если зависимость у от x функциональная, то все точки расположены на какой-то линии. При корреляционной связи вследствие влияния прочих факторов точки не лежат на одной линии.
Расчет показателей силы и тесноты связей Линейный коэффициент корреляции - количественная оценка и мера тесноты связи двух переменных. Коэффициент корреляции принимает значения в интервале от -1 до +1. Считают, что если этот коэффициент не больше 0,30, то связь слабая: от 0,3 до 0,7 - средняя; больше 0,7 - сильная, или тесная. Когда коэффициент равен 1, то связь функциональная, если он равен 0, то говорят об отсутствии линейной связи между признаками.
Коэффициент детерминации - квадрат линейного коэффициента корреляции, рассчитываемый для оценки качества подбора линейной функции.
Формула нелинейного коэффициента корреляции:
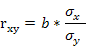
Корреляция для нелинейной регрессии Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно - индексом корреляции (R):
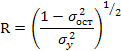
где 
- общая дисперсия результативного признака у,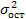 
- остаточная дисперсия, определяемая исходя из уравнения регрессии: ух = f (х). Корреляция для множественной регрессии. Значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата - коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или оценивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:
где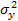 
- общая дисперсия результативного признака;
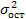- остаточная дисперсия для уравнения
у = f (x1,x2,…,xp)
