Для количественного описания взаимосвязей между экономическими переменными в статистике используют методы регрессии и корреляции.
Регрессия - величина, выражающая зависимость среднего значения случайной величины у от значений случайной величины х.
Уравнение регрессии выражает среднюю величину одного признака как функцию другого.
Функция регрессии - это модель вида у = л», где у - зависимая переменная (результативный признак); х - независимая, или объясняющая, переменная (признак-фактор).
Линия регрессии - график функции у = f (x).
2 типа взаимосвязей между х и у:
1) может быть неизвестно, какая из двух переменных является независимой, а какая - зависимой, переменные равноправны, это взаимосвязь корреляционного типа;
2) если х и у неравноправны и одна из них рассматривается как объясняющая (независимая) переменная, а другая - как зависимая, то это взаимосвязь регрессионного типа.
Виды регрессий:
1) гиперболическая - регрессия равносторонней гиперболы: у = а + b / х + Е;
2) линейная - регрессия, применяемая в статистике в виде четкой экономической интерпретации ее параметров: у = а+b*х+Е;
3) логарифмически линейная - регрессия вида: In у = In а + b * In x + In E
4) множественная - регрессия между переменными у и х1, х2... xm, т. е. модель вида: у = f(х1, х2... xm)+E, где у - зависимая переменная (результативный признак), х1, х2... xm- независимые, объясняющие переменные (признаки-факторы), Е- возмущение или стохастическая переменная, включающая влияние неучтенных факторов в модели;
5) нелинейная - регрессия, нелинейная относительно включенных в анализ объясняющих переменных, но линейная по оцениваемым параметрам; или регрессия, нелинейная по оцениваемым параметрам.
6) обратная - регрессия, приводимая к линейному виду, реализованная в стандартных пакетах прикладных программ вида: у = 1/a + b*х+Е;
7) парная - регрессия между двумя переменными у и x, т. е, модель вида: у = f (x) + Е, где у -зависимая переменная (результативный признак), x – независимая, объясняющая переменная (признак - фактор), Е - возмущение, или стохастическая переменная, включающая влияние неучтенных факторов в модели.
Корреляция - величина, отражающая наличие связи между явлениями, процессами и характеризующими их показателями.
Корреляционная зависимость - определение зависимости средней величины одного признака от изменения значения другого признака.
Коэффициент корреляции величин х и у (rxy) свидетельствует о наличии или отсутствии линейной связи между переменными:
где 
(-1; 1). Если: = -1, то наблюдается строгая отрицательная связь; = 1, то наблюдается строгая положительная связь; = 0, то линейная связь отсутствует.
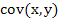- ковариация, т. е. среднее произведение отклонений признаков от их средних квадратических отклонений.
Коэффициент корреляции может служить мерой зависимости случайных величин.
Корреляция для нелинейной регрессии:
при R [0;1].
Чем ближе R к 1, тем теснее связь рассматриваемых признаков.
