Средние индексы.
Всякий агрегатный индекс может быть преобразован в средний арифметический из индивидуальных индексов. Для этого индексируемая величина отчётного периода, стоящая в числителе агрегатного индекса, заменяется произведением индивидуального индекса на индексируемую величину базисного периода.
Так, индивидуальный индекс цен равен  , откуда
, откуда  .
.
Следовательно, преобразование агрегатного индекса цен в средний арифметический имеет вид:
 =
=  =
= 
Аналогично индекс себестоимости равен  , откуда
, откуда  , следовательно,
, следовательно,  =
=  =
=  ,
,
Аналогично индекс физического объёма продукции (товарооборота) равен  , откуда
, откуда  , следовательно,
, следовательно,  =
=  =
= 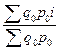
Расчеты недостающих индексов с помощью индексных систем.
Многие экономические индексы тесно связаны между собой и образуют индексные системы. Так, индекс цен связан с индексом физического объема товарооборота или физического объема продукции, образуя следующую индексную систему:
 или
или 
Произведение индекса цен на индекс физического объема товарооборота или продукции дает индекс физического объема товарооборота в фактических ценах, или индекс стоимости продукции.
Индекс себестоимости промышленной продукции связан с индексом физического объема продукции по себестоимости, образуя следующую индексную систему:
 или
или 
Произведение индекса себестоимости продукции на индекс физического объема дает индекс затрат в производстве.
Используя индексы системы, можно по двум известным индексам найти третий, неизвестный.
Изучение статистической связи.
Изучение взаимосвязей на рынке товаров и услуг — важнейшая функция работников коммерческих служб: менеджеров, коммерсантов, экономистов. Особую актуальность это приобретает в условиях развивающейся рыночной экономики. Изучение механизма рыночных связей, взаимодействия спроса и предложения, влияние объема и состава предложения товаров на объем и структуру товарооборота, формирование товарных запасов, издержек обращения, прибыли и других качественных показателей имеет первостепенное значение для прогнозирования конъюнктуры рынка, рациональной организации торговых процессов и решения многих вопросов успешного ведения бизнеса.
Статистика призвана изучать коммерческую деятельность с количественной стороны. Это осуществляется с помощью соответствующих приемов и методов статистики и математики.
Статистические показатели коммерческой деятельности могут состоять между собой в следующих основных видах связи: балансовой, компонентной, факторной и др.
Балансовая связь — характеризует зависимость между источниками формирования ресурсов (средств) и их использованием.

 — остаток товаров на начало отчетного периода;
— остаток товаров на начало отчетного периода;
 — поступление товаров за период;
— поступление товаров за период;
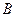 — выбытие товаров в изучаемом периоде;
— выбытие товаров в изучаемом периоде;
 — остаток товаров на конец отчетного периода.
— остаток товаров на конец отчетного периода.
Левая часть формулы характеризует предложение товаров
 , а правая часть — использование товарных ресурсов
, а правая часть — использование товарных ресурсов  .
.
Компонентные связи показателей коммерческой деятельности характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель, как множители:

В статистике коммерческой деятельности компонентные связи используются в индексном методе. Например, индекс товарооборота в фактических ценах  представляет произведение двух компонентов — индекса товарооборота в сопоставимых ценах
представляет произведение двух компонентов — индекса товарооборота в сопоставимых ценах  и индекса цен
и индекса цен  , т.е.
, т.е.
 .
.
Важное значение компонентной связи состоит в том, что она позволяет определять величину одного из неизвестных компонентов:
 или
или 
Факторные связи характеризуются тем, что они проявляются в согласованной вариации изучаемых показателей. При этом одни показатели выступают как факторные, а другие — как результативные.
Факторные связи могут рассматриваться как функциональные и корреляционные.
При функциональной связи изменение результативного признака  всецело зависит от изменения факторного признака
всецело зависит от изменения факторного признака  :
:

При корреляционной связи изменение результативного признака  не всецело зависит от факторного признака
не всецело зависит от факторного признака  , а лишь частично, так как возможно влияние прочих факторов
, а лишь частично, так как возможно влияние прочих факторов  :
:
 .
.
Примером корреляционной связи показателей коммерческой деятельности является зависимость сумм издержек обращения от объема товарооборота. В этой связи, помимо факторного признака — объема товарооборота  , на результативный признак (сумму издержек обращения
, на результативный признак (сумму издержек обращения  ) влияют и другие факторы, в том числе и не учтенные
) влияют и другие факторы, в том числе и не учтенные  . Поэтому корреляционные связи не являются полными (тесными) зависимостями.
. Поэтому корреляционные связи не являются полными (тесными) зависимостями.
Характерной особенностью корреляционных связей является то, что они проявляются не в единичных случаях, а в массе.
При статистическом изучении корреляционной связи показателей коммерческой деятельности перед статистикой ставятся следующие основные задачи:
1) проверка положений экономической теории о возможности связи между изучаемыми показателями и придание выявленной связи аналитической формы зависимости;
2) установление количественных оценок тесноты связи, характеризующих силу влияния факторных признаков на результативные.
Для того, чтобы установить, есть ли зависимость между величинами, используются многообразные статистические методы, позволяющие определить, во-первых — какие связи; во-вторых — тесноту связи (в одном случае она сильная, устойчивая, в другом — слабая); в-третьих — форму связи (т.е. формулу, связывающую величину  и
и  ).
).
В процессе изучения связи надо учитывать, что мы используем математический аппарат, но всегда надо иметь теоретические обоснования той связи, которую пытаются показать.
Переходим к методам изучения статистической связи.
Наиболее простой способ иллюстрации зависимости между двумя величинами — построение таблиц, показывающих, как при изменении одной величины меняется другая.
Пример.
| Производство молока в год. тыс. тонн. | Выработка продукции на 1 работающего, тыс. руб. |
| до 31 | 34,2 |
| 31 — 50 | 37,3 |
| 51 и выше | 42,7 |
Таблица показывает лишь согласованность в изменении двух величин, наличие связи. Но она не определяет ни тесноту связи, ни форму этой связи.
Для того, чтобы ответить на эти вопросы, необходимо использовать специальные статистические методы. Среди них есть очень простые и менее точные, более сложные и более точные. Но все они имеют один и тот же смысл.
Один из простых показателей тесноты корреляционной зависимости — показатель корреляции рангов. Разберем порядок вычисления этого показателя на примере.
Изучается товарооборот и суммы издержек обращения по ряду магазинов (в тыс. руб.).
Данные представлены таблицей 1.
| № магазина | Товарооборот | Издержки обращения |
Из таблицы видно, что с ростом товарооборота растут и издержки обращения. График еще раз это подтверждает.

Но в ряде случаев увеличение товарооборота ведет и к уменьшению издержек обращения, поскольку, помимо двух названных величин, в реальном процессе торговли участвуют и другие факторы, которые в рассмотрение не включены и носят случайный характер. Рассмотрим критерий тесноты связи, названный показателем корреляции рангов. От величин абсолютных перейдем к рангам по такому правилу: самое меньшее значение — ранг 1, затем 2 и т.д. Если встречаются одинаковые значения, то каждое из них заменяется средним. Итак:
| Товарооборот | Издержки |
| 7,5 | |
| 7,5 | |
Построим разности между рангами и возведем их в квадрат.
1. Если ранги совпадают, то ясно, что сумма их квадратов равна 0.


Связь полная, прямая.
2. Ранги образуют обратную последовательность
1 10
2 9 В этом случае 
3 8
.. Связь полная, обратная.
..
..
10 1
3. Среднее значение из двух крайних означает полное отсутствие связи:

4. Показатель корреляции рангов:
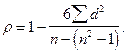
Показатель показывает, как отличается полученная при наблюдении сумма квадратов разностей между рангами от случая отсутствия связи.
Проанализируем показатель корреляции рангов.
1. Связь полная и прямая,  и
и 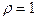
2. Связь полная и обратная, 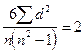 и
и 
3. Все остальные значения лежат между -1 и +1.
Построим показатель корреляции рангов для нашего примера:
| Товарооборот (ранг) | Издержки (ранг) | 
| 
|
| -3 | |||
| -2 | |||
| 7,5 | -0,5 | 0,25 | |
| 7,5 | 0,5 | 0,25 | |

|

Полученный показатель свидетельствует о достаточно тесной связи между товарооборотом и издержками.
Для определения тесноты корреляционной связи применяется коэффициент корреляции.
Коэффициент корреляции изменяется от -1 до +1 и показывает тесноту и направление корреляционной связи.
Если отклонения по  и по
и по  от среднего совпадают и по знаку, и по величине, то это полная прямая связь, то
от среднего совпадают и по знаку, и по величине, то это полная прямая связь, то  =+1.
=+1.
Если полная обратная связь, то  =-1.
=-1.
Если связь отсутствует, то  =0.
=0.
Наиболее удобной формулой для расчета коэффициента корреляции является:
 (1)
(1)
Коэффициент корреляции можно рассчитать и по другой формуле:
 (2), где
(2), где
 и
и 
Пример.
| Товаро- борот(х) | Издержки обращения (у) | 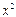
| 
| 
|

| 
| 
| 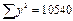
| 
|
Все необходимые данные для определения коэффициента корреляции есть в таблице, их лишь остается подставить в необходимую формулу.
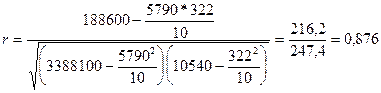
В ряде случаев возникает необходимость установления статистической связи между признаками, не имеющими количественного выражения.
Пример.
На предприятии работает группа станков. В силу организационно-технических причин, периодически возникают простои. Было проведено 133 наблюдения за работой станков на протяжении дня, при этом в 59 случаях были отмечены простои, соответственно в 74 случаях их не было. После рационализаторского предложения, направленного на уменьшение простоев, вновь было проведено наблюдение, но уже за 66 станками. При этом в 27 случаях были отмечены простои, в 39 — нет. В данном случае сопоставляются два признака, причем альтернативных.
1 признак — наличие или отсутствие рационального предложения;
2 признак — наличие или отсутствие простоев.
Ни тот, ни другой признак нельзя выразить числено. Поэтому введем следующие обозначения.
Первый признак (х): — наличие рационального предложения (1), отсутствие — (0).
Второй признак (у): — отсутствие простоев (1), наличие простоев (0).
Наши наблюдения представим таблицей:
 y
x y
x
|
Для центральной части таблицы введем специальные обозначения
| c | d |
| a | b |
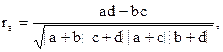 коэффициент корреляции (коэффициент ассоциации). Он так же меняется от -1 до +1 и для нашего примера равен:
коэффициент корреляции (коэффициент ассоциации). Он так же меняется от -1 до +1 и для нашего примера равен:

Очень маленький коэффициент. Показывает, что связь между рациональным предложением и уменьшением числа простоев очень мала. Конечно, простои уменьшились, но не на столько эффективно, как бы этого хотелось.
ВОПРОС 33
СТАТИСТИЧЕСКИЕ МЕТОДЫ
СТАТИСТИЧЕСКИЕ МЕТОДЫ — научные методы описания и изучения массовых явлений, допускающих количественное (численное) выражение. Слово “статистика” (от игал. stato — государство) имеет общий корень со словом “государство”. Первоначально оно относилось к науке управления и означало сбор данных о некоторых параметрах жизнедеятельности государства. Со временем статистика стала охватывать сбор, обработку и анализ данных о массовых явлениях вообще; ныне статистические методы охватывают со
бою практически все области знаний и жизнедеятельности общества.
Статистические методы включают в себя и экспериментальное, и теоретическое начала. Статистика исходит прежде всего из опыта; недаром ее зачастую определяют как науку об общих способах обработки результатов эксперимента. Обработка массовых опытных данных представляет самостоятельную задачу Иногда простая регистрация некоторых рядов наблюдений приводит к тому или иному значимому выводу. Так, если в некоторой стране из года в год растет объем валового внутреннего продукта, то это говорит об ее устойчивом развитии. Однако в большинстве случаев для обработки опытного статистическою материала используются математические модели исследуемого явления, основу которых составляют идеи и методы теории вероятностей.
Теория вероятностей есть наука о массовых случайных явлениях. Массовость означает, что исследуются огромные количества однородных явлений (объектов, процессов). Случайность же означает, что значение рассматриваемого параметра отдельного явления (объекта) в своей основе не зависит.и не определяется значениями этого параметра у других явлений, входящих в ту же совокупность. Основной характеристикой массового случайного явления является распределение вероятностей. Теорию вероятностей можно определить как науку о вероятностных распределениях — их свойствах, видах, законах взаимосвязей, распределении величин, характеризующих исследуемый объект, и законах изменения распределений во времени. Так, говорят о распределении молекул газа по скоростям, о распределениях доходов граждан в некотором обществе и т. д.
Эмпирически задаваемые распределения соотносятся с т. н. генеральной совокупностью, т. е. с наиболее полным теоретическим описанием распределений соответствующих массовых явлений. При этом во.многих случаях бывает нецелесообразно “перебирать” все элементы рассматриваемых совокупностей либо в силу чрезвычайно большого их числа, либо в силу того, что при наличии некоторого числа “перебранных” элементов учет новых не внесет существенных изменений в общие результаты. Для этих случаев разработан специальный выборочный метод исследования общих свойств статистических систем на основе изучения лишь части соответствующих элементов, взятых на выборку. Так, при оценке политических симпатий граждан некоторого региона или страны перед предстоящими выборами невозможно проводить сплошной опрос граждан. В этих случаях и прибегают к выборочному методу Чтобы выборочное распределение достаточно надежно характеризовало исследуемую систему, оно должно удовлетворять специальным условиям репрезентативности. Репрезентативность требует случайного выбора элементов и учета макроструктуры всего массового явления.
Распределения представляют наиболее общую характеристику массовых случайных явлений. Задание исходного распределения нередко предполагает построение математической модели соответствующих областей действительности. Построение и анализ таких моделей и составляет основную направленность статистических методов. Построенная математическая модель, в свою очередь, указывает, какие переменные следует измерять и какие из них имеют основное значение. Но главное в построении математической модели состоит в объяснении исследуемых явлений и процессов. Если модель достаточно полна, то она описывает зависимости между основными параметрами этих явлений.
Статистические методы в естествознании породили многие научные теории, привели к разработке важнейших фундаментальных направлений исследования — классической статистической физики, генетики, квантовой теории, теории цепных химических реакций и др. Следует, однако, отметить, что во многих случаях исходные вероятностные распределения задаются не путем непосредственной обработки массового материала. Вероятностная гипотеза чаще всего вводится гипотетически, косвенно, на основе теоретических предпосылок. Так, в учение о газах предположение о существовании вероятностных распределений было введено как гипотеза, на основе допущений о “молекулярном беспорядке”. Возможность подобного задания вероятностных распределений и проверки их справедливости обусловлена характером и природой самих распределений,
математическое выражение которых обладает самостоятельными характеристиками, достаточно независимыми от конкретных значений элементов.
Особые сложности возникают при применении статистических методов в изучении социальных явлений. Анализ общих направлений социальных процессов и внутренних механизмов, вызывающих конкретные статистические результаты, необычайно трудоемок. Так, благосостояние людей характеризуется весьма многими параметрами и соответствующими распределениями — уровнем доходов, участием в общественно-полезном труде, уровнем образования и здравоохранения и др. показателями жизнедеятельности человека. Выявление взаимосвязи этих распределений и тенденций их изменения требует решения многих сложных задач. Состояние общества можно определить через такие параметры, как внутренний валовый продукт, потребление энергии на душу населения, расслоение общества по доходам и т. п. Вместе с тем общество представляет собой необычайно сложную систему, а познание сложных систем основывается на разработке многих моделей, выражающих различные аспекты их структуры и функционирования. Соответственно, для более полной характеристики состояния общества требуется оперировать весьма многими параметрами и их распределениями. Так, говорят об экономической, производственной, сельскохозяйственной, социальной и многих других статистиках. Для объединения данных этих статистик в единую целостную картину необходимо выявление субординации, иерархии параметров, характеризующих состояние общества.
ВОПРОС 35






