Цели и задачи блока:
- отработка умений и навыков решения различных видов систем неравенств;
- коррекция умений, полученных на занятиях;
- развитие самостоятельности, умений самоконтроля.
Упражнения по совершенствованию и закреплению знаний и умений.
Решить системы неравенств:
1) 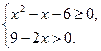 Решение:
Решение: 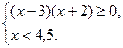

Ответ: (-∞; -2] U [3; 4,5).
2) 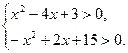 Решение:
Решение: 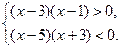

Ответ: (-3; 1) U (3;5).
3) 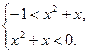 Решение:
Решение: 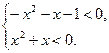
Рассмотрев первое неравенство, получим: D=-3<0, значит квадратный трехчлен при х є R имеет постоянно отрицательный знак, поэтому решением первого неравенства системы являются х 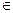 (-∞; +∞).
(-∞; +∞).
Второе неравенство системы x(x+1)<0 выполняется при x 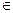 (-1; 0).
(-1; 0).
Ответ: (-1; 0).
4) 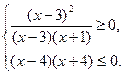 Для решения воспользуемся методом интервалов.
Для решения воспользуемся методом интервалов.
Решение первого неравенства: Решение второго неравенства:


Пересечение этих решений: 
Ответ: [-4; -1) U (3; 4].
Для развития самостоятельности, рефлексивных умений, проведения самоконтроля, учащимся может быть предложены задания для самостоятельного решения.
№ 1. Решить системы неравенств:
1) а)  Ответ: [6; +∞) б)
Ответ: [6; +∞) б) 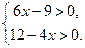 Ответ: (1,5;3).
Ответ: (1,5;3).
2)  Ответ: (-8; 7]. 3)
Ответ: (-8; 7]. 3) 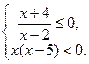 Ответ: (0;2].
Ответ: (0;2].
4) 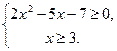 Ответ:
Ответ:  . 5)
. 5)  Ответ: (-4;0).
Ответ: (-4;0).
6) 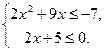
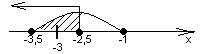 Ответ: -3.
Ответ: -3.
7) 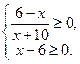
 Ответ: 6.
Ответ: 6.
8) 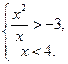
 Ответ: -2.
Ответ: -2.
9) Решите систему неравенств:
а). 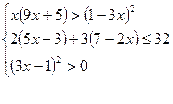 ; б).
; б). 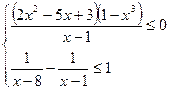 .
.
Ключевым элементом содержания в этих заданиях являются методы решения систем неравенств.
Вспомогательный элемент: числовые промежутки.
Итоговый тест по теме «Решение систем неравенств»
1. Множество решений какой системы неравенств указано на рисунке:
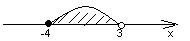
1) 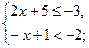 2)
2)  3)
3) 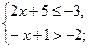 4)
4) 
К Ф О У
2. Множество решений какой системы неравенств указано на рисунке:
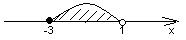
1)  2)
2) 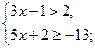 3)
3)  4)
4) 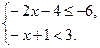
И Т О С
3. На каком из рисунков изображено множество решений системы неравенств
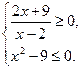
1)  2)
2) 
Н Д
3)  4)
4) 
П Н
4. Укажите множество решений системы неравенств
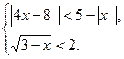
1) [1; 2,6], 2) решений нет, 3) (1; 2,6), 4) (0,6; 2,6).
Е Ы И Е
5. Какое из следующих чисел не содержится во множестве решений системы неравенств 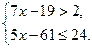 1) 3 2) 17 3)
1) 3 2) 17 3)  4) 5
4) 5
Ш Ц Х У
Итоговый контроль по теме «Решение неравенств и систем неравенств»
Контрольная работа.
В-1
1. Решите неравенства:
а) x+9>8-4x,
b) 3(y+4) ≥ 4 - (1-3y),
c) (x-3)(2x-3)+6x2≤2(2x-3)2
2. Решите систему неравенств:
а) 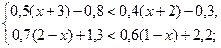
b) 
3.Решите неравенства методом интервалов:
а) 4x2 +3x -1 <0;
b) 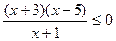 ;
;
с) 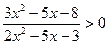 .
.
В-2
1. Решите неравенства:
a) 3x-7≤ 4x+8,
b) 3(y-2) + y < 4y+1,
c) (5-6x)(1+3x)+(1+3x)2 ≤ (1+3x)(1-3x).
2. Решите систему неравенств:
a) 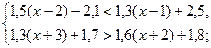
b) 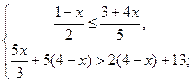
3.Решите неравенства методом интервалов:
а) 6x2+x-1>0;
b)  ;
;
с) 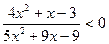 .
.
Заключение.
Так как материал подобран в соответствии с федеральным компонентом государственного стандарта общего образования с учетом требований кодификатора элементов содержания, то разработанная система задач дает хороший результат при осуществлении обобщающего повторения и подготовки к экзамену в 9 классе.
Список используемой литературы
1. Брагин В.Г., Грабовский А.И. Все предметы школьной программы в схемах и таблицах. Алгебра. – М.: Олимп, 1998.
2. Евдокимова Н.Н. Алгебра и начала анализа в таблицах и схемах. - Санкт-Петербург: Литера, 2005.
3. Алгебра 9 класс. Предпрофильная подготовка, итоговая аттестация-2009г. Под редакцией Ф.Ф.Лысенко.- Ростов-на-Дону: Легион, 2009.
4. Алгебра: учебники для 8, 9 классов общеобразовательных учреждений / Мордкович А.Г. и др.- М.: Мнемозина, 2005.
5. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. 9 класс/ Кузнецова Л.В., Бунимович Е.А., Пигарев Б.П., Суворова С.Б. – М.: Дрофа, 2010 г.
6. Студенецкая В.Н., Сагателова Л.С.. Сборник элективных курсов. Математика 8 – 9. – Волгоград: Учитель, 2006.
7. Тематические тесты «Алгебра 8», «Алгебра 9».- М.: Центр тестирования РФ.
8. С.А.Шестаков Сборник задач для подготовки и проведения письменного экзамена по алгебре за курс основной школы. Москва. Астрель. 2008 г.
Стартовая диагностика по теме «Неравенства и их решение».
1. Известно, что m<n. Какое из следующих неравенств неверно:
1) 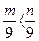 ; 2) 9m < 9n; 3) -9m < -9n; 4) m+9 < n+9.
; 2) 9m < 9n; 3) -9m < -9n; 4) m+9 < n+9.
2. Решите неравенство x2 ≥ 0,04.
1) x ≤ -0,2; 2) x ≥ 0,2; 3) x ≤ -0,2; x ≥ 0,2; 4) -0,2 ≤ x ≤ 0,2.
3. Решите неравенство 3х – 11 < 7x+9.
1) x < 5; 2) x < 2; 3) x < -5; 4) x > -5.
4. Решите неравенство 4x2 + 4x + 1 ≤ 0.
1) 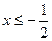 ; 2)
; 2) 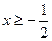 ; 3)
; 3)  ; 4) решений нет.
; 4) решений нет.
5. Сравните числа a и 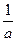 , если 0<a<1.
, если 0<a<1.
1) 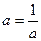 ; 2)
; 2)  ; 3)
; 3) 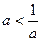 ; 4) нельзя сравнить.
; 4) нельзя сравнить.
6. Сравните числа х и  , если х > 1.
, если х > 1.
1) х = 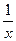 ; 2) х>
; 2) х> 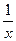 ; 3) х<
; 3) х< 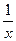 ; 4) нельзя сравнить.
; 4) нельзя сравнить.
7. Известно, что 0<a<с, с<b. Какое из следующих неравенств неверно:
1) b-a>0; 2) 
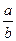 >1; 3) -3a>-3b; 4) b+c>a+c.
>1; 3) -3a>-3b; 4) b+c>a+c.
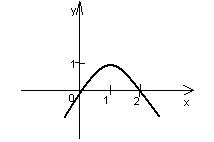 8. На рисунке изображен график функции y=2x-x2. Используя график,
8. На рисунке изображен график функции y=2x-x2. Используя график,
решите неравенство 2х-х2≤0.
 1)х=0; 2)х=2; 3) 0 ≤ x ≤ 2; 4) x ≤ 0; x ≥ 2.
1)х=0; 2)х=2; 3) 0 ≤ x ≤ 2; 4) x ≤ 0; x ≥ 2.
9. Используя графики функций y=x2-4 и y=4-x2, решите систему
неравенств 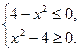
1) x ≤ -2; 2) x ≥ 2; 3) -2 ≤ x ≤ 2; 4) х=-2; х=2.
Ключ ответов к стартовой диагностики по теме «Неравенства и их решение».
Ключ ответов к тест по теме «Линейные неравенства»
Ключ к тесту (часть А). Ключ к тесту (часть С).
| В-1 | а | в | г | в | б |
| В-2 | б | а | а | г | а |
| В-1 | г | в |
| В-2 | в | в |
Ключ к тесту «Квадратные неравенства»:
| В-1 | в | г | б | б |
| В-2 | г | в | б | г |
Ключ ответов к тесту «Решение рациональных и дробно-рациональных неравенств методом интервалов.»:
| В-1 | а | в | г | в | б |
| В-2 | в | б | в | в | в |
Ключ к тесту «Решение неравенств»:
| В-1 | в | б | в | в | а | б | в | б | в |
| В-2 | в | в | б | б | б | г | а | б | в |
Ключ ответов к тесту по теме «Решение систем неравенств»:
2; 1; 4; 3; 1 (ФИНИШ).






