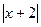1. Решить неравенство  2-м способом:
2-м способом:
(x+4)2≥1 <=> x2+8x+16≥1 <=>x2+8x+15≥0 <=>(x+3)(x+5)≥01 <=>x≤-5; x≥-3.
Ответ: (-∞;-5) U (-3; +∞).
2. Решить неравенство  1-м способом:
1-м способом:

3. Решить неравенство 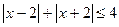 и указать наименьшие целые положительные решения:
и указать наименьшие целые положительные решения:
1. найти критические точки;
2. нанести найденные точки на ось;
3. расставить знаки для каждого модуля на получившихся промежутках, при переходе через критическую точку модуля знак меняется;
 4. решить неравенство на каждом промежутке, раскрывая модули согласно знакам;
4. решить неравенство на каждом промежутке, раскрывая модули согласно знакам;
x=-2 и x=2 точки, обращающие один из модулей в ноль (критические точки)


 | |||||||
| |||||||
| |||||||
|
|
|
|


|
|
|
|
|

|
1) при х<-2
|
-2x≤4,
 x≥-2.
x≥-2.
Неравенство на этом промежутке не имеет решения.
2) при -2≤x<2


|
 -x+2+x+2≤4.
-x+2+x+2≤4.
|
|


 0∙x≤0,
0∙x≤0,
хєR.
Решением неравенства является промежуток -2≤х<2.
3) 
 при х≥2
при х≥2
 х-2+х+2≤4,
х-2+х+2≤4,

|
х≤2.
Решением неравенства является х=2.
Ответ: [-2;2];
Задания для самостоятельного решения.
1.  . Ответ: нет решений.
. Ответ: нет решений.
2.  . Ответ: нет решений.
. Ответ: нет решений.
3.  . Ответ: -8<x<2.
. Ответ: -8<x<2.
4.  . Ответ: x<-2, x>0.
. Ответ: x<-2, x>0.
5.  . Ответ: (-∞;-5) U (3;+∞).
. Ответ: (-∞;-5) U (3;+∞).
Ключевым элементом содержания в этих заданиях является определение модуля и его свойства.
Упражнения по закреплению знаний и умений.
Цели и задачи блока:
- отработка умений и навыков решения различных видов неравенств;
- коррекция умений, полученных на занятиях;
- развитие самостоятельности, умений самоконтроля
Уровень А:
Решите неравенства:
1. 6-8x≥5x+19. Ответ: (-∞;-1].
2. 3x-11<7x+9. Ответ: (-5;+ ∞).
3. 7-2x<-23-5(x-3). Ответ: x<-5.
4. 8x+12>4-3(4-x). Ответ: x>-4.
5. 1-3x≤2x-9. Ответ: x≥2.
6. 7-5x≥-11-11x. Ответ: x≥-3.
7. (2-x)(x+3)≥0. Ответ: [-3;2].
8. (1-x)(x+4)>0. Ответ: (-4;1).
9. x2<0,81. Ответ: (-0,9; 0,9).
10. x2≥0,04. Ответ: (-∞;-0,2] U [0,2;+ ∞).
11. 4x2≤1. Ответ: -0,5≤x≤0,5.
12.  . Ответ: (-∞;-3] U [3;+ ∞).
. Ответ: (-∞;-3] U [3;+ ∞).
13. (x-2)2(x+1)>0. Ответ: (-1;2) U (2;+∞).
14. 9x2+6x+1>0. Ответ: (-∞;- 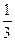 )U
)U  .
.
15. 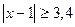 . Ответ: x≤-2,4; x≥4,4.
. Ответ: x≤-2,4; x≥4,4.
16.  . Ответ:
. Ответ: 
 .
.
17.  . Ответ: x>2,5.
. Ответ: x>2,5.
18.  . Ответ: y>-4.
. Ответ: y>-4.
19. 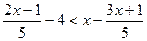 . Ответ: x – любое.
. Ответ: x – любое.
20.  . Ответ: x – любое.
. Ответ: x – любое.
21.  . Ответ: нет решений.
. Ответ: нет решений.
22. 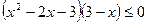 ;
;
23. 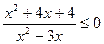 ;
;
24.  ;
;
25.  ;
;
26. 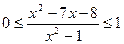
27. 
28.  ;
;
29.  ;
;
30.  ;
;
31.  ;
;
32.  ;
;
Уровень С:
Решить неравенства:
33. x4-4x3+4x2-1≤0. Ответ: [1-  ; 1+
; 1+  ].
].
34. x4-6x3+9x2-4≥0. Ответ: (-∞;  ] U [1; 2] U [
] U [1; 2] U [ 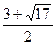 ; +∞).
; +∞).
35. |х2-5х|≥6. Ответ: (-∞; -1] U [2; 3] U [6; +∞).
36. Найти сумму целых решений неравенства  лежащих на
лежащих на
промежутке [-8; 8]. Ответ: 5+6+8=19.
37. 
Итоговой тест по теме «Решение неравенств».
Вариант I Вариант II
Часть 1.
№ 1. Найдите наибольшее целое решение неравенства:
4(х – 7) – 2(х + 3) ≤ -10. (х – 1) + 7(х + 2) < 27.
а) 7, в) 12, а) 2, в)1,
б) 0, г) 5. б) 0, г) 3.
№2. Найдите наименьшее целое решение неравенства:


а) 1, в) 2, а) 0, в) 2,
б) 0, г) 3. б) 1, г) 4.
№ 3. Решите неравенство:
-2х2 + 3х + 2 ≥ 0. -6х2 – х + 1 > 0.
а) свой ответ, а) свой ответ,
б) (-∞; -½) U (2; +∞), б) (-½; ⅓),
в) [-½; 2], в) (-∞; -½) U (⅓; +∞),
г) (-∞; -½] U [2; +∞). г) (-∞; -½] U [⅓; +∞).
№ 4. Решить неравенство:


а) [-3; 2], в) (-3; 2), а) (-∞; 1,5), в) (-∞; 1,5] U [8; +∞),
б) [-3; 2), г) (-3; 2]. б) (1,5; 8), г) (-∞; 1,5) U (8; +∞).
№ 5. Решите неравенство.
׀ х - 1׀ ≤ 2. ׀х - 4׀ ≥ 5.
а) -1 ≤ х ≤ 3, в) х < -1, а) х > 1, в) х ≥ -1,
б) х ≤ -1, г) х ≤ 3. б) х ≥ 9, х ≤ -1, г) х > 9.
№ 6. Сколько целочисленных решений имеет неравенство:
х2 + 7х ≤ 30. 3х – х2 > -40.
а) 12, в) 13, а) 8, в) 10,
б) 14, г) 0. б) 9, г) 12.
№ 7. Решить двойное неравенство:
-3  -1. -3
-1. -3 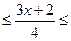 -1.
-1.
а)  < х ≤-3, в)
< х ≤-3, в)  ≤ х ≤-3, а)
≤ х ≤-3, а) 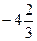 ≤ х ≤-2, в) х < -2,
≤ х ≤-2, в) х < -2,
б) х ≤  , г) х ≥ -3. б)
, г) х ≥ -3. б) 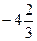 < х <-2, г) х >
< х <-2, г) х > 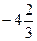 .
.
№ 8. При каких значениях х имеет смысл выражение:


а) (-∞; 2), в) (2; 3], а) (-∞; -2,5] U [8; +∞), в) (-∞; 2,5),
б) (2; 3), г) (2, 3]. б) (-∞; -2,5)U (8; +∞), г) (8; +∞).
Часть 2.
№ 9. При каких значениях параметра р квадратное уравнение имеет
действительные корни:
рх2 – 12рх – 3 = 0 (р + 2)х2 + 2рх + 1 = 0
№ 10. Решить неравенство: