неравенств» при подготовке к ОГЭ.
Симанькова Марина Львовна,
учитель математики ГБОУ средняя школа № 143
Введение.
Основной государственный экзамен выпускников 9 классов, является средством получения независимой оценки знаний учащихся и может считаться элементом общероссийской системы оценки качества образования.
Экзаменационная работа состоит из двух частей. Первая часть направлена на проверку усвоения учащимися основных алгоритмов и правил, понимание смысла важнейших понятий и их свойств, содержания применяемых приемов, а также умение применять знания в простейших практических ситуациях. Учащиеся должны продемонстрировать определенную систему знаний, умение пользоваться разными математическими языками, распознавать стандартные задачи в разнообразных формулировках.
Вторая часть направлена на проверку уверенного владения учащимися алгебраическим и геомнтрическим аппаратом, способностей к интеграции знаний из различных тем курса, владение широким набором приемов и способов рассуждения. Учащиеся должны продемонстрировать умение математически грамотно записать решение, приводя при этом необходимые пояснения.
Программа «Решение неравенств и систем неравенств» составлена для проведения занятий по обобщающему повторению в классах с различным уровнем усвоения учебного материала и различной мотивацией обучения в 9 классе.
Программа рассчитана на 17 часов и может являться программой элективного курса, или проводиться на дополнительных занятиях при оказании платных образовательных услуг.
Тематическое планирование занятий.
| № п/п | Изучаемая тема | Кол.часов |
| 1. | Решение линейных неравенств. | |
| 2. | Решение квадратных неравенств | |
| 3. | Решение рациональных и дробно-рациональных неравенств методом интервалов | |
| 4. | Решение неравенств, содержащих модуль | |
| 5. | Упражнения по закреплению знаний и умений. | |
| 6. | Решение систем неравенств | |
| Всего |
Цель занятий:
- развитие математических способностей; логического мышления, умения
анализировать, обобщать, делать выводы через усвоение различных методов решения неравенств, систем неравенств;
- преодоление психологического барьера, связанного с новой формой проведения итоговой аттестации по математике, и обретение уверенности в своих силах.
Задачи занятий:
- обобщить понятия: «неравенство», «система неравенств»;
- систематизировать основные методы решения неравенств, систем неравенств;
- научиться применять основные методы решения неравенств и их систем в новых нестандартных ситуациях;
- приобрести навыки работы с тестами, совершенствовать навыки самостоятельной работы, работы в группах;
- совершенствовать навыки самоконтроля.
Форма проведения занятий: групповая, парная, индивидуальная. Данные занятия помогут учащимся подготовиться к итоговой аттестации и осознанно выбрать профиль обучения в старшей школе. Каждая тема завершается итоговым контролем в форме теста, весь курс повторения завершается итоговым контролем в форме контрольной работы. В данной программе представлен практический материал, предложенный достаточно широким набором заданий разной степени сложности, содержащих теоретические, практические и контрольно-измерительные материалы, а так же комплект опорных схем по изучаемым темам, который рекомендуется использовать учащимся в индивидуальной работе.
Понятие «неравенство» – одно из фундаментальных понятий школьного курса математики.
Умение решать неравенства различных видов позволяет обеспечить базовую подготовку школьника для успешной сдачи ГИА. Кроме того, это может помочь ученику оценить как свой потенциал с точки зрения перспективы дальнейшего образования, так и повысить уровень своей общей математической культуры.
Учащийся должен знать:
- понятия «неравенство», «система неравенств»,
- виды неравенств и систем неравенств,
- основные методы решения неравенств и их систем.
Учащийся должен уметь:
- различать виды неравенств,
- выбирать рациональный способ решения для предложенного вида неравенств;
- выбирать и верно записывать ответ.
Теоретический материал.
Решение:
значение переменной, обращающее неравенство в верное числовое неравенство.

| Решить:
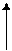 найти все решения или доказать, что их нет. найти все решения или доказать, что их нет.

| Равносильные: неравенства, имеющие одно и то же множество решений. |

|
  неравенство неравенство
| |
| можно переносить слагаемое из одной части в другую с противоположным знаком | можно умножать (делить) обе части на одно и то же положительное число | можно умножать (делить) обе части на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный. |
Название неравенства
Линейное неравенство с одной переменной
Квадратное неравенство с одной переменной
Общий вид
1) ax>b 3) ax<b
2) ax≥b 4) ax≤b
1) ax2 + bx + c>0 (а≠0)
2) ax2 + bx + c≥0 (а≠0)
3) ax2 + bx + c<0 (а≠0)
4)) ax2 + bx + c≤0 (а≠0)
Свойства числовых неравенств.
1. если a>b, то b<a;
2. если a>b, b>c, то a>c;
3. если a>b, с – любое число, то a+c>b+c;
4. если a>b, c>0, то ac>bc;
5. если a>b, c<0, то ac<bc;
6. если a>b, c>d, то a+c >b+d;
7. если a>0, b>0, c>0, d>0, a>b и c>d, то ac>bd;
8. если a>b>0, n – натуральное число, то an>bn;
9. если a>0, b>0, a>b, то  .
.
Решение линейных неравенств.
Цели и задачи блока:
- обобщить, систематизировать и несколько расширить знания учащихся о решении линейных неравенств;
- повторить виды числовых промежутков, их геометрическое изображение, обозначение и запись.
Числовые промежутки.
| вид промежутка | геометрическое изображение | обозначение | запись, с помощью неравенства |
| Интервал |

|

| a< x< b |
| Отрезок |

|

| a≤ x≤ b |
| Полуинтервал |
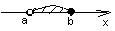
|

| a< x≤ b |
| Полуинтервал |
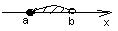
|

| а≤ x <b |
| Луч |

|

| x≥a |
| Луч |

|
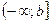
| x≤b |
| Открытый луч |

|
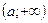
| x>a |
| Открытый луч |

|

| x<b |
Решение неравенств
ax>b
| a>0 | a<0 | a=0 | |
x> 
| x< 
| 0x>b | |
| b>0 | b<0 | b=0 0x>0 | |
| решений нет | 
| решений нет |
ax<b
| a>0 | a<0 | a=0 | |
x< 
| x> 
| 0x<b | |
| b>0 | b<0 | b=0 0x<0 | |

| решений нет | решений нет |
ax  b
b
| a>0 | a<0 | a=0 | |
x 
| x 
| 0x  b b
| |
| b>0 | b<0 | b=0
0x  0 0
| |
| решений нет | 
| 
|
ax 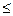 b
b
| a>0 | a<0 | a=0 | |
x 
| x 
| 0x 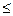 b b
| |
| b>0 | b<0 | b=0
0x 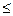 0 0
| |

| решений нет | 
|






