Цели и задачи блока:
- продолжить формирование умений решать квадратные неравенства;
- коррекция умений и навыков, полученных на уроках;
- развитие самостоятельности, умений самоконтроля.
Теоретический материал.
Квадратные неравенства – это неравенства вида ax2+bx+c>0, ax2+bx+c<0,
ax2+bx+c≤0, ax2+bx+c≥0, где а 
0.
Если квадратное уравнение ax2+bx+c=0 имеет два различных корня, то решение соответствующих квадратных неравенств можно свести к решению системы неравенств первой степени, разложив левую часть квадратного неравенства на множители по формуле ax2+bx+c =a(x-x 
)(x-x 
), используя свойства неравенств вида:
ab>0 
ab<0 
Например:
-2х2-5х+3>0,
2х2+5х-3<0,
2х2+5х-3=0,
x1,2 = 
x1=  , x2= -3;
2х2+5х-3=2(x- )(x+3);
Ответ: (-3; )
| 2(x- )(x+3)<0,
 или 
 
нет решения  .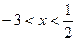
|
Решить квадратное неравенство можно графически. Квадратичная функция задается формулой у=ax2+bx+c, где a 0. Поэтому решение квадратного неравенства сводится к отысканию нулей квадратичной функции и промежутков, на которых квадратичная функция принимает положительные или отрицательные значения.
Графическое изображение.
| D | a>0 | a<0 |
| D<0 | 
| 
|
| D=0 |
 х1,2= 
|
 х1,2=
|
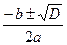
| D>0 |  х1,2= 
|  х1,2=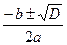
|
Решить квадратное неравенство можно методом интервалов:
-2х2-5х+3>0,
1. найти корни
2. нанести найденные корни на числовую ось, учитывая строгое или нестрогое неравенство, четность нечетность количества корней
3. поставить знак, справа от большего корня по старшему коэффициенту,
4. расставить остальные знаки при переходе через корень знак неравенства меняется, если корень встречается четное число раз, то при переходе через него знак сохраняется
5. выбрать нужный промежуток, в случае нестрого неравенства к решению неравенства добавить решение уравнения
2х2+5х-3=0
x1,2 =
x1= , x2= -3;
 | ||||||||||||||
| ||||||||||||||
 | ||||||||||||||
| ||||||||||||||
|
| |||||||||||||
 | ||||||||||||||
 |
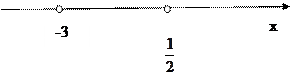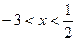
Ответ: (-3; )
Упражнения по закреплению знаний и умений.
№ 1. Решите квадратные неравенства тремя способами:
а) (х-2)(х+4)>0, в) x2-3x+2<0,
б) (x-3)(x+5)<0, г) x2-2x-3>0.
№ 2. Решите неравенства (любым способом):
а) х2 – 5х > 0, д) 4х ≤ -х2 е) х2+2х-15>0.
б) х2 > 25х, ж) 
1/3х2 > 1/9
в) х2 – 36 < 0, з) 
г) 3х2 + х + 2 > 0, и) 
№ 3. Найдите наименьшее целочисленное решение неравенства х2 + 7х ≤ 30.
№ 4. Найдите наибольшее целочисленное решение неравенства 3х – х2 > -40.
№ 5. Установите, при каких значениях х имеют смысл выражения:
а) 
в) 
б) 
г) 
№ 6. Сколько целочисленных решений имеют неравенства:
а) 15 – х2 + 10х ≥ 0, б) х2 + 5х – 8 < 0.
№ 7. При каких значениях параметра р квадратное уравнение 3х2 – 2рх – р + 6 = 0
а) имеет 2 различных корня; б) имеет 1 корень; в) не имеет корней.
Ключевым элементом содержания в этих заданиях является решение квадратных неравенств.
Вспомогательный элемент: решение квадратных уравнений, построение графика квадратной функции.
Перед проведением итогового теста можно предложить учащимся домашнее задание:
(2 – х)(х + 3) ≥ 0, (1 – х) (х + 4) > 0,
4х2 + 4х + 1 ≤ 0, 9х2 + 6х + 1 > 0,
х – х2 – 1 ≥ 0, 3х -х2 – 1 ≥ 0,
