


 .
.
Пример.
Дано: СП  , такой что
, такой что  ,
, 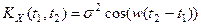 .
.
Найти: характеристики СП  .
.
Решение.



СП  называется интегрируемым потраекторно, если почти каждая его траектория – интегрируемая по Риману на
называется интегрируемым потраекторно, если почти каждая его траектория – интегрируемая по Риману на  функция, т.е.
функция, т.е.
 .
.
Тогда  является СВ. Если же СП
является СВ. Если же СП  является с.к.-интегрируем, то потраекторный и с.к.-интеграл совпадают с вероятностью 1.
является с.к.-интегрируем, то потраекторный и с.к.-интеграл совпадают с вероятностью 1.
Исследование данных с помощью автокорреляционного анализа
Нормированная автокорреляционная функция
 ,
,
может использоваться для ответа на вопросы:
1) являются ли данные случайными;
2) имеют ли данные тренд;
3) имеют ли данные сезонные (периодические) колебания.
В качестве оценки нормированной автокорреляционной функции случайного процесса, представленного временным рядом  длины
длины  принимают
принимают
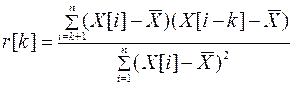 .
.
 – выборочный коэффициент автокорреляции для запаздывания на
– выборочный коэффициент автокорреляции для запаздывания на  периодов;
периодов;
 - выборочное среднее;
- выборочное среднее;
 – наблюдение в
– наблюдение в  -ый момент времени;
-ый момент времени;
 – число наблюдений.
– число наблюдений.
С ростом  точность оценки
точность оценки  заметно снижается На практике обычно максимальное значение
заметно снижается На практике обычно максимальное значение  .
.
Если последовательные значения временного ряда  не связаны друг с другом, то все коэффициенты
не связаны друг с другом, то все коэффициенты  . Если существует тренд, значения
. Если существует тренд, значения 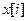 и
и  имеют сильную корреляцию, причем коэффициент автокорреляции существенно отличается от 0 для нескольких периодов запаздывания, а с увеличением задержки убывает до 0. Для сезонной компоненты значительный коэффициент корреляции
имеют сильную корреляцию, причем коэффициент автокорреляции существенно отличается от 0 для нескольких периодов запаздывания, а с увеличением задержки убывает до 0. Для сезонной компоненты значительный коэффициент корреляции  будет наблюдаться для значения
будет наблюдаться для значения  равному периоду и кратных ему значений.
равному периоду и кратных ему значений.
Как определить, что коэффициенты автокорреляции существенно отличаются от 0? Выдвигаем гипотезу  , что оцениваемый истинный коэффициент корреляции
, что оцениваемый истинный коэффициент корреляции  . Альтернативная гипотеза
. Альтернативная гипотеза  :
:  . Коэффициент
. Коэффициент  является оценкой параметра
является оценкой параметра  . Для проверки
. Для проверки  может быть использована статистика, имеющее распределение Стьюдента
может быть использована статистика, имеющее распределение Стьюдента  , где
, где 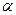 - уровень значимости,
- уровень значимости,  - число степеней свободы:
- число степеней свободы:
 ,
,
где  ,
,  ,
,  .
.
Таким образом, для каждого отдельного значения  мы можем вычислить требуемый доверительный интервал
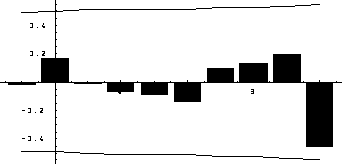
мы можем вычислить требуемый доверительный интервал  . Границы 95% доверительного интервала обычно наносятся на график корреляционной функции.
. Границы 95% доверительного интервала обычно наносятся на график корреляционной функции.
СПИСОК ЛИТЕРАТУРЫ к модулю 1
- Б.М.Миллер, А.Р.Панков. Случайные процессы в примерах и задачах.-М.: Изд-во МАИ,2001.
- А.Д.Вентцель. Курс теории случайных процессов. -М.: Наука,1975.
3. Е.С.Вентцель, Л.А.Овчаров. Теория случайных процессов и ее инженерные приложения. -М.: Наука,1991.
4. Л.В.Обухова, З.Я Молдовская, В.Ф.Князева. Теория вероятностей, математическая статистика и случайные процессы в примерах и задачах. -Киев: УМКВО,1991.
5. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. –М.: Мир, 1989.
6. Ханк Д. Бизнес-прогнозирование Изд. Дом «Вильямс», 2003
7. Дослідження ймовірнісних процесів з використанням пакетів прикладних програм: Навч. Посібнике. Ч. ІІ / Лісна Н.С., Шатовська Т.Б. Харків: ХТУРЕ, 1999.
8. Тюрин Ю.Н., Макаров А.А. Стохастический анализ данных на компьютере. М. Инфра, 1997






