Группы стрелочных переводов, уложенных на одном пути, образуют стрелочные улицы, которые различаются по конструкции: простейшие - под углом крестовины с расположением стрелочных переводов на боковом (рис.4.1 а) и основном (рис.4.2 б) путях; сокращенные, под углом наклона 
(рис.4.2), некратным и кратным марке крестовин стрелочных переводов; под двойным углом крестовины (рис.4.3); веерные неконцентрические (рис.4.4 а) и концентрические (рис.4.4 б); комбинированные (рис.4.5).
При расчете простейшей стрелочной улицы под углом крестовины определяются 
, координаты центров стрелочных переводов и вершины угла поворота кривой. Значения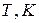 
и 
определяются из выражений (3.2) [лекция 3] и (3.3) [лекция 3]). Выражения для определения значений других величин приведены на рис.4.1.
При расчете сокращенной стрелочной улицы (рис. 4.2) определяется максимальное значение угла из зависимости: 
, где 
. Затем находится угол 
, значение тангенса 
для этого угла и значение тангенса Т для угла :
(4.1)
Необходимая расчетная ширина первого междупутья 
определяется как сумма проекций известных отрезков на вертикальную ось:
, (4.2)
где 
.
Приняв, что 
, рассчитываются координаты центров переводов и вершин углов поворота:
(4.3)
(4.4)
(4.5)
Координаты стрелочных переводов 3, 4 и вершин углов поворота на путях 3, 4 находятся добавлением к координатам центра перевода 2 проекций на оси 
и 
известных отрезков.
Затем проверяется величина вставки 
из выражения:
При расчете стрелочной улицы под двойным углом крестовины (рис 4.3) определяется расстояние между центрами переводов 1-2 и 2-3:
.
Далее определяется расчетная ширина первого междупутья и координаты центра перевода 2:
(4.6)
Расстояние 
между центрами переводов по улице, наклоненной под углом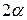 
, определяется из выражения:
. (4.7)
Для определения координат центров переводов и вершин углов поворота используются найденные координаты центра перевода 2, а также известные расстояния и 
. Координаты вершины угла поворота крайнего пути определяются по формуле:
. (4.8)
Проверка вставки осуществляется из выражения:
, (4.9)
где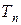 
- тангенс кривой на крайнем пути, = 
.
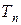Веерная стрелочная улица (рис. 4.4) имеет ось в виде ломаной линии. Угол направления ее меняется после примыкания каждого следующего пути.
При укладке неконцентрической улицы (рис. 4.4 а) с постоянным радиусом кривых междупутья в голове парка уширяются, вызывая увеличение объема земляных работ. Для устранения этого недостатка можно увеличивать радиусы кривых на каждом последующем пути.
В концентрических веерных стрелочных улицах (рис. 4.4 б) кривые участки концентричны и начинаются в одном створе. Недостатком веерной концентрической улицы является изменение вставки 
и, как следствие, появление рубок переменной длины при попутной укладке переводов.
Комбинированные стрелочные улицы (рис. 4.5) устраиваются при большом числе путей в парках. Они представляют собой различные комбинации простейших улиц с увеличением угла наклона к основному пути. Расчет координат центров переводов этих улиц осуществляется в порядке, который рассмотрен выше.
