Цель работы. Проверка надежности теста методом «тест-ретест» и методом расщепления «четное-нечетное», оценка плотности теста (консистенции).
Определение основных понятий. Надежность - характеристика теста, отражающая точность измерения и стабильность результатов. Количественно оценивается коэффициентом надежности
f =  = 1 -
= 1 -  ,
,
где S t - «истинная» дисперсия теста; S х - эмпирическая дисперсия теста; S е - дисперсия ошибки.
Прямая оценка коэффициента надежности невозможна (принципиально невозможно непосредственно определить S t и S е), поэтому применяют косвенные корреляционные методы, например метод «тест-ретест», метод расщепления.
Метод «тест-ретест» заключается в следующем: через некоторое время после первого проводится повторное тестирование с достаточным временным интервалом. Оценкой надежности служит коэффициент корреляции (Пирсона, ранговый или какой-либо иной, в зависимости от типа шкальных значений результатов тестирования).
Метод расщепления на части, в данной работе - на две части по принципу «четные-нечетные задания». В этом методе сопоставляются четные и нечетные номера заданий. Сила связи между этими двумя частями теста характеризует его надежность.
Возможно расщепление теста на любое количество частей. В предельном случае количество частей равно количеству заданий теста. Надежность в этом случае оценивается коэффициентом плотности (консистенции).
Математический аппарат
f =  ; (1)
; (1)
f = 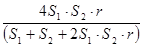 = d; (2)
= d; (2)
f = 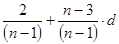 ; (3)
; (3)
f 1 = 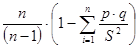 ; (4)
; (4)
где f - коэффициент надежности; r - коэффициент корреляции между двумя частями теста (Пирсона или ранговый); S 1, S 2 - среднеквадратичные отклонения 1-й и 2-й половин теста, соответственно; S 1 = 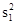 , S 2 =
, S 2 = 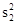 - дисперсии 1-й и 2-й половин теста, соответственно; п - количество заданий теста; d - символ для сокращения записи; f 1 - коэффициент консистенции; S - дисперсия всех задач теста; р - индекс трудности задачи в десятичной дроби (1/100); q = 1- р.
- дисперсии 1-й и 2-й половин теста, соответственно; п - количество заданий теста; d - символ для сокращения записи; f 1 - коэффициент консистенции; S - дисперсия всех задач теста; р - индекс трудности задачи в десятичной дроби (1/100); q = 1- р.
Значение коэффициента надежности теста редко превышает на практике 8.
Тест считается надежным при f > 6.
- Формула Спирмена-Брауна (1). Применяется, если дисперсии обеих частей теста равны. Это предположение проверяется с помощью критерия Фишера: F = S 1 /S 2 если эмпирическая статистика F превышает табличное значение F t,то гипотезу о равенстве дисперсий следует отклонить. В данном случае при 21 степени свободы, для уровня значимости 0,05 F t = 2,1.
- Формула Флангана (2). Применяется в случае неравенства дисперсий.
- Формула Кристофа (3). Применяется в случае малого количества заданий теста (п< 50).
- Формула Кьюдера - Ричардсона (4). Частный случай формулы Кронбаха для дихотомических интерпретаций ответов «правильно-неправильно».
Порядок работы. Студентам предлагается тест «Домино», с которым они работали на прошлом занятии.
Обработка данных
1.Составляется таблица (табл. 10.3.1), где Х 1 i - количество правильно решенных задач i -м испытуемым - показатель успешности работы i -го испытуемого в 1-м тестировании; Х 2 i -показатель успешности работы i -го испытуемого во 2-м; N - объем выборки испытуемых.
Таблица 10.3.1
Определение надежности методом «тест-ретест»
| i | X 1 | X 2 |
| … | ||
| N |
Вычисляется коэффициент корреляции r (Х 1, X 2).
2. Задания теста (после повторного тестирования) разбиваются на четные и нечетные. Составляется таблица (табл. 10.3.2), где У 1i, У 2i - количество испытуемых, правильно решивших соответствующую задачу; п - количество задач.
Таблица 10.3.2






