Функции нормального распределения
Функция НОРМРАСП
См. также НОРМОБР, НОРМСТРАСП, НОРМСТОБР, НОРМАЛИЗАЦИЯ.
Синтаксис:
НОРМРАСП (х; среднее; стандартное откл; интегральная)
Результат:
Рассчитывает нормальное распределение.
Аргументы:
х: значение, для которого вычисляется нормальное распределение;
среднее: средняя арифметическая распределения;
стандартное откл: стандартное отклонение распределения;
интегральная: логическое значение, определяющее форму функции. Если аргумент интегральная = 1, то функция НОРМРАСП рассчитывает интегральную функцию распределения; если аргумент интегральная = 0 - дифференциальную функцию распределения.
Математико-статистическая интерпретация;
Нормальный закон распределения (часто называемый законом Гaycca) имеет в статистике широкий круг приложений и занимает среди других законов распределения особое положение. Главная особенность, выделяющая нормальный закон среди других, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся условиях.
Доказано, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким-либо законам распределения, приближенно подчиняется нормальному закону; и это выполняется тем точнее, чем большее количество случайных величин суммируется. Основное ограничение, налагаемое на суммируемые величины, состоит в том, что они все должны играть в общей сумме относительно малую роль. Если ни одна из случайно действующих величин по своему действию не окажется преобладающей над другими, то закон распределения очень близко подходит к нормальному.
Такая закономерность проявляется во многих практических случаях. Например, еще Кетле (один из создателей научной статистики) обнаружил, что вариация в однородной группе характеризуется нормальной кривой. Если построить эмпирическую кривую распределения людей одной нации, пола и возраста по росту, весу, то она напоминает кривую Гаусса - Лапласа. Поэтому нормальное распределение часто применяется в тех случаях, когда истинный закон распределения известен, но вычисления по этому закону затруднительны, а аппроксимация его нормальным распределением допустима.
Примечание. Несмотря на широкое распространение, нормальное распределение не универсально. Если нет уверенности в его применимости, следует проверить возможность использования нормального распределения для описания случайной величины с помощью критериев согласия.
Уравнение для плотности нормального распределения имеет вид
f(x, 
,σ) = 
а уравнение нормальной функции распределения –
F(x, ,σ) = 
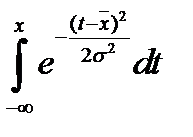= Ф 
Функция НОРМРАСП использует первое уравнение, если аргумент интегральная =0, и второе уравнение, если аргумент интегральная = 1. Так, формула =НОРМРАСП(42;40;1,5;0) рассчитает значение 0,109, а формула =НОРМРАСП(42;40;1,5;1) — значение 0,909.
Кривая плотности нормального распределения имеет симметричный холмообразный вид (см. рис. 6.2).
Максимальная ордината кривой соответствует точке х = = Мо = Ме. По мере удаления от этой точки плотность распределения падает, и при х 
± 
кривая асимптотически приближается к оси абсцисс. Изменение при постоянстве σ приводит к смещению кривой вдоль оси абсцисс, не меняя ее формы. С увеличением σ кривая становится более пологой, с уменьшением σ — более острой. Площадь, заключенная под кривой, асимптотически приближающейся к оси абсцисс, равна единице.
Для нормального распределения выполняются следующие равенства: μ1= μ3 = 0; μ2 = σ2; μ4 = 3σ4; А s = 0; Ek = 0.
Весьма важной практической задачей является определение вероятности того, что случайная величина попадет на заданный интервал вещественной оси (a, b). Для нормального распределения она определяется следующей формулой:
P(a<x<b) = Ф 
- Ф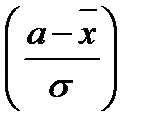 
Пример 6.1. Для закупки и последующей продажи мужских зимних курток фирмой было проведено выборочное обследование мужского населения города в возрасте от 18 до 65 лет в целях определения его среднего роста. В результате было установлено, что средний рост = 176 см, стандартное отклонение σ = 6 см. Необходимо определить, какой процент общего числа закупаемых курток должны составлять куртки 5-го роста (182—186 см). Предполагается, что рост мужского населения города распределен по нормальному закону.
Формула для решения задачи имеет следующий вид:
=НОРМРАСП(186;176;6;ИСТИНА) - НОРМРАСП(182;176;6;ИСТИНА) = 0,95221 -0,84134 = 0,11086= 11%.
Таким образом, куртки 5-го роста должны составлять приблизительно 11% общего числа закупаемых курток.
Функция НОРМОБР
См. также НОРМРАСП, НОРМСТРАСП, НОРМСТОБР, НОРМАЛИЗАЦИЯ, ДОВЕРИТ.
Синтаксис.
НОРМОБР (вероятность; среднее; стандартное откл)
Результат;
Рассчитывает обратное нормальное распределение.
Аргументы;
вероятность; вероятность, соответствующая нормальному распределению;
среднее: средняя арифметическая распределения;
стандартное откл: стандартное отклонение распределения.
Замечания;
Функция НОРМОБР использует для вычисления метод итераций и производит вычисления, пока не получит результат с точностью ±3 10-7. Если результат не сходится после 100 итераций, то функция помещает в ячейку значение ошибки #Н/Д.
Математико-статистическая интерпретация;
См. описание функции НОРМРАСП
Функция обратного нормального распределения используется в ситуациях, когда известна вероятность определенного значения случайной величины и необходимо рассчитать это значение.
Например, формула =НОРМОБР(0,90879;40;1,5) рассчитывает значение 42,00001 (сравните с формулой =НОРМРАСП(42;40;1,5;1), рассчитывающей значение 0,90879).
На практике часто встречается задача, обратная задаче вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно математического ожидания . Формула для вероятности попадания случайной величины на участок, симметричный относительно математического ожидания, имеет следующий вид:
P(
= 2Ф 
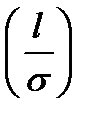- 1
где l — половина длины участка, симметричного относительно математического ожидания.
Пример 6.2. Для задачи, рассмотренной в примере 6.1, рассчитать границы интервала роста мужского населения города, вероятность попадания в который случайной величины роста составляет 0,95.
Для этого предварительно необходимо преобразовать аргументы НОРМОБР к стандартному виду, в результате чего имеем
l = НОРМОБР ((Р + 1)/2;0;σ).
После подстановки данных получим формулу = НОРМОБР ((0,95 + 1)/2;0;6), которая рассчитает значение 11,7598. Таким образом, границы искомого интервала составят 164,24 и 187,76 см.
В качестве границ интервалов часто берутся точки, отстоящие от математического ожидания на целое число стандартных отклонений (обычно σ, 2σ, 3σ). Приведем значения вероятности попадания нормально распределенной величины в интервалы с такими границами.
| Границы интервала | Вероятность |
| - σ, + σ
| 0,68269 |
| -2σ, + 2σ
| 0,95450 |
| - 3σ, + 3σ
| 0,99730 |
Функция НОРМСТРАСП
См. также НОРМРАСП, НОРМОБР, НОРМСТОБР, НОРМАЛИЗАЦИЯ.
Синтаксис
НОРМСТРАСП (z)
Результат;
Рассчитывает стандартное нормальное распределение.
Аргументы;
z: значение, для которого вычисляется стандартное нормальное распределение.
Математико-статистическая интерпретация;
См. описание функции НОРМРАСП.
Стандартное нормальное распределение представляет собой не что иное, как «обычное» нормальное распределение, у которого среднее равно нулю, а стандартное отклонение — единице.
Особое выделение функции стандартного нормального распределения связано с тем, что она используется при вычислении нормальных функций с другими значениями и σ (отличными от 0 и 1 соответственно). Практически во всех учебниках по теории вероятностей и теории статистики приведены таблицы для функции стандартного нормального распределения.
Например, формула =НОРМСТРАСП((42—40)/1,5) рассчитает значение 0,90879, такое же, как и формула =НОРМРАСП(42;40;1,5;1) (см. описание функции НОРМРАСП).
Функция НОРМСТОБР
См. также НОРМРАСП, НОРМОБР, НОРМСТРАСП, НОРМАЛИЗАЦИЯ.
Синтаксис;
НОРМСТОБР (вероятность)
Результат;
Рассчитывает обратное стандартное нормальное распределение.
Аргументы;
вероятность; вероятность, соответствующая нормальному распределению.
Математико-статистическая интерпретация;
См. описание функций НОРМСТРАСП, НОРМОБР
Функция обратного стандартного нормального распределения используется в ситуациях, когда известна вероятность определенного значения случайной величины и необходимо рассчитать это значение.
Например, формула =НОРМСТОБР(0,69146) вычисляет значение 0,5 (сравните с формулой =НОРМСТРАСП(0,5), рассчитывающей значение 0,69146). Кроме того, формула =НОРМСТОБР (0,69146) может быть заменена формулой =НОРМОБР(0,69146; 0;1), также рассчитывающей значение 0,5 (см. описание функции НОРМОБР).
Функция НОРМАЛИЗАЦИЯ
См. также НОРМРАСП, НОРМОБР, НОРМСТРАСП, НОРМСТОБР ДОВЕРИТ.
Синтаксис;
НОРМАЛИЗАЦИЯ (х; среднее; стандартное откл)
Результат;
Рассчитывает нормализованное значение для нормального распределения.
Аргументы;
х: нормализуемое значение;
среднее: средняя арифметическая распределения;
стандартное откл: стандартное отклонение распределения.
Математико-статистическая интерпретация;
Нормализация (нормирование) заключается в переходе от случайной величины х с математическим ожиданием и дисперсией σ2 к нормированной величине
t = 
получаемой в результате деления центрированной случайной величины х - на стандартное отклонение σ. Величину t называют нормированной или стандартизованной случайной величиной, которая самостоятельно не применяется, а входит составной частью в выражение интегральной функции нормального распределения (см. описание функции НОРМРАСП).
Функцию НОРМАЛИЗАЦИЯ удобно использовать в качестве аргумента функции НОРМСТРАСП.
Например, формула =НОРМСТРАСП(НОРМАЛИЗАЦИЯ (42;40;1,5)) рассчитывает значение 0,90879, такое же как и формулы =НОРМСТРАСП((42-40)/1,5) и =НОРМРАСП(42;40;1,5;1) (см. описание функций НОРМСТРАСП и НОРМРАСП).
Функция ДОВЕРИТ
См. также НОРМАЛИЗАЦИЯ, НОРМОБР НОРМРАСП, НОРМСТОБР, НОРМСТРАСП, ZTECT.
Синтаксис;
ДОВЕРИТ (альфа; станд откл; размер)
Результат;
Рассчитывает значение предельной ошибки выборки.
Аргументы;
альфа: уровень значимости, используемый для вычисления уровня надежности. Уровень надежности равняется 100 (1—альфа) % (например, альфа, равное 0,05, означает 95%-ный уровень надежности).
станд. откл: стандартное отклонение генеральной совокупности для интервала данных, предполагается известным;
размер: размер выборки.
Математико-статистическая интерпретация;
Одна из основных задач выборочного исследования состоит в том, чтобы на основе характеристик выборочной совокупности получить достоверные суждения об этих характеристиках в генеральной совокупности. Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются разностью между значением характеристики в генеральной совокупности и ее значением, вычисленным по результатам выборочного наблюдения. Для средней арифметической это расхождение определяется по формуле
Зная выборочную среднюю величину признака (
) и предельную ошибку выборки (
), можно определить границы, в которых заключена генеральная средняя :
- 
+
Интервал - ; + получил название доверительного интервала.
Вероятность того, что случайный интервал ( - ; + ) содержит в себе достоверную, но не известную наблюдателю характеристику , получила название доверительной вероятности γ. Иногда говорят, что вероятность γ характеризует надежность статистической оценки , и наряду с термином «доверительная вероятность применяют для γ термин «надежность».
Примечание. Необходимо отметить, что в качестве аргумента функции ДОВЕРИТ используется не доверительная вероятность γ, а уровень значимости α = 1 — γ, откуда γ =1-α.
Предельная ошибка выборки связана со средней ошибкой выборки 
следующим соотношением:
= t
где t — коэффициент доверия (определяется в зависимости от того, с какой доверительной вероятностью нужно гарантировать результаты выборочного обследования).
Известный русский математик А. М. Ляпунов дал выражение конкретных значений множителя t для различных значений доверительной вероятности γ в виде функции
Ф (t) = Р{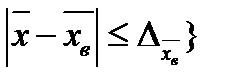 
= 
На практике пользуются готовыми таблицами этой функции, которые приведены практически в каждом учебнике по теории вероятностей или теории статистики.
В Microsoft Excel для нахождения значения доверительной вероятности γ (значения функции Ф (t)) можно использовать формулу =2НОРМСТРАСП(t)- 1, а для нахождения значения коэффициента доверия t — формулу =НОРМСТОБР((γ+1)/2) (см. описание функции НОРМАЛИЗАЦИЯ, НОРМРАСП, НОРМОБР, НОРМСТРАСП, НОРМСТОБР).
Применение функции ДОВЕРИТ для решения практических задач рассмотрим на следующем примере.
Пример 6.3. В результате выборочного обследования жилищных условий жителей города, осуществленного на основе собственно-случайной повторной выборки, получен следующий ряд распределения (табл. 6.3). Требуется с уровнем надежности 95% определить границы интервала, в который попадет средний размер общей площади.
Табл.6.3
| Общая площадь, приходящаяся на 1 чел., м2 | До 5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 | 30 и более |
| Число жителей |
Рассмотрим решение задачи в среде Microsoft Excel (табл. 6.4).
Табл. 6.4
В табл. 6.4 приведены два варианта решения задачи. Первый вариант основан на последовательном применении рассмотренных выше формул для нахождения предельной ошибки выборки . Во втором варианте (более быстром) используется функция ДОВЕРИТ.
Содержимое ячеек в табл. 6.4:
массивы В3:В9 и D3:D9 содержат исходные данные задачи;
массив С3:С9 содержит середины рассматриваемых интервалов;
ячейка D10 содержит формулу =СУММ(D3:D9) — рассчитывается размер выборочной совокупности n.
ячейка D11 содержит формулу =СУММПРОИЗВ(С3:С9;D3:D9)/D10 — определяется значение выборочной средней ;
ячейка D12 содержит формулу =(СУММПРОИЗВ(Е3:Е9;D3:D9)/D10))*D10/(D10-1) — вычисляется значение генеральной дисперсии σ 2ГЕН
ячейка D13 содержит формулу =KOPEHЬ(D12) — рассчитывается значение стандартного отклонения σ ГЕН для генеральной совокупности;
ячейка D14 содержит формулу =D13/KOPEHЬ(D10) — определяется значение средней ошибки выборки 
;
ячейка D15 содержит формулу =НОРМСТОБР((0,95+1)/2) — вычисляется значение коэффициента доверия t для уровня надежности 95 %;
ячейка D16 содержит формулу =D15*D14 — рассчитывается значение предельной ошибки выборки ;
ячейка D17 содержит формулу =D11-D16 — определяется нижняя граница генеральной средней - ;
ячейка D18 содержит формулу =D11+D16 — рассчитывается верхняя граница генеральной средней + ;
ячейка D19 содержит формулу =ДОВЕРИТ(0,05;D13; D10), демонстрирующую альтернативный вариант нахождения предельной ошибки выборки.
Таким образом, на основании проведенного выборочного обследования с уровнем надежности 95 % можно предположить, что средний размер обшей площади, приходящейся на 1 человека, в целом по городу лежит в пределах от 18,56 до 19,45 м.
Перечислим другие непрерывные распределения, реализованные в среде Microsoft Excel:
Функции гамма-распределения;
Функции бета-распределения
Функции логарифмического нормального распределения
Функции экспоненциального распределения
Функция распределения Вейбулла
Функции χ 2 – распределения (распределения Пирсона)
Функции F-распределения (Фишера)
