Краткая теория к лабораторной работе №6
ГЛАВА 6. Генерация случайных чисел
Краткие сведения из теории статистики
Одним из фундаментальных в статистическом анализе является понятие случайной величины. Случайной называется переменная величина, принимающая в зависимости от случая те или иные значения с определенными вероятностями.
В практических задачах обычно используются дискретные и непрерывные случайные величины.
Дискретной случайной величиной называется такая случайная величина, множество возможных значений которой либо конечно, либо бесконечно, но счетно.
Непрерывной случайной величиной называется такая случайная величина, которая может принять любое значение из некоторого конечного или бесконечного интервала.
Чтобы дать полное математическое описание случайной величины, нужно указать множество ее значений и соответствующее случайной величине распределение вероятностей на этом множестве.
Каждое отдельное значение непрерывной случайной величины обладает нулевой вероятностью. Однако, несмотря на данное обстоятельство, нахождение возможных значений случайной величины в различных интервалах обладает различными и отличными от нуля вероятностями. Таким образом, для непрерывной случайной величины, так же как и для дискретной, можно определить закон распределения, но несколько в ином виде, чем для дискретной. Для этого используют понятие функции распределения случайной величины.
Функцией распределения случайной величины X называется функция F(x), задающая вероятность того, что случайная величина X принимает значение, меньшее x, т.е.
F(х)=Р(X<х).
Иногда функцию F(x) называют интегральной функцией распределения.
Функция распределения вероятностей непрерывной случайной величины дает полную вероятностную характеристику ее поведения. Однако способ задания непрерывной случайной величины с помощью функции распределения не является единственным. Ее можно задать с помощью другой функции, которая называется дифференциальной функцией распределения или плотностью распределения. В некотором смысле эта функция более удобна, чем интегральная функция F(x), так как последняя не в полной мере дает представление о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси. Решить эту задачу позволяет дифференциальная функция распределения, которая является первой производной интегральной функции распределения:
f(x)=F'(х).
График дифференциальной функции распределения f(x) называется кривой распределения. Кривая распределения, выражающая общую закономерность данного типа распределения, называется теоретической кривой распределения.
В статистике широко используются различные виды теоретических распределений — нормальное распределение, биномиальное, распределение Пуассона и др. Каждое из теоретических распределений имеет специфику и свою область применения. Чаще всего в качестве теоретического распределения используется нормальное распределение, занимающее особое положение в статистических исследованиях.
Справочная информация по технологии работы
Режим работы «Генерация случайных чисел» служит для формирования массива случайных чисел, распределенных по одному из заданных теоретических распределений.
В зависимости от выбранного теоретического распределения (подрежима работы) меняются и параметры диалогового окна Генерация случайных чисел. Общими параметрами для всех подрежимов являются:
1. Число переменных — вводится число столбцов значений, которые необходимо разместить в выходном диапазоне. Если это число не введено, то все столбцы в выходном диапазоне будут заполнены.
2. Число случайных чисел - вводится число случайных значений, которое необходимо вывести в каждом столбце выходного диапазона. Каждое случайное значение будет помещено в строке выходного диапазона. Если число случайных чисел не будет введено, все строки выходного диапазона будут заполнены.
Примечание. Данное поле деактивировано при модельном распределении.
3. Распределение - в данном раскрывающемся списке выбирается тип распределения, которое необходимо использовать для генерации случайных чисел.
4. Случайное рассеивание - вводится «стартовое» число для генерации определенной последовательности случайных чисел. Впоследствии это число можно снова использовать для получения той же самой последовательности случайных чисел.
Примечание. Данное поле деактивировано при модельном распределении.
5. Выходной интервал/Новый рабочий лист/Новая рабочая книга.
Рис. 6.1
Технология работы во всех подрежимах режима работы «Генерация случайных чисел» является одинаковой, особенность заключается только в задании параметров, характерных для конкретных распределений (как правило, они задаются в области Параметры).
На рис. 6.1 изображено диалоговое окно подрежима работы, предназначенного для генерации случайных чисел, распределенных по нормальному закону. В этом окне в области Параметры задаются характеристики нормального закона распределения - математическое ожидание (поле Среднее) и стандартное отклонение (поле Стандартное отклонение).
Строить графики интегральных и дифференциальных функций распределения удобно с помощью мастера диаграмм Microsoft Excel. Для этого необходимо предварительно сформировать интегральные и дифференциальные массивы значений, для чего следует воспользоваться функцией НОРМРАСП (см. подразд. 6.3.1), используя в качестве ее аргументов сгенерированную последовательность случайных чисел.
Графики интегральной и дифференциальной функций нормального распределения при 
= 0 и σ2 = 1 показаны на рис. 6.2.
Рис. 6.2
Для генерации последовательности случайных чисел, распределенных по биномиальному закону в области Параметры задаются вероятность успеха при одном испытании (поле Значение р) и число испытаний (поле Число испытаний).
Графики биномиального распределения строятся на основе интегрального и дифференциального массивов значений, формируемых с помощью функции БИНОМРАСП (см. подразд. 6.4.1). Так как биномиальное распределение является дискретным, то точечные графики, построенные с помощью мастера диаграмм Microsoft Excel, необходимо дорабатывать вручную с использованием панели Рисование. На рис. 6.3 изображен график дифференциальной функции биномиального распределения при р = 0,75 и n = 10.
Рис. 6.3
Примечание. Подрежим работы «Распределение Бернулли» является частным случаем подрежима «Биномиальное распределение» при n = 1.
Для генерации последовательности случайных чисел, распределенных по равномерному (прямоугольному) закону, в области Параметры задаются нижняя и верхняя границы интервала, в котором будут заключены сгенерированные числа (поле Между...).
Понятие равномерного распределения на отрезке [а, в] соответствует представлению о выборе точки из этого отрезка «наудачу». Особое значение имеет равномерное распределение на отрезке [0; 1]. Оказывается, что для имитации на ЭВМ случайных явлений самой различной природы достаточно получить на ЭВМ последовательность значений случайной величины, равномерно распределенной на отрезке [0; 1].
Интегральная и дифференциальная функции случайной величины, равномерно распределенной на отрезке [0; 1], имеют следующий вид:
0 при х< 0;
F(x,a,b) = х при 0 ≤ х ≤ 1;
1 прих > 1;
f(x,a,b) = 1 при 0 ≤ х ≤ 1;
0 при х < 0 и х > 1.
Для генерации последовательности случайных чисел, распределенных по закону Пуассона, в области Параметры задается интенсивность появления событий (поле Лямбда).
Графики пуассоновского распределения строятся на основе интегрального и дифференциального массивов значений, формируемых с помощью функции ПУАССОН. На рис. 6.5 показан график дифференциальной функции распределения Пуассона при λ = 0,8.
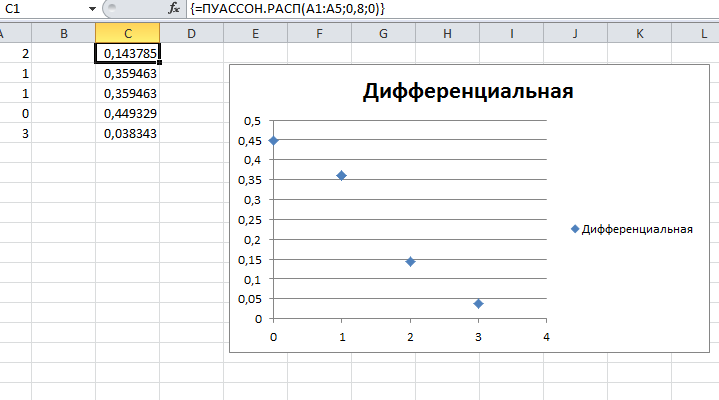Рис.6.5
Подрежим работы «Дискретное распределение» служит для генерации последовательности случайных чисел, распределенных по закону, задаваемому пользователем.
