РАЗДЕЛ 8. ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
· Описываются свойства собственных интегралов, зависящих от параметра
· Описываются свойства несобственных интегралов, зависящих от параметра
ДИФФЕРЕНЦИРОВАНИЕ ПОД ЗНАКОМ СОБСТВЕННОГО ИНТЕГРАЛА. ПРАВИЛО ЛЕЙБНИЦА. СЛУЧАЙ, КОГДА ПРЕДЕЛЫ ИНТЕГРИРОВАНИЯ ЗАВИСЯТ ОТ Y
Теорема1. (Правило Лейбница). Пусть 
непрерывны на 
. Тогда 
дифференцируема на 
, причём 
(В концах отрезка производные односторонние)
Пусть 
, 
, 
. Тогда
Подынтегральная функция непрерывна по 
, значит, интегрируема. По теореме Лагранжа получаем:
, 
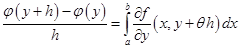По условию, 
и, значит, равномерно непрерывна на ; поэтому для любого 
существует 
такое, что из неравенств 
, 
следует, что
При 
, 
, 
получаем, что если 
, то для любого 
,
откуда
и 
Теорема 2. В условиях предыдущей теоремы пусть,, где, дифференцируемы на. Тогда
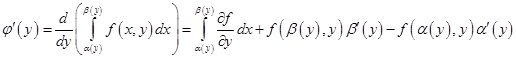
(обозначим 
, 
, 
)
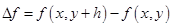Дословно повторяя рассуждения предыдущей теоремы, получим, что при 
Далее, по теореме о среднем, ввиду непрерывности 
(
)
При получаем
Пример 1.
ИНТЕГРИРОВАНИЕ ПОД ЗНАКОМ СОБСТВЕННОГО ИНТЕГРАЛА
Теорема 3. Пусть. Тогда существуют и равны интегралы
Обозначим первый из этих интегралов 
, второй - 
.
Положим 
, 
, .
Докажем, что эта функция непрерывна по совокупности переменных.
Оба слагаемых стремятся к 0(первое- ввиду непрерывности 
,второе – по теореме о среднем для определённого интеграла) при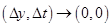 
. Кроме того,
по свойству интеграла с переменным верхним пределом, поэтому для
имеем, по правилу Лейбница,
(это обозначение).
Но для 
, по теореме Ньютона-Лейбница имеем:
где 
Итак, 
,
выполнено равенство
. При 
получаем теорему.
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА. РАВНОМЕРНАЯ СХОДИМОСТЬ
Пусть 
определена при 
и любом 
(
- множество значений параметра y) и пусть для любого сходится интеграл
(1)
Этот интеграл будем называть сходящимся несобственным интегралом, зависящим от параметра.
Понятие несобственного интеграла, зависящего от параметра, во многом схоже с понятием функционального ряда
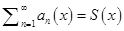(2)
Функция соответствует 
, переменой интегрирования в (1) соответствует индекс суммирования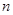 
в (2), параметру 
в (1) соответствует переменная в (2).
По определению несобственного интеграла
.
Рассмотрим интеграл
(3)
(интеграл (3) аналогичен частичной сумме ряда (2), 
)
Сходимость (поточечная) интеграла (1) в области означает, что для любого существует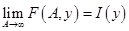 
, т.е.
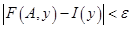(4)
Напомним, что аналогичное (4) условие поточечной сходимости ряда 
на множестве 
имело вид
(5)
сходный с определением поточечной сходимости интеграла (1) на множестве .
При рассмотрении теории рядов мы отмечали, что требование поточечной сходимости(5) ряда (2) не является достаточным для того, чтобы выполнялись равенства:
(6)
(7)
(8)
Аналогичная проблема возникает и для несобственного интеграла, зависящего от параметра. Например, если взять 
, 
, то полагая в нем 
, получаем, что 
, т.е. 
равен постоянной величине, от 
не зависящей и 
.
Однако если рассмотреть интеграл
, то легко показать, что он расходится. Действительно, при 
, поэтому при выполняется равенство 
, а эта последняя величина не имеет предела при 
.
Для того, чтобы обеспечить выполнение равенств (6)-(8), для рядов было введено понятие равномерной сходимости, определяемое условиями
(9)
Равномерность сходимости состоит в том, что число 
не зависит от 
.
Аналогично (9) определяем равномерную относительно сходимость интеграла на множестве параметров :
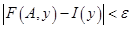(10)
Отметим, что отсутствие равномерной сходимости означает
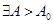
(11)
Пример. Интеграл
(12)
сходится при любом 
. Действительно, 
. Рассмотрим, при 
,величину 
,т.е.
(условие было использовано в предпоследнем равенстве (при замене переменной сохранился верхний предел интегрирования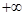 
)).
Эта величина меньше 
, т.е. 
, если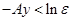 
, т.е. если 
, .
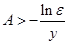Если область изменения параметров такова, что для всех выполняется неравенство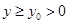 
, то сходимость интеграла (12) равномерная, т.к. тогда положим 
(здесь 
- фиксированная величина) и и имеют место неравенства 
т.е. 
. Таким образом, условие (10) выполняется.
Однако в области , когда значения параметра могут быть сколь угодно близкими к числу 0, сходимость интеграла (12) перестанет быть равномерной. Действительно, тогда существует , например можно взять любое число, удовлетворяющее неравенствам 
, и для любого 
существуют 
и , например, 
, с условием 
, или 
, такие что 
.
Значит, выполняется (11) и интеграл (12) не сходится равномерно в области .
