Рассмотрим уравнение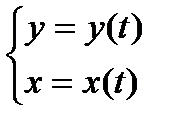 
где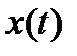 
, 
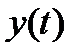− дважды дифференцируемые функции на некотором промежутке 
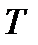; пусть, кроме того, функция 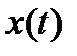строго возрастает (или убывает) на 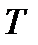и ни в одной точке этого промежутка 
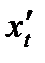не равна 0. В пункте 20.7 доказано, что в этом случае уравнения (2) задают функцию 
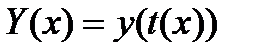, и производная этой функции равна
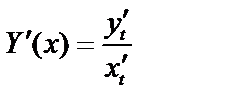
Бывает также, что производные по параметру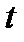 
обозначают так: 
, 
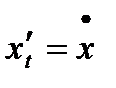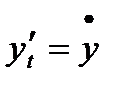. Тогда формула (3) принимает вид: 
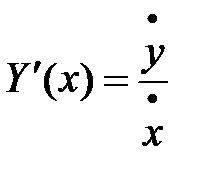. Найдём вторую производную функции 
:
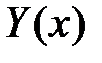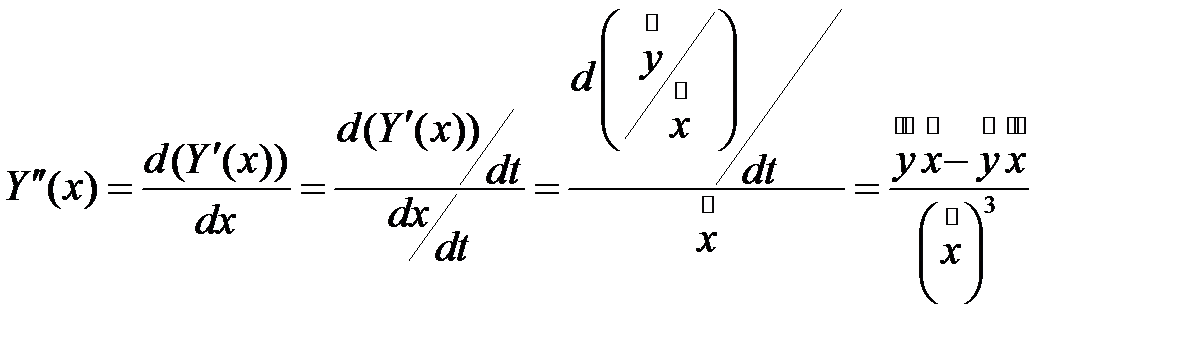
ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Однородную линейную функцию называют линейной формой.
Напомним, что если функция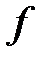 
дифференцируема в точке 
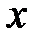, то
дифференциалом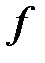 
в x называют линейную форму 
.
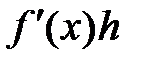Аналогично, если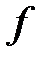 
дифференцируема дважды в точке 
,
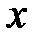то ее вторым дифференциалом называют квадратичную форму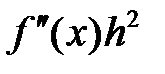 
.
Вообще, n-ым дифференциалом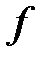 
в точке x будет n-ичная
форма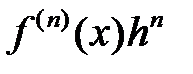 
(в предположении, что 
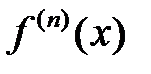существует).
Для n-го дифференциала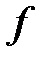 
в точке x используют обозначение 
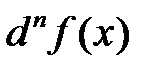или, более
строго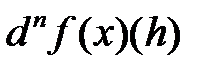 
.
Таким образом, по определению,
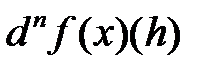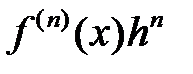= для всех 
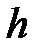Î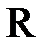 
.
Согласно этому определению,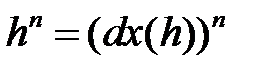 
есть n-я степень функци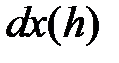и 
и
потому используют обозначение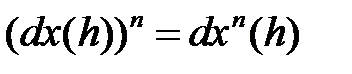 
. Тогда
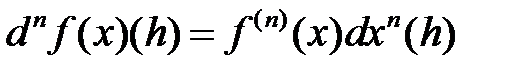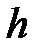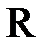для всех Î , или
.
Форма записи n-го дифференциала не инвариантна
уже при n=2. Действительно, подставляя вместо 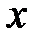дифференцируемую
функцию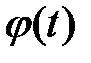 
в левую часть формулы (при n=2), получим
= 
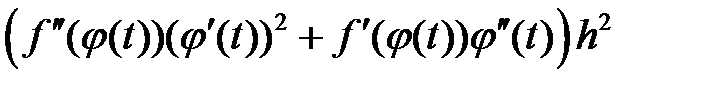
а в результате такой же подстановки в правую часть, имеем
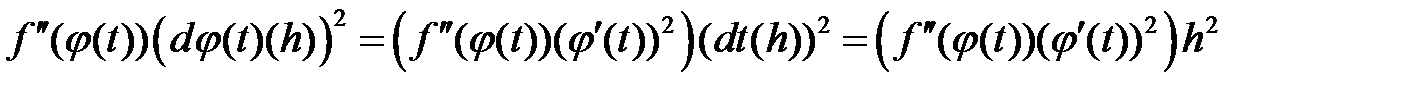.(5)
Правые части этих формул отличаются слагаемым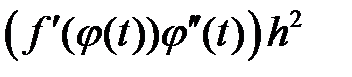 
.
Вообще говоря, это слагаемое не равно нулю. Однако если 
- линейная функция,
то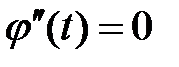 
и, вообще, для любого 
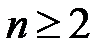имеет место равенство 
,
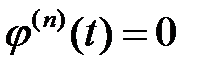откуда следует, что формула будет верна и для линейной функции .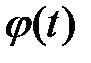
ЭЛАСТИЧНОСТЬ И ЕЁ СВОЙСТВА
Определение. Пусть функция y определена в некоторой окрестности точки x, дифференцируема в точке x и y(x) ≠ 0. Эластичностью функции y в точке x называется величина
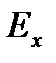(y) =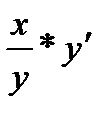 
Если предположить, что x 
, то можно рассматривать величину
,
которая характеризует величину относительного изменения y в результате соответствующего относительного изменения x; например, процентное изменение спроса на товар в результате однопроцентного изменения цены этого товара. Тогда следует, что
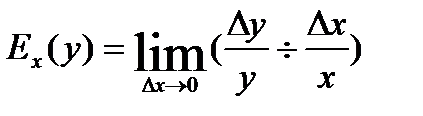
Если y>0, то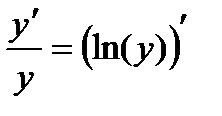 
по теореме о производной сложной функции.
Если y<0, то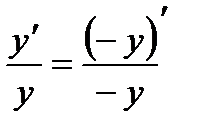 
,
поэтому при y<0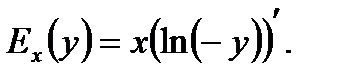 
Следовательно,
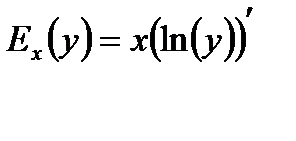при y>0
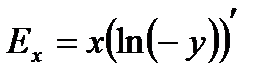при y<0
Обе эти формулы можно объединить в одну: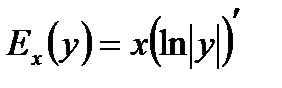 
Теорема. 1) Если u, v – функции, для которых определены эластичност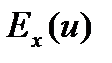и 
и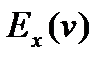 
,
То: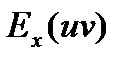 
= 
+ 
- .
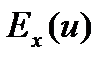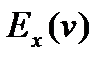
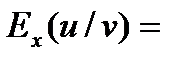
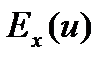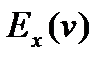2) Если для функции y = y(x), определённой на интервале 
, существует обратная функция x = x(y), причём y дифференцируема на этом интервале и ни в одной точке x интервала не выполняется равенство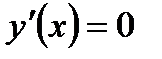 
, то для всех x 
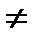0, y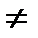 
0 определены величины 
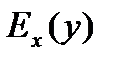и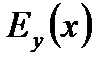 
,
причём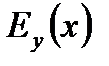 
= 
.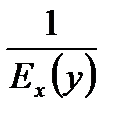