РАЗДЕЛ 3. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
· Излагаются основные свойства производных и дифференциалов функций
· Рассматриваются вопросы дифференцируемости функций одной и нескольких переменных
ПРОИЗВОДНАЯ, ЕЁ СМЫСЛ И ОСНОВНЫЕ СВОЙСТВА. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ
Пусть 
определена в окрестности 
точки 
.
Определение. Числовую функцию 
называют дифференцируемой в точке , если для всех 
имеет место равенство
,
где число 
не зависит от 
, а 
при 
и бесконечно малая функция 
непрерывна в точке 
, т.е. 
.
Числовую функцию называют дифференцируемой на множестве 
, если дифференцируема в каждой точке 
.
Теорема. Функция 
, дифференцируемая в точке 
, непрерывна в этой точке.
Пример функции 
(эта функция не дифференцируема в точке 
), показывает, что утверждение, обратное теореме, неверно.
Производная
Пусть определена в окрестности точки .
Поскольку на множестве 
определена функция 
и - предельная точка для , то можно ставить вопрос о существовании предела разностного отношения в точке .
Определение. Число 
(если оно существует) называют производной функции в точке и обозначают символом 
.
Итак,
,
при условии, что предел существует.
Для обозначения производной также используется символ 
.
Скорость прямолинейного движения есть производная перемещения как функции времени. Часто полезно, по аналогии с этим, трактовать и производную любой функции в точке как скорость изменения функции в этой точке.
Пример. Линейная функция 
имеет производную в каждой точке, и ее производная 
- постоянная. В частности, постоянная имеет всюду производную, равную нулю, а тождественная функция - производную, равную единице.
Пример. Квадратичная функция 
имеет производную в каждой точке, и ее производная равна 
.
Пример. Модуль не имеет производной в точке 0.
В этом примере мы встретились с ситуацией, когда существуют 
и 
. Эти величины называются, соответственно, правой и левой производной и обозначаются 
. Для существования производной необходимо и достаточно, чтобы существовали и были равны друг другу.
Теорема. Функция , дифференцируемая в точке 
, имеет в этой точке производную, и последняя равна коэффициенту 
.
Теорема показывает, что функция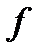 
, дифференцируемая в точке 
, представима в виде
,
где 
при 
.
Теорема. Функция 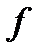, имеющая производную в точке , дифференцируема в этой точке.
Таким образом, сказать, что числовая функция дифференцируема в данной точке, или что она имеет в этой точке производную, одно и то же. Нахождение производной функции 
у функции 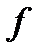называют дифференцированием этой функции.
КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ
Как и нахождение скорости неравномерного движения, нахождение касательной к кривой линии - одна из основных задач, решение которых привело к созданию дифференциального исчисления.
Рассмотрим частный случай задачи о касательной, когда линией служит график функции.
Определение. Пусть числовая функция 
определена на невырожденном промежутке 
и непрерывна в его точке 
(так что расстояние 
от соответствующей точки 
графика до его точки 
, 
, стремится к нулю при 
). Касательной к графику функции в точке 
называют такую прямую, проходящую через , что отношение расстояния 
от точки до этой прямой к расстоянию 
от до стремится к нулю при (т.е. что 
бесконечно мало по сравнению с 
при ).
Таким образом, кривая, обладающая в точке 
касательной, почти сливается с ней вблизи этой точки.
Теорема. Если функция , определенная на промежутке, дифференцируема в его точке , то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен 
.
Таким образом, нахождение углового коэффициента касательной (как и нахождение скорости) приводит к вычислению производной.Уравнение касательной имеет вид 
Замечание. Секущая 
имеет угловой коэффициент 
(см. рис. 15). Таким образом теорема показывает, что угловой коэффициент касательной в точке есть предел углового коэффициента секущей при .
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
