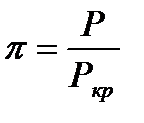В момент равновесия
dU = TdS - PdV
dH = TdS + VdP
dF = -SdT - PdV
dG = -SdT + VdP
Из сопоставления этих выражений видно, что здесь две пары переменных, а именно параметры характеризующие работу (P и V) и параметры характеризующие теплоту (T и S).
Частные производные этих функций являются основными параметрами состояния:
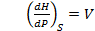

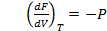

Отсюда вытекает важное свойство этих функций:
Через каждую из этих функций и ее производную можно выразить в явной форме любую термодинамическую величину (свойство) системы. Поэтому каждая из этих функций дает полную характеристику системы и следовательно эти функции называют характеристическими, а переменные естественными.
Графическая связь между характеристическими функциями:
| P | V | ||
| S | T | ||
| U | H | F | G |
Эта связь обратимая, т.е. характеристическими функциями могут быть не только термодинамические потенциалы, но и параметры: S, T, P, V, если их выразить как функцию других величин.
T = f(P, G); T = f(V, F); S = f(P, H); S = f(U, V)
Уравнение максимальной работы Гиббса-Гельмгольца
Рассмотрим систему, в которой протекает работа в условиях постоянства давления и температуры.

Заменим 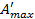 на разность значений изобарных потенциалов:
на разность значений изобарных потенциалов:
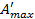 = Н1 – ТS1 – (Н2 – ТS2) = ΔH + TΔS = - QP + TΔS
= Н1 – ТS1 – (Н2 – ТS2) = ΔH + TΔS = - QP + TΔS
 , тогда
, тогда
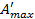 = - QP + TΔS = - QP + T
= - QP + TΔS = - QP + T 
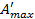 = - QP + T = - QP + T 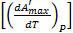
| - уравнение максимальной работы Гиббса-Гельмгольца в дифференциальной форме |
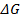 = =  + T + T 
|
Уравнение Гиббса-Гельмгольца связывает максимальную полезную работу химической реакции, протекающей идеально равновесно и тепловой эффект этой же реакции, но когда она протекает полностью неравновесно. Из этого уравнения можно рассчитать тепловой эффект реакции, если известна максимальная полезная работа и ее зависимость от температуры.
Для обратного расчета, т.е. расчета 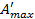 по известной величине QP, которую находят экспериментально, это уравнение необходимо проинтегрировать:
по известной величине QP, которую находят экспериментально, это уравнение необходимо проинтегрировать:
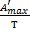 = =  + J + J
| - уравнение Гиббса-Гельмгольца в интегральной форме |
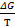 = =  + J + J
|
J – константа интегрирования уравнения в широком интервале температур.
Лекция№11
Летучесть (фугитивность).
Методы расчета летучести.
Уравнение состояния идеального газа используется для выражения через него различных функций, например, изобарно-изотермического потенциала при T=Const:
G = G0 + RT lnP, где G0 – константа интегрирования.
Чтобы получить аналогичную зависимость для реального газа необходимо выразить давление из уравнения Ван-дер-Ваальса, которое правильно описывает состояние реального газа только до давления 150-200 атмосфер. В технологических же процессах применяются давления до 40 тыс. атмосфер, следовательно, уравнение Ван-дер-Ваальса не применимо. В таком случае используют эмпирическое уравнение состояния:
PV = RT + aP + bP2 + cP3 + ….., где а, b, c – вариальные коэффициенты.
Их может быть до нескольких десятков, что приводит к громоздким выражениям термодинамических потенциалов.
Для устранения этой трудности Льюис предложил использовать метод летучести, суть которого заключается в том, что для характеристики реальных газов используются простые т/д выражения, но давления в них заменяются летучестью.
G = G0 + RT lnf, где lim (f/P) = 1 при Р →0
Летучесть – такое давление, которое должен был бы иметь реальный газ, если бы его свойства можно было бы описать с помощью уравнений идеального газа.
Для характеристики степени отклонения давления газа от идеального вводят понятие коэффициент летучести (γ).
γ =  при Р = 0, γ = 1
при Р = 0, γ = 1
С введением понятия летучести возникает необходимость нахождения зависимости f от P и f от Т. Наибольшее значение имеют два метода расчета летучести:
а) графический, согласно уравнению 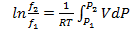 , в котором интеграл находят графическим методом;
, в котором интеграл находят графическим методом;
б) аналитический, основанный на принципе соответствующих состояний. Согласно этому принципу, ряд одинаковых свойств, в том числе и коэффициент летучести различных реальных газов, оказывается равным при одинаковых значениях приведенной температуры t и приведенного давления p. Значения g при различных p и t можно определить, пользуясь справочными таблицами «Коэффициенты активности реальных газов» или диаграммой.
Приведенной температурой и приведенным давлением называются соответственно отношения абсолютной температуры и давления к их критическим значениям (справочные величины):
 и
и