Из I-го закона т/д нельзя сделать вывод о возможности самопроизвольного протекания процесса. Поскольку все реальные процессы протекают в определенном направлении, то для изменения направления необходимо изменить условия протекания процессов. Все реальные процессы не являются равновесными и протекают с конечной скоростью, приближая систему к равновесию. В момент наступления равновесия процесс заканчивается.
Неравновесный процесс, протекающий в направлении достижения равновесия без воздействия внешних условий, называется самопроизвольным (положительным).
Обратный по направлению процесс, который не может протекать без внешних воздействий и удаляющий систему от равновесия называется несамопроизвольным (отрицательным).
II закон термодинамики позволяет предсказать направление протекания процесса. Он имеет несколько формулировок:
Постулат Клаузиуса
Единственным результатом любой совокупности процессов не может быть переход теплоты от менее нагретого тела к более нагретому.
Постулат Томсона
Теплота наиболее холодного из участвующих в процессе тел не может служить источником работы. (Теплота не может полностью перейти в работу).
3.
Вечный двигатель второго рода невозможен, т.е. невозможно построить такую машину, которая производила бы работу за счет тепла окружающей среды, не более нагретой, чем сама машина.
Т.о., процесс превращения теплоты в работу является несамопроизвольным и для его проведения необходима специальная организация такого процесса (паровая машина).
Пусть Т1 – температура нагревателя, Т2 – температура холодильника. Пусть имеется цилиндр с поршнем и некоторым количеством вещества, которое называется рабочим телом (например, пар). Оно совершает циклическую последовательность процессов, периодически возвращаясь в исходное состояние. КПД такой машины - отношение совершенной работы к затраченной теплоте: η = 
Итальянский ученый Карно рассмотрел идеальную тепловую машину, в которой рабочим телом является 1 моль идеального газа, а все процессы совершаются идеально равновесно.
ηидеальн = 
В идеальной машине Карно совершается максимальная работа, однако КПД составляет лишь около 40%, т.к. невозможно достичь температуры холодильника 0К. В реальной тепловой машине совершается меньшее количество работы и КПД существенно ниже.
Энтропия
Энтропия – функция состояния термодинамической системы, используемая во втором законе т/д для выражения через нее возможности или невозможности самопроизвольного протекания процесса (введена Клаузиусом).
Изменение энтропии определяется отношением количества теплоты, сообщенного системе или отведенного от нее, к температуре системы:
,
где знак равенства относится к равновесному процессу, неравенства – к неравновесному. Т.о. в равновесном процессе:
DS = 
.
По изменению энтропии в изолированной системе можно предсказать т/д возможность протекания самопроизвольного неравновесного процесса. Если энтропия увеличивается (DS > 0), то самопроизвольный неравновесный процесс возможен, если DS < 0 – невозможен. Т.о. все самопроизвольные процессы в изолированных системах идут в сторону увеличения энтропии до достижения равновесия, где она будет иметь постоянное и максимальное значение.
Вычисление изменения энтропии в различных процессах
Изменение энтропии в сложной системе или сложном процессе складывается из изменений ее в отдельных частях системы или в отдельных стадиях процесса, т.е.
DS1+2 = DS1 + DS2.
Абсолютное значение энтропии вещества при любой температуре можно рассчитать, если известна абсолютная величина энтропии при какой-либо температуре Т1, к которой прибавляется величина DS, обусловленная превращениями, происходящими при изменении температуры до величины Т2:
S2 = S1 + DS.
Изменение энтропии, в зависимости от условий, рассчитывается по следующим формулам:
1. Для идеального газа в небольшом температурном
интервале:
DS = n×(CV ln 
+ R ln 
)
DS = n×(CР ln 
+ R ln 
)
2. Для идеального газа в широком температурном
интервале:
DS = n×(
+ R ln 
)
DS = n×(
+ R ln 
),
где n – количество вещества,CР, Cv – мольные теплоемкости.
При Р = const: DS = n×CР ln 
или DS = n×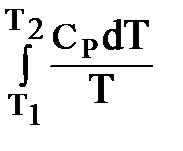 
;
При V = const: DS = n×Cv ln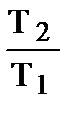 
или DS = n× 
При Т = const: DS = n×R ln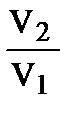 
= n×R ln 
3. При фазовых превращениях:
DSф.п. = 
,
где l - мольная теплота фазового превращения, т.е. теплота, необходимая для перехода 1 моль вещества из одного агрегатного состояния в другое; n – количество вещества, моль.
DSф.п. =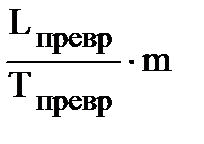 
,
где L - удельная теплота фазового превращения, т.е. теплота, необходимая для перехода 1 грамма вещества из одного агрегатного состояния в другое, m – масса вещества, г.
Мольная и удельная теплоты превращения связаны между собой:
lпревр. = Lпревр×М,
где М – молярная масса соединения.
Лекция № 8
Постулат Планка. Третий закон термодинамики.
Из II закона т/д можно определить только изменение энтропии. Абсолютное значение энтропии любого вещества в заданном агрегатном состоянии при любой температуре можно вычислить, используя постулат Планка:
Энтропия правильно построенного кристалла индивидуального вещества равна нулю при температуре абсолютного нуля (0 К).
S T =0 K= 0
Справедливость постулата подтверждается ходом эмпирических зависимостей теплоемкости от температуры, значения которых стремятся к нулю быстрее, чем сама температура. Для многих кристаллических веществ теплоемкость изменяется пропорционально кубу температур согласно уравнению Дебая, выведенному квантово-статистическим методом:
С = аТ3
Постулат Планка не выполняется для аморфных тел. Ввиду того, что постулат Планка позволяет рассчитать абсолютное значение энтропии, ему придается очень большое значение и ряд ученых предлагает считать его третьим законом термодинамики.
Таким образом, энтропия 1 моль любого вещества в твердом, жидком и газообразном состоянии при температуре Т и постоянном давлении соответственно равна:
SтвT,К =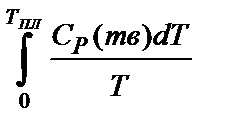 
,
SжидкT,К = 
+ 
+ 
+,
SгазT,К =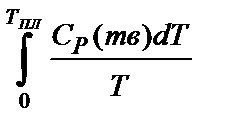 
+ 
+ 
+ 
+ 
,
где Ср - мольная теплоемкость.
Если вещество в твердом состоянии имеет несколько кристаллических модификаций, то в формулу добавляются слагаемые, обусловливающие нагревание первой модификации до температуры перехода во вторую, фазового перехода первой модификации во вторую и т.д.
Энтропия вещества в газообразном состоянии больше, чем в жидком, а в жидком – больше, чем в твердом. Поскольку жидкое вещество менее упорядочено, чем твердое, а газообразное вещество менее упорядочено, чем жидкое, это дало Больцману возможность характеризовать энтропию как меру беспорядка в системе.
Величина энтропии сложного образования отражает всю совокупность свойств системе вещества и зависит от молярной массы, агрегатного состояния, от кристаллического строения, изотопного состава и т.д.
