Завдання 1. 1-1. 12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь правильна. Оберіть правильну, на Вашу думку, відповідь та позначте її у бланку відповідей.

Варіант 1

Частина перша

Завдання 1.1-1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь та позначте її у бланку відповідей.

1.1. Якому одночлену дорівнює вираз 4a²b³ ^. 0,5ab²?

А) 2 а ³ b ⁶; Б) 2а²b⁶; В) 2а²b⁵; Г) 2 а ³ b ⁵.

1.2. При якому значенні у є правильною рівність √у = 0,4?

А) 0,4; Б) 1,6; В) 0,16; Г) 0,04.

1.3. Яка з пар чисел є розв'язком рівняння 4х - 3у = 1?

А) (1;1); Б) (7;-9); В) (2; -3); Г)(3;5).

1.4. Чому дорівнює добуток коренів рівняння х² -2х-5 = 0?

А) -5; Б) -2; В) 2; Г) 5.

1.5. Скільки автомобілів було на стоянці, якщо 36 з них було білого кольору, що становило усіх автомобілів?

А) 16; Б) 48; В) 54; Г) 81.

1.6. На рисунку зображено графік квадратичної функції

у = ах² +bх + с, дискримінант квадратного тричлена

ах ² +bх + с дорівнює D. Укажіть правильне твердження.

А) а > 0, с < 0, D > 0; В) а > 0, с > 0, D > 0;

Б) а < 0, с < 0, D > 0; Г) а < 0, с < 0, D < 0.

1.7. Басейн можна наповнити за 3 год, а злити з нього воду — за 5 год. Скільки часу знадобиться для наповнення басейну, якщо не закривати зливний отвір?

А) 7,5 год; Б) 8 год; В) 10,5 год; Г) 15 год.

1.8. Областю визначення якої функції є проміжок (9; + ∞)?

А) y = ; Б) y = ; B) y = ; Г) y = .

1.9. Укажіть хибне твердження.

А) косинус будь-якого гострого кута більший за косинус будь-якого тупого кута;

Б) косинус кута трикутника може дорівнювати нулю;

В) косинус кута трикутника може дорівнювати від'ємному числу;

Г) косинус кута трикутника може дорівнювати -1.

1.10. У колі з центром О, зображеному на рисунку, проведено хорду АВ, яка дорівнює радіусу кола. Через точки А і В проведено дотичні до кола, які перетинаються в точці С. Знайдіть кут АСВ.

А) 90°; В) 150°;

Б) 120°; Г) знайти неможливо.

1.11. У певний момент часу довжина тіні дзвіниці Софіївського собору (м. Київ) дорівнює 19 м, а довжина тіні ліхтарного стовпа, який стоїть біля дзвіниці, – 1,5 м. Яка висота дзвіниці, якщо висота стовпа дорівнює 6 м?

А) 76 м; Б) 72 м; В) 75 м; Г) 80 м.

1.12. Скільки осей симетрії має прямокутник, який не є квадратом?

А) жодної; Б) одну; В) дві; Г) чотири.

Частина друга

Розв'яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.

2.1. До 8 кг 60-відсоткового розчину солі долили 4 кг води. Яким після цього став відсотковий вміст солі в розчині?

2.2. Обчисліть суму п'яти перших членів геометричної прогресії (b_n), якщо

b₅ = 112, а знаменник прогресії q = 2.

2.3. Спростіть вираз – ^. ^.

2.4. Висота AD трикутника ABC ділить сторону ВС на відрізки BD і CD так, що BD = 15 см, CD = 5 см. Знайдіть сторону А С, якщо B = 30°.

Частина третя

Розв'язання задач 3.1 - 3.3 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання схемами, графіками, таблицями.

3.1. Не виконуючи побудови, знайдіть координати точок перетину графіків функцій y = і y = 5 – x. Накресліть графіки даних функцій і позначте знайдені точки.

3.2. Поїзд мав проїхати 64 км. Коли він проїхав 24 км, то був затриманий біля семафора на 12 хв. Тоді він збільшив швидкість на 10 км/год і прибув у пункт призначення із запізненням на 4 хв. Знайдіть початкову швидкість поїзда.

3.3. Основи рівнобічної трапеції дорівнюють 1 см і 17 см, а діагональ ділить її тупий кут навпіл. Знайдіть площу трапеції.

Варіант 2

Частина перша

1.1. Спростіть вираз (m - 3)(m+ 3)-m(m + 2).

А) - 2m - 9; Б) 9-2 m; В) 2m-9; Г) 2m+9.

1.2. Чому дорівнює значення виразу ?

А) 18; Б) 36; В) 54; Г) 108.

1.3. Яка область визначення функції у = ?

А) (4; + ); Б) (- ; 4]; В) (- ; 4); Г) [4; + ).

1.4. Виконайте множення: .

А) ; Б) ; В) ; Г) .

1.5. Число а менше від свого модуля. Укажіть правильне твердження.

А) а — невід'ємне число; В) а =0;

Б) а —додатне число; Г) а —від'ємне число.

1.6. Дерев'яну колоду розпиляли на дві колоди, довжини яких відносяться як 3:7. Яку частину даної колоди становить менша з отриманих колод?

А) ; Б) ; B) ; Г) .

1.7. Укажіть область значень функції, визначеної на проміжку [-2; 2], графік якої зображено на рисунку.

А)[-1;3]; Б) [-2; 2]; В)[1;3]; Г) [-2; 1].

1.8. Ціну товару спочатку знизили на 10 %, потім ще на

25 %, а через деякий час підвищили на 20 %. Як змінилася початкова ціна товару?

А) зменшилася на 15 %; В) зменшилася на 19 %;

Б) збільшилася на 10 %; Г) збільшилася на 12 %.

1.9. Скільки пар рівних трикутників зображено на рисунку?

А)1; Б) 2; В) 3; Г)4.

1.10. Чому дорівнює відношення площі круга до площі, вписаного в нього квадрата?

А) 2: ; Б) : 2; В) 4: ; Г) : 4.

1.11. Катети прямокутного трикутника дорівнюють 2 см і ? см. Знайдіть синус більшого гострого кута цього трикутника.

A) ; Б) ; В) ; Г)

1.12. Медіани трикутника ABC, зображеного на рисунку, перетинаються в точці М. Знайдіть коефіцієнт гомотетії з центром у точці М, при якій точка С₁ є образом точки С.

А) 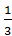; Б) ; В) - 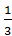; Г) - .

Частина друга

Розв'яжіть завдання 2.1 — 2.4. Запишіть відповідь у бланк відповідей.

2.1. Чому дорівнює значення виразу (2 - 7 - ) 2 ?

2.2. При яких значеннях b рівняння х² + bx +16 = 0 не має коренів?

2.3. Розв'яжіть систему рівнянь

2.4. 3 точки до прямої проведено дві похилі, проекції яких на пряму дорівнюють 5 см і 9 см. Знайдіть відстань від даної точки до цієї прямої, якщо одна з похилих на 2 см більша за другу.

Частина третя

3.1. Доведіть, що при a -1 виконується нерівність а ³ +1 а ² + а.

3.2. Катер пройшов 30 км за течією річки і повернувся назад, витративши на весь шлях 2 год 15 хв. Визначте швидкість течії, якщо власна швидкість катера дорівнює 27 км/год.

3.3. Сторони трикутника дорівнюють 6 см і 8 см. Медіана трикутника, проведена до його третьої сторони, дорівнює см. Знайдіть невідому сторону трикутника.

Варіант 3

Частина перша